РВСС Распространение волн в случайных средах / Лекции / New Асимптотика УПИ степенные индикатрисы

Асимптотика малоуглового уравнения переноса

(глубинный режим )

Уравнение Шрёдингера с «мнимым» временем

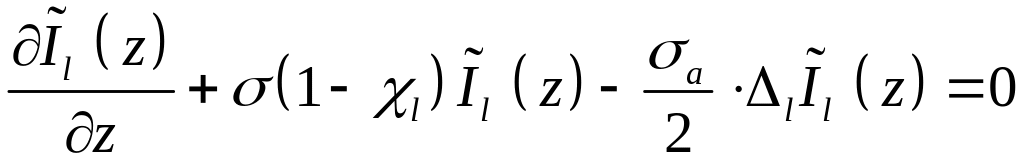
Задача на собственные значения

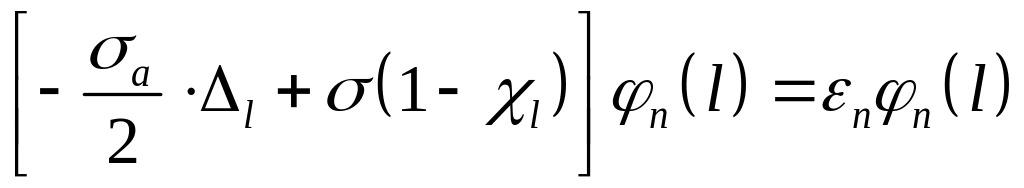
Разложение модифицированной интенсивности по собственным функциям

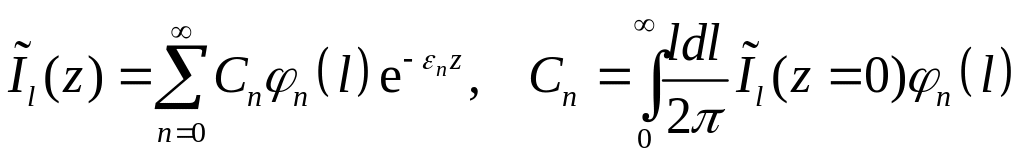
В глубинном режиме

Пространственно-угловое представление

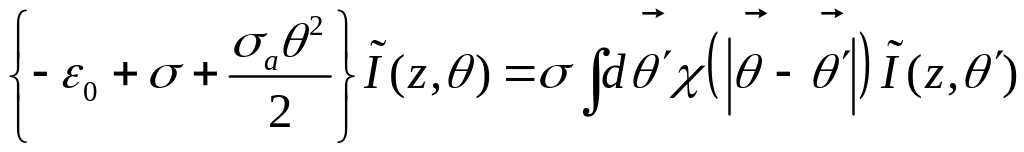
Закон сохранения полного потока ( )

Или

Угловая зависимость интенсивности на «крыльях» в асимптотическом режиме

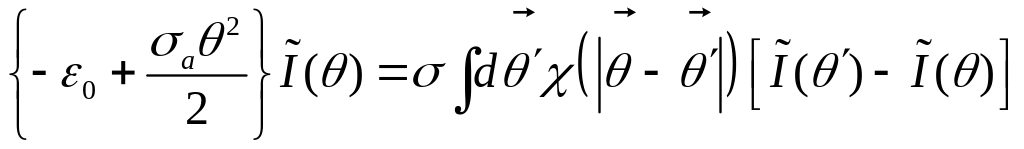
Оценка слагаемых при

Уравнение переноса в угловом представлении

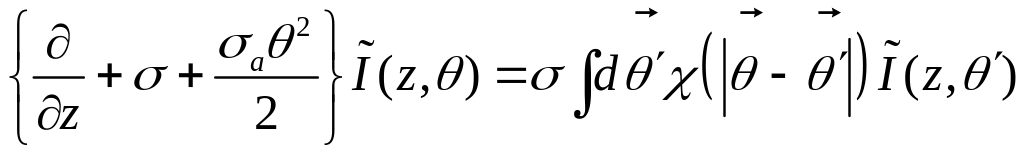
Третье слагаемое в левой части приводит к появлению экспоненты:

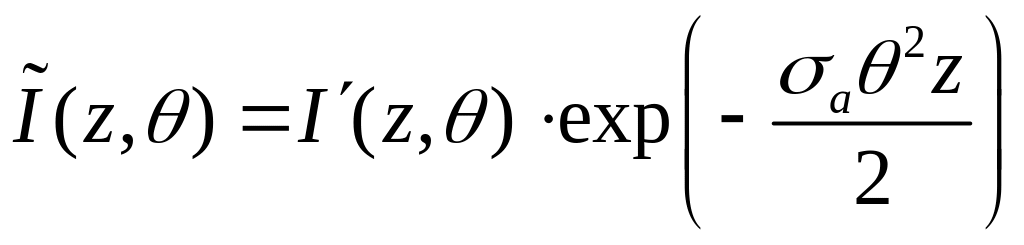
Поглощение начинает сказываться на углах отклонения

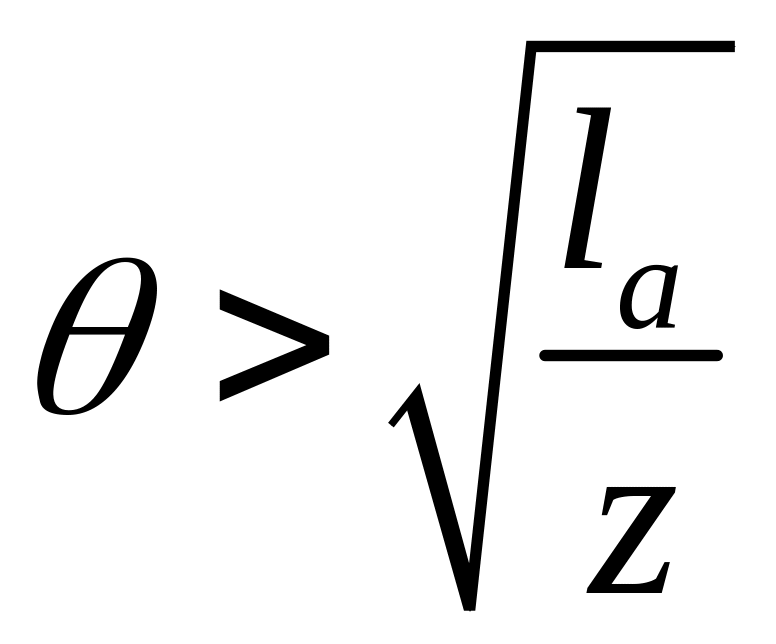
Отношение

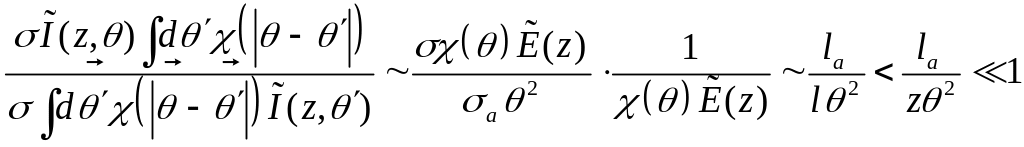
Если , то отношение

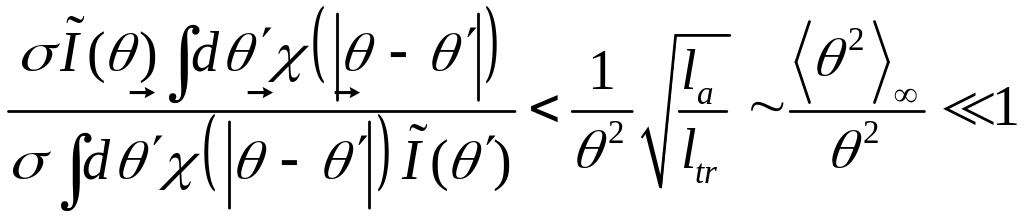
Результат:

Или

(*)

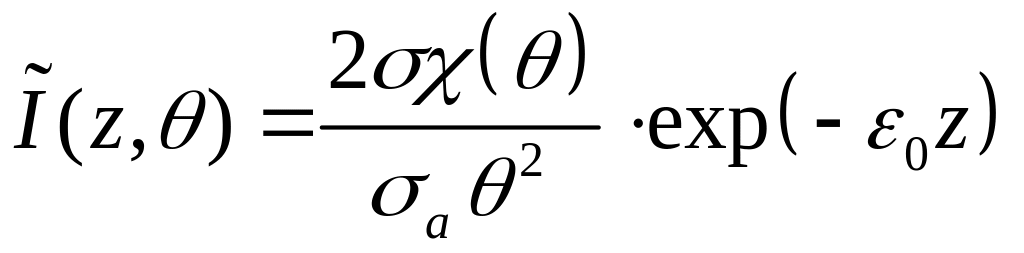Индикатрисы Рейнольдса- Маккормика

(Reynolds L and McCormick N J 1980 JOSA A 70 1206)

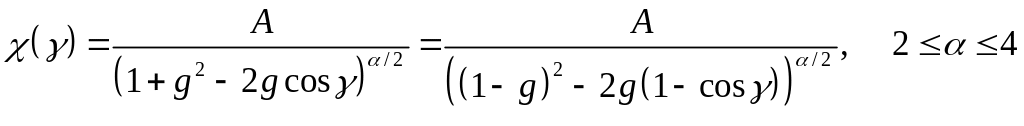
Резко анизотропное рассеяние

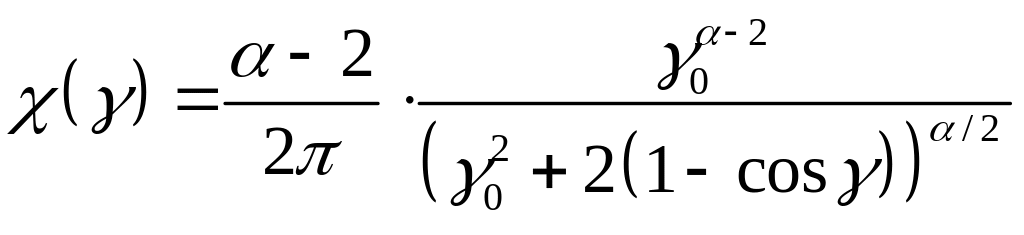
Транспортное сечение

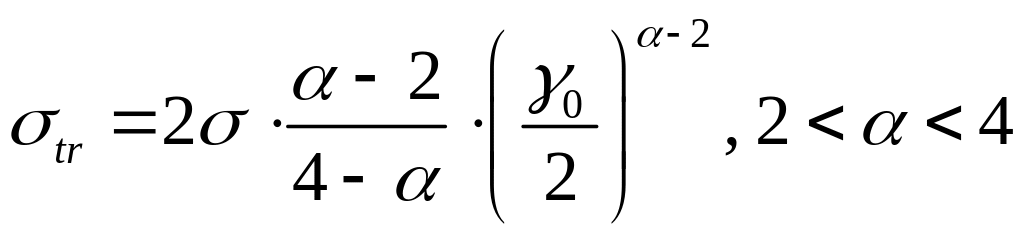
Малоугловое приближение

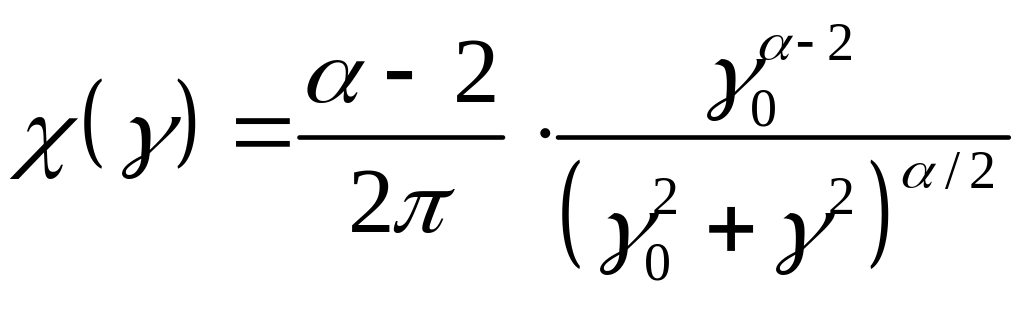
Найти асимптотику в области

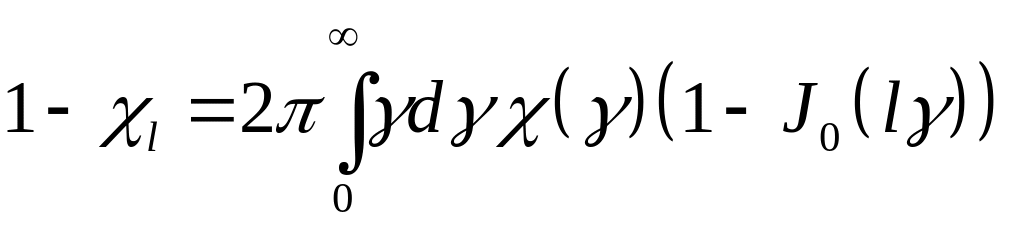
Табличный интеграл

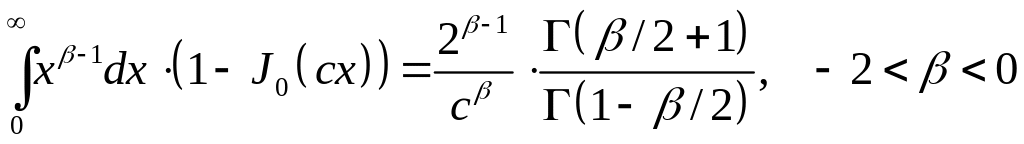
«Потенциал»

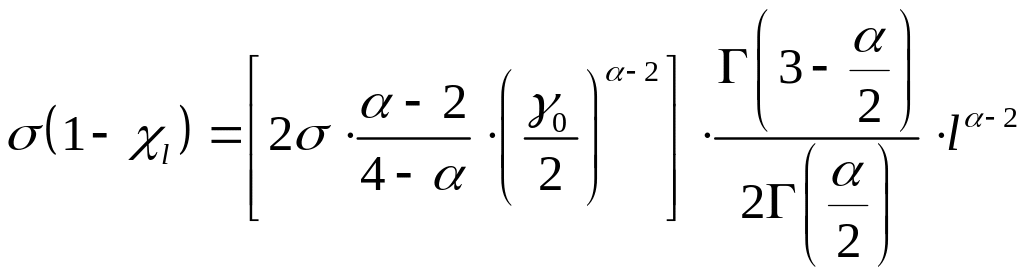
«Уравнение Шрёдингера» для степенных индикатрис

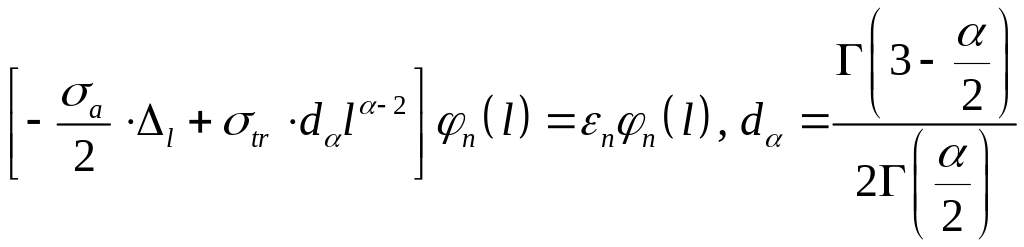
«Потенциал»

Вариационный метод ( )

Минимум функционала

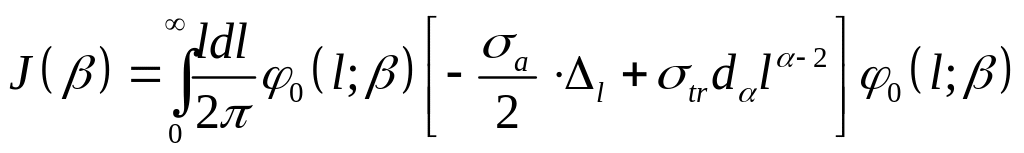
Пробная функция – из результатов приближения диффузии по углам

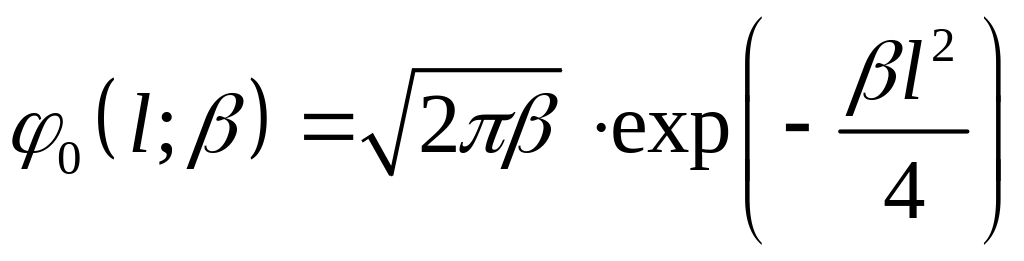
Физический смысл ?

Промежуточные формулы

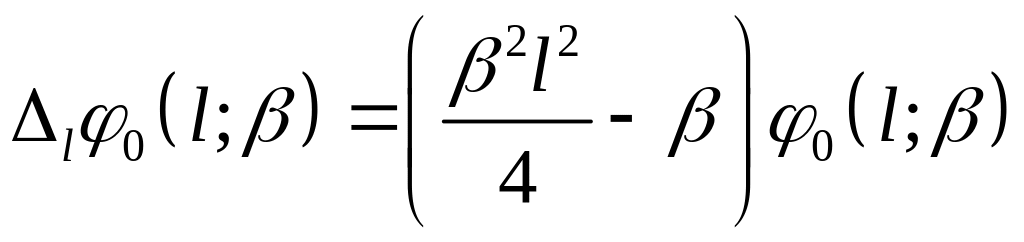
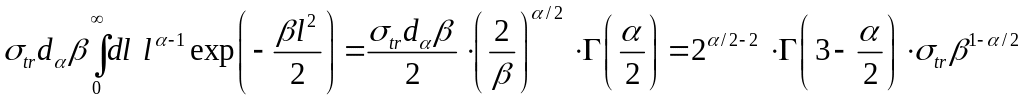
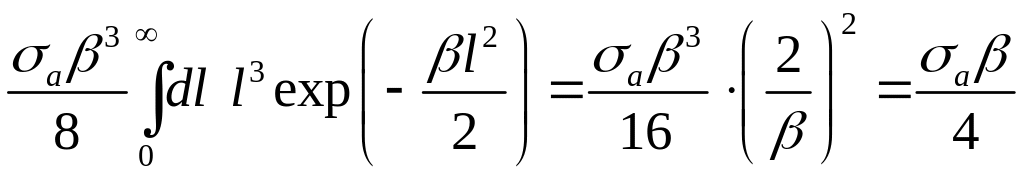
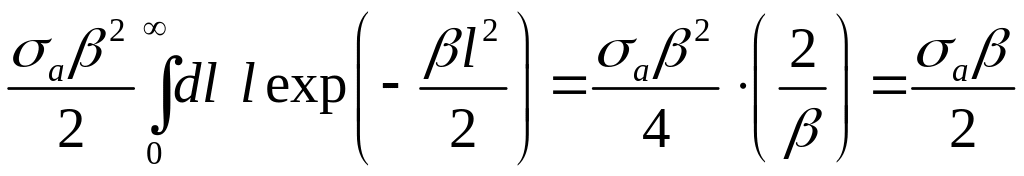
Функционал

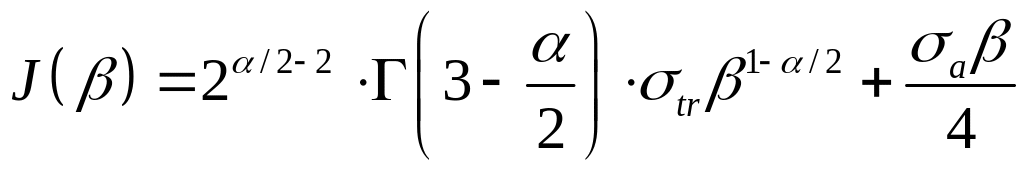
Минимум функционала

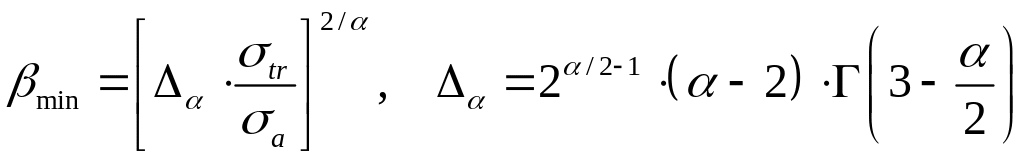
Приближение диффузии по углам ,

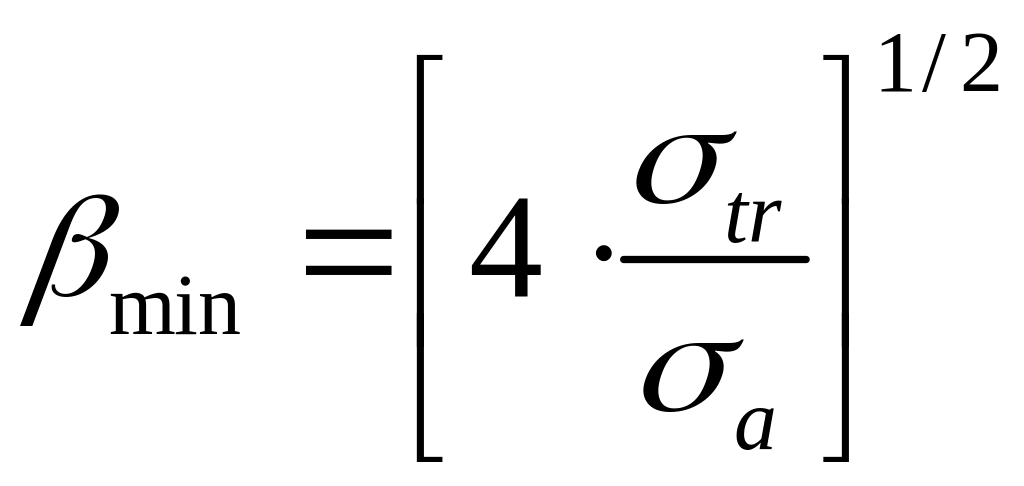
Собственное значение

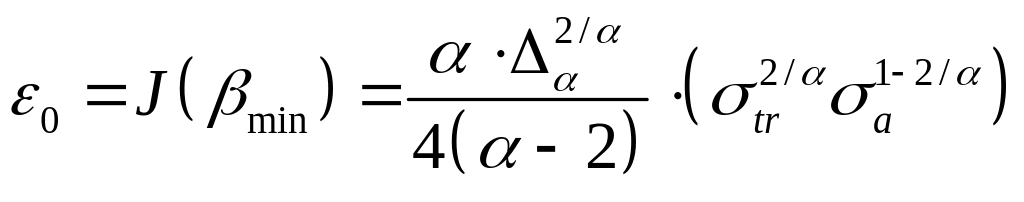
Приближение диффузии по углам ,

Автомодельность решения

Вспоминаем малоугловую диффузию

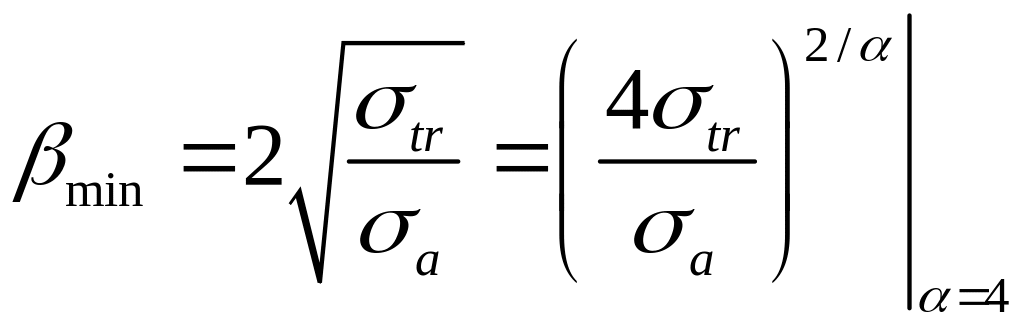
Введём новую переменную

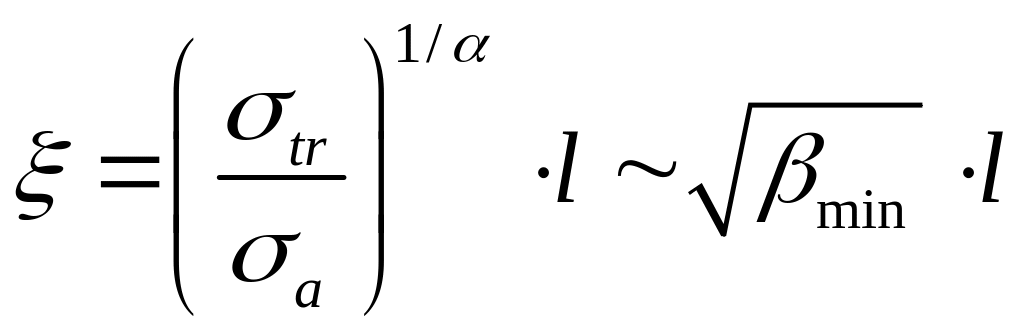
Преобразуем исходное уравнение

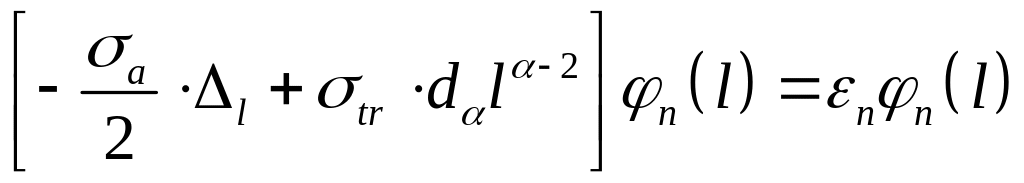
Результат

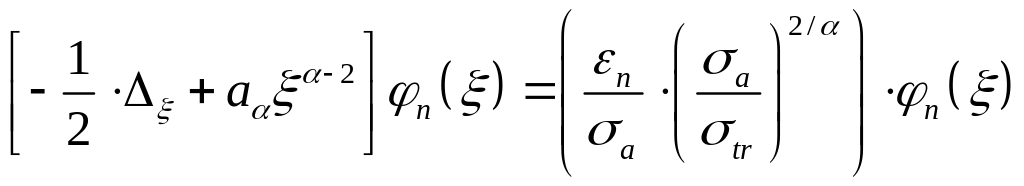
Собственные значения

где - безразмерные собственные значения!

Ми-частицы в поглощающей матрице

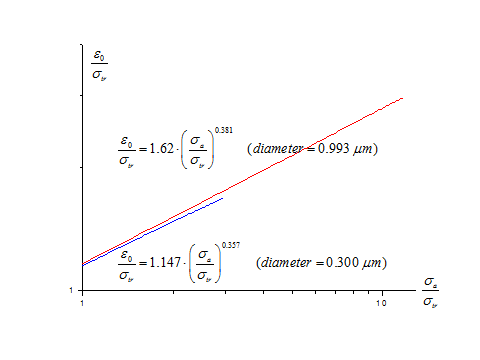
Зависимость формы углового распределения от оптических характеристик среды.

Слабое поглощение

Тонкий слой - угловое распределение резко анизотропное.

Убывание на «крыльях» распределения по закону однократного рассеяния (для степенных индикатрис).

Толстый слой - режим пространственной диффузии, угловое распределение изотропное.

Сильное поглощение , угловое распределение для любой толщины слоя всегда резко анизотропное

Тонкий слой :

- убывание углового распределения по закону однократного рассеяния

- убывание углового распределения по закону

Толстый слой - асимптотический режим:

- убывание углового распределения по закону