РВСС Распространение волн в случайных средах / Лекции / Интенсивность в импульсе

gorodn@theor.mephi.ru

Временной профиль интенсивности

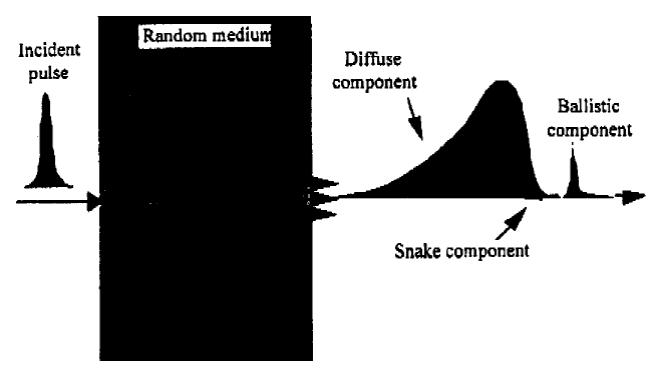
Уравнение переноса интенсивности широкого импульсного сигнала

Приведение к стационарному УПИ с помощью преобразования Фурье

«Пороговое» время, отделяющее “snake”-фотоны от диффузионной составляющей:

Транспортное время

“Snake”-фотоны

Выделяем «тривиальное» поглощение – вводим модифицированную интенсивность

Уравнение для модифицированной интенсивности

Удобно ввести новые переменные

- разница между длиной пути фотона и толщиной (запаздывание)

Уравнение переноса в новых переменных

Приближение малых углов

Преобразования Лапласа+Бесселя

Уравнение для

Интенсивность в импульсе в приближении Фоккера-Планка (диффузия по углам)

Уравнение Фоккера-Планка для Лаплас-образа

Лаплас-образ

Угловое распределение в импульсе (*)

Напрашивается безразмерная переменная

Переписать интеграл!

Угловое распределение в импульсе (**)

Или

- универсальная функция!

“Snake”-фотоны – малые запаздывания или . Основной вклад в интеграл по даёт область . Т.е.

Оценить этот интеграл методом перевала!

Ответ

Вспомогательные вычисления

Точка экстремума

Вблизи точки экстремума

Искомый интеграл

Наконец, сдвигаем контур интегрирования: .

Средний квадрат угла многократного рассеяния в приближении Фоккера-Планка

Уравнение для

Первый шаг

Вычислить модифицированную освещённость в приближении Фоккера-Планка!

- универсальная функция.

Второй шаг

Вычисление , используя автомодельность решения.

Наводящие соображения: производная

Попытаемся свести второе слагаемое

к производной !

Предположим, что

.

Получить уравнение для !

Ответ

Условие применимости приближения малых углов в импульсе

или или

Угловое распределение интенсивности в импульсе

Универсальная функция под «куполом» ( )

Временная зависимость интенсивности в импульсе под «куполом»

Момент достижения максимума интенсивности в импульсе при .

Или

Вывод: при толщине образца (слой может быть толстым!) максимум интенсивности в импульсе наблюдается в малоугловом режиме распространения!

Поглощающая среда

Момент достижения максимума интенсивности в импульсе при .

Большие толщины ?

Или

Средний квадрат угла многократного рассеяния для степенных индикатрис Рейнольдса-Маккормика

Собственные значения

Уравнение для

Модифицированная освещённость

Величины - безразмерные (см. граничное условие для )

Поэтому

Или

где - универсальная функция

Вычисление среднего квадрата .

Наводящие соображения: производная

Попытаемся свести второе слагаемое

к производной !

Предположим, что

.

Получить уравнение для !

Ответ

Интенсивность в импульсе в пренебрежение флуктуациями длин пробегов фотонов (приближение Мольер)

Непоглощающая среда

Ищем решение УПИ в виде интеграла Фурье

Найти решение!

Решение

(CW) - continuous-wave scattering

Отсутствует временное расплывание импульса за счёт рассеяния!

November 1, 1990 / Vol. 15, No. 21 / OPTICS LETTERS

Time-resolved transillumination for medical diagnostics

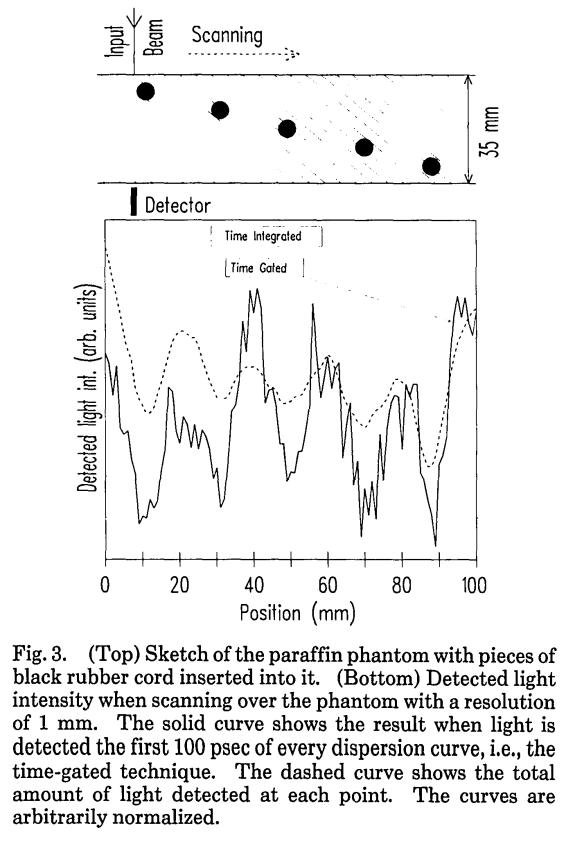
Рис.4. Интенсивность в зависимости от положения оси системы источник-детектор. Экспериментальные результаты показаны символами. Сплошная кривая описывает наши расчёты с фазовой функцией Хеньи-Гринстейна для соответствующей системы полностью поглощающих полос. Толщина образца , транспортная оптическая толщина . Начало детектирования совпадает со значением времени пролёта , длительность интервала детектирования .

Диффузионная составляющая импульса

Исходное УПИ ( )

Уравнение для гармоник

P₁ – приближение

Почти изотропное рассеяние – оставляем только слагаемые с

Получить уравнение диффузии для !

Промежуточная формула

Оценка:

Уравнение для

Уравнение диффузии плотности энергии излучения в импульсе

- коэффициент диффузии.

Точечный источник в бесконечной среде

Решение

Полубесконечная среда

Граничное условие

Плотность энергии излучения от источника, расположенного в точке

Литература по диффузии в импульсе

И.Н. Минин, Теория переноса излучения в атмосферах планет, Москва, Наука, 1988.