РВСС Распространение волн в случайных средах / Лекции / Импульс-уравнение БС

Уравнение Бёте-Солпитера

Интегральные уравнения для функций Грина

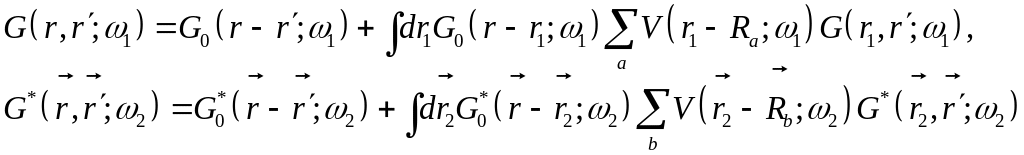
Символическая запись

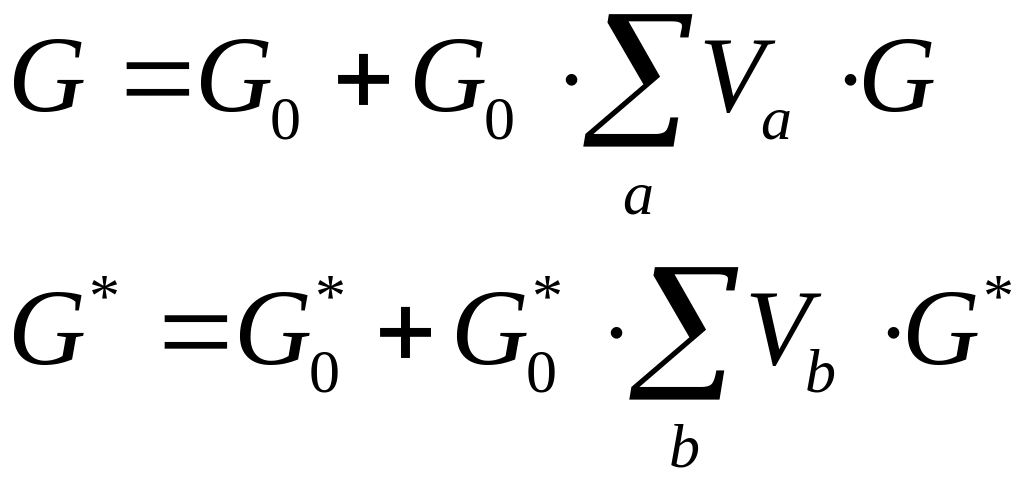
Первая и вторая итерации

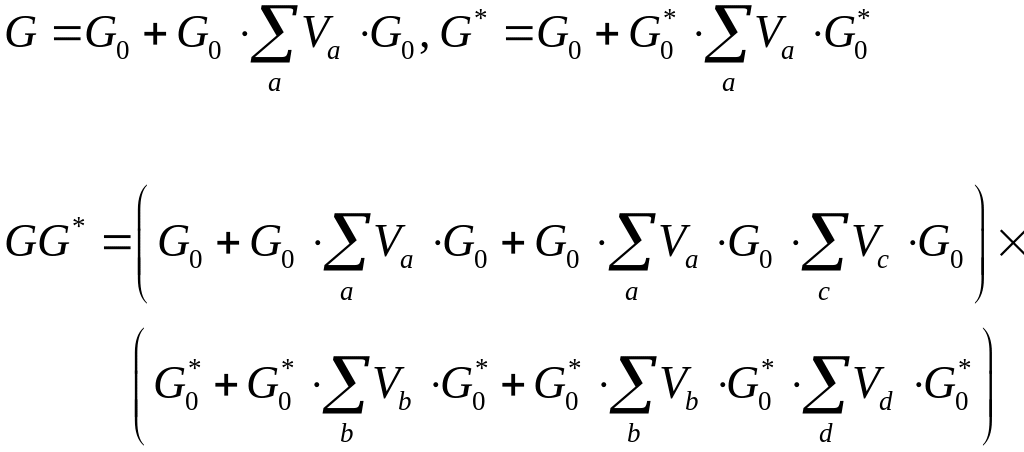
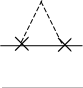
Сильно и слабо связанные диаграммы

Графическое уравнение Бёте-Солпитера

Оператор интенсивности – сумма всех сильно связанных диаграмм

Уравнение Бёте-Солпитера в явном виде

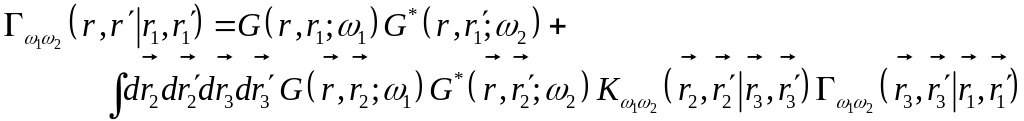
Приближение слабой локализации

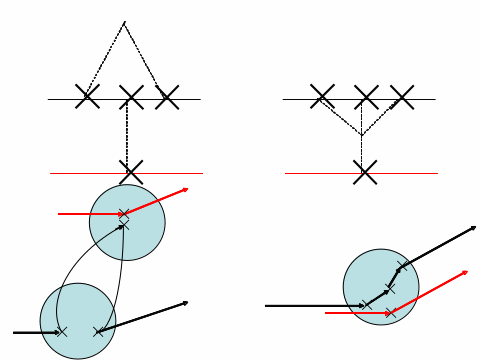
Оператор интенсивности в приближении слабой локализации

Уравнение Бёте-Солпитера для матрицы плотности в приближении слабой локализации

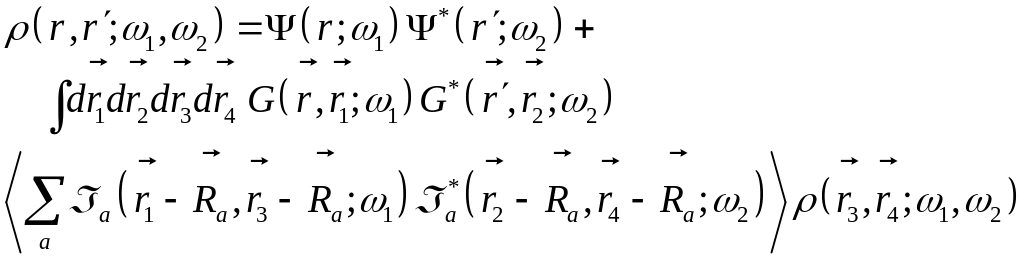
Или

План преобразования уравнения Б-С:

1. Пренебрегаем эффектами Френелевского преломления и отражения волн на границе среды, т.е.

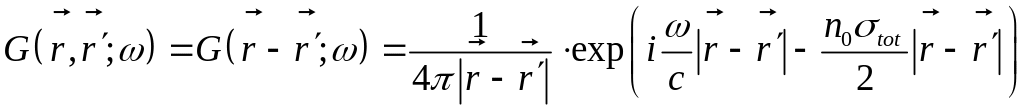
2. Сделаем замену переменных

3.Сделаем приближение дальней зоны в функциях Грина

4. Разложим матрицы рассеяния в интегралы Фурье

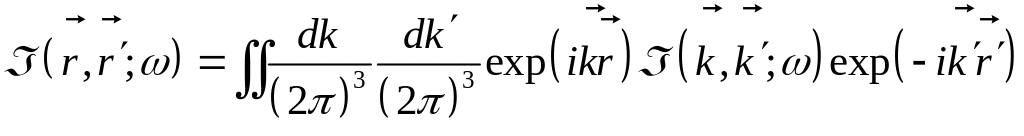
5. Запишем матрицу плотности в представлении Вигнера

В результате?

Промежуточная формула

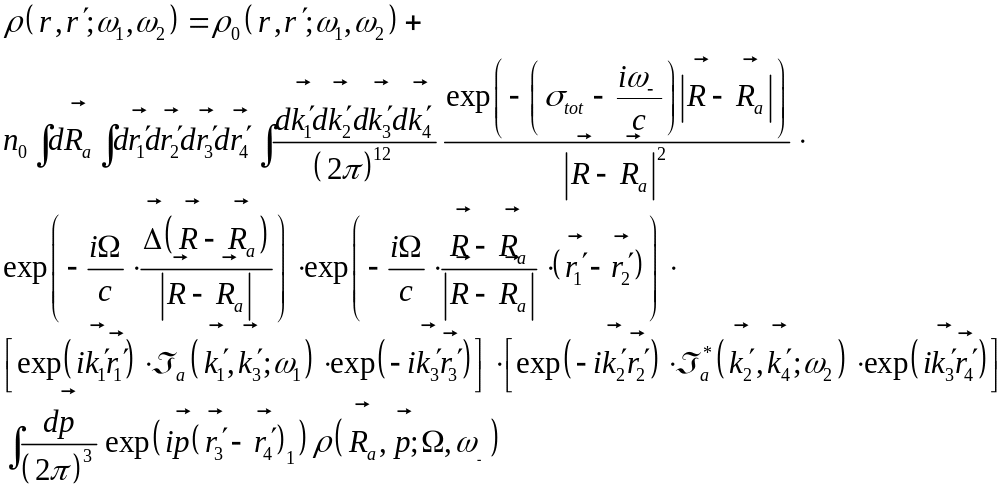
Уравнение переноса в интегральной форме

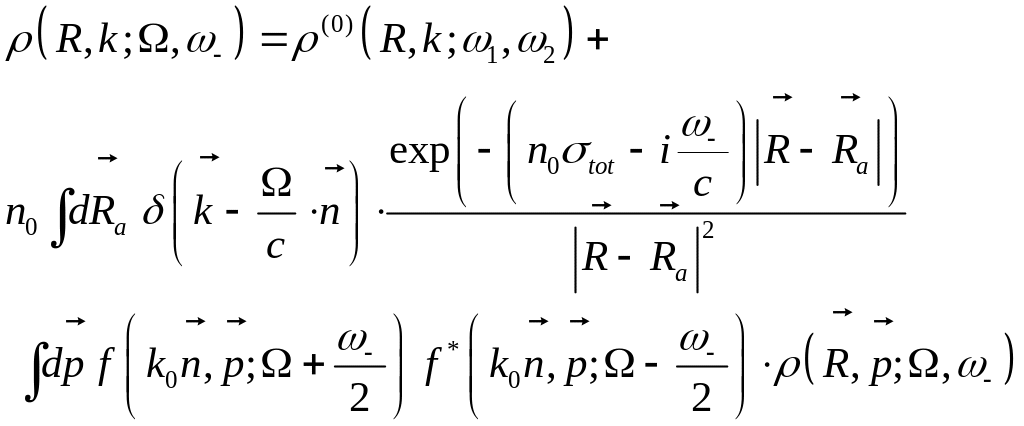
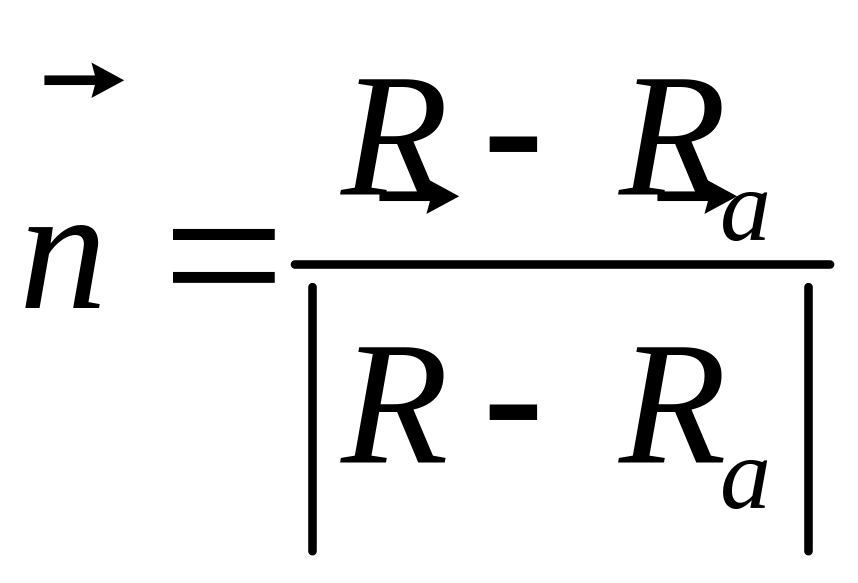
Вспоминаем, что

Поэтому ищем решение в виде

Уравнение для ?

Уравнение переноса в интегральной форме

«Укороченное» уравнение переноса (для нерассеянного излучения)

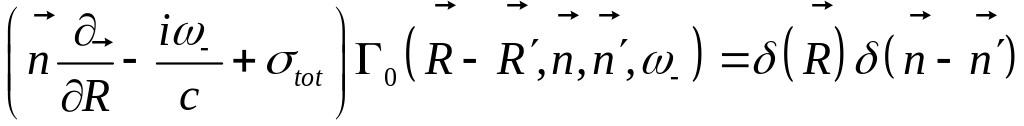
Функция Грина

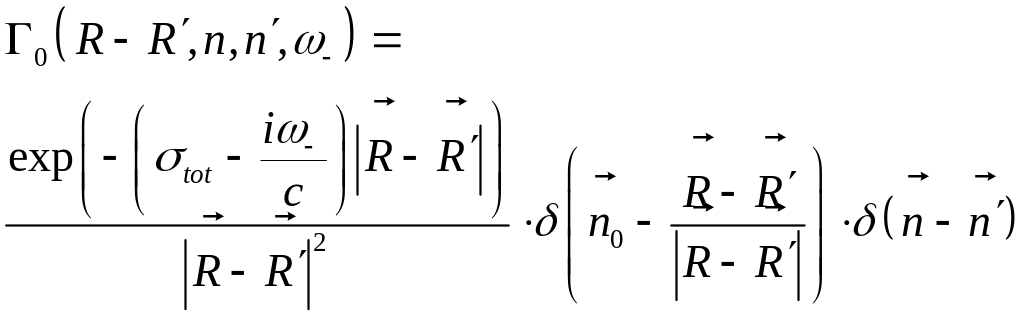
Получить интегро-дифференциальное уравнение переноса излучения в импульсе?

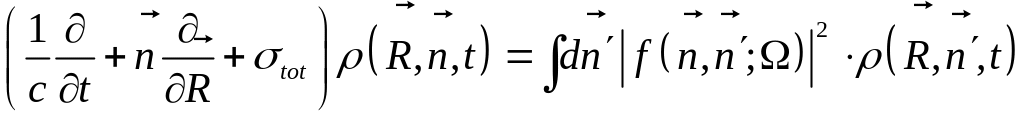
В случае распространения частиц отсутствие рассеивателей ( ) левая часть уравнения переноса представляет из себя закон сохранения

Литература

А. Исимару, Распространение и рассеяние волн в случайно-неоднородных средах, т.1,2, Мир,Москва (1981).