лабы / 9_Multisim_Езеров / Multisim_метода
.pdf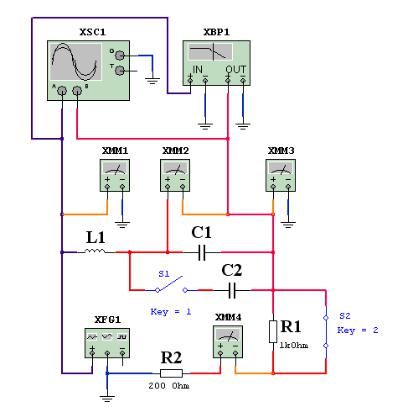
Лаб.раб.7_резонанс_напряжений.ms7 схему для исследования последовательного контура (рис. 7.3).
Рис. 7.3
В открывшемся окне появится схема RLC -цепи с подключенными к ней измерительными приборами. Для питания цепи применяется генератор синусоидального напряжения XFG1, амплитуда напряжения которого устанавливается Um = 2,828 В (т. е. U = 2 В). Частота источника напряжения
задается дискретно с клавиатуры компьютера f = 2...30 кГц. Напряжения
измеряют вольтметрами XMM1 – XMM3, а тока – амперметром XMM4. Осциллограммы входного напряжения и напряжения на сопротивлениях, пропорционального току, снимаются двухканальным осциллографом XSC1. Для получения графиков частотных характеристик используется плоттер ХВР1.
Схемы для исследования резонанса в контурах с малыми потерями, с большими потерями и с дополнительной емкостью собираются с использованием ключей S1 и S2, которые переключаются клавишами 1, 2 соответственно с клавиатуры. Визуализация виртуальных изображений лицевых плат приборов осуществляется двумя щелчками левой клавиши мыши при установке курсора на изображение прибора.
61
7.2.1. Исследование резонанса напряжений и АЧХ контура с малыми
потерями |
|
Активизируйте схему (рис. 7.3) с помощью кнопки |
на панели |
инструментов. Соберите с помощью ключей S1 и S2 цепь, изображенную на |
|
рис. 7.4 ( L1 = 25 мГн, C1 = 0,005 мкФ, R2 = 200 Ом), где |
вольтметр и |
амперметр условно показывают место измерения значений. Потери в контуре объясняются неидеальностью его элементов и характеризуются
сопротивлением потерь |
R2 , так что в данном случае в цепи |
на рис. 7.1, а |
||||||||||||||||||
R = R2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
Исследуйте |
|
|
частотные |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
характеристики |
RLC -контура |
с |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
помощью плоттера ХВР1, открыв его |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
экран двойным |
щелчком |
мыши |
по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
u(t) |
|
|
|
|
R |
|
|
|
|
|
С1 изображению |
прибора. |
Нажмите |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
кнопку Reverse, чтобы получить белый |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фон экрана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.4
Для снятия ФЧХ входной проводимости контура нажмите кнопку Phase на верхней панели Mode плоттера. На левой панели управления Horizontal установите диапазон частот измерения ФЧХ: Lin (шкала горизонтальной оси линейная); начальное ( I) 10 кГц и конечное ( F) 20 кГц значения частот, устанавливаемых по горизонтальной оси. На правой панели управления
Vertical установите аналогично линейный масштаб Lin; начальное ( I = 90 ) и конечное ( F = −90 ) значения ФЧХ. Определите резонансную частоту f0
контура при значении ФЧХ ноль градусов с помощью курсора на экране плоттера. Курсор перемещается мышью. Значения частоты и фазы выводятся внизу информационного поля. Результат измерения занесите в табл. 7.1.
|
|
|
|
|
|
|
|
Таблица 7.1 |
|
|
|
|
|
|
|
|
|
|
|
|
Измеряют при резонансе |
|
|
Вычисляют |
|||||
|
|
|
|
|
|
|
|
|
|
U, В |
|
I, мА |
f0 , кГц |
UС1 , В |
R, Ом |
Q |
ρ, Ом |
L, Гн |
C, мкФ |
|
|
|
|
|
|
|
|
|
|
62
Для исследования АЧХ входного сопротивления контура нажмите кнопку Magnitude на верхней панели Mode плоттера. Установки масштаба по горизонтали такие же, как при исследовании ФЧХ, а на правой панели управления Vertical установите линейный масштаб отношения напряжений
на выходе и входе Lin, начальное ( I) 1 m (10−3 ) и конечное ( F) 1 значения АЧХ. Установите курсор на резонансную частоту f0 контура, которая
соответствует максимальному значению АЧХ. Определите по графику АЧХ
граничные частоты полосы пропускания контура на уровне 0,707 |
|
Ymax |
|
и по |
|
|
|||
формуле (7.11) найдите добротность контура. |
|
|
||
Установите на источнике найденную резонансную частоту |
|
f0 , |
||
проверьте ее по осциллографу XSC1 и измерьте ток I и напряжения на входе U , на емкостном элементе UC1 и на сопротивлении UR . Для этого
произведите визуализацию виртуальных изображений лицевых плат приборов XMM1 – XMM4 двумя щелчками левой клавиши мыши по изображениям этих приборов. Показания амперметра и вольтметров запишите в табл. 7.1.
По данным измерений вычислите R , Q , ρ, L , C , сравните значение добротности с вычисленным по (7.11).
Для определения зависимости входной проводимости RLC -контура от частоты измеряйте ток, изменяя частоту через 1 кГц в диапазоне 9…12 кГц, через 0,2 кГц – в диапазоне 12…16 кГц и далее снова через 1 кГц в диапазоне
16…20 кГц. Результаты |
измерений занесите в табл. |
7.2, в |
которую |
||||||||
|
|
|
|
|
|
|
|
|
|
Таблица 7.2 |
|
|
|
|
|
|
|
|
|
||||
|
Измеряют |
|
Вычисляют |
|
|
|
|||||
|
f, кГц |
|
I, мА |
|
|
Y ( jω) |
|
, См |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
необходимо перенести также значение тока I при f = f0 из табл. 7.1. |
|||||||||||
По данным табл. 7.2 постройте график АЧХ последовательного контура. |
|||||||||||
7.2.2. Исследование |
резонанса |
напряжений и |
|
АЧХ |
контура |
||||||
с большими потерями
Соберите схему, изображенную на рис. 7.5. Потери в этом контуре определяются сопротивлением R = R1 + R2 . Методика исследования здесь
такая же, как в 7.2.1. Результаты измерений занесите в таблицы, аналогичные
табл. 7.1 и 7.2. Поскольку АЧХ цепи является более плавной,
63
R L1
u(t) |
C1 |
Рис. 7.5
рекомендуется в диапазонах 8…12 кГц и 16…20 кГц изменять частоту через 2 кГц. По результатам измерений в табл. 7.1 вычислите лишь R и Q . Постройте АЧХ аналогично 7.2.1.
7.2.3. Исследование влияния емкости на характеристики контура
Соберите цепь, изображенную на рис. 7.6.
R L1
C1 
С2
u(t)
Рис. 7.6
Проведите измерения, аналогичные 7.2.2, изменяя частоту в диапазонах 1…5 и 9 …15 кГц через 1 кГц, а в диапазоне 5 …9 кГц через 200 Гц. Заполните таблицы, аналогичные табл. 7.1 и 7.2.
Проведите аналогичные расчеты и построения графиков.
7.3. Исследование резонанса токов с применением компьютерных программных средств Multisim
Загрузить из файла Лаб.раб.7_резонанс_токов_last.ms7 схему для исследования параллельного RLC -контура (рис. 7.7).
В открывшемся окне появится схема параллельного RLC -контура с подключенными к ней измерительными приборами. Для питания цепи используется источник синусоидального тока I1, параметры которого задаются в диалоговом окне, открываемом двойным щелчком левой клавиши
мыши по изображению источника. Амплитуда тока Current (Pk)
64
устанавливается |
Im =1,4142 мA, при |
этом действующее значение тока |
|
источника |
I =1 |
мA. Частота источника тока Frequency (F) задается |
|
дискретно с |
клавиатуры компьютера |
f = 2...30 кГц. Напряжение в цепи |
|
измеряется вольтметром XMM2, а токи – амперметрами XMM1, XMM3. Для снятия частотных характеристик используется плоттер ХВР1.
Рис. 7.7
Схемы для исследования резонанса в контурах с малыми потерями, с большими потерями и с дополнительной емкостью собираются с использованием ключей S1 и S2, которые переключаются с клавиатуры цифрами 1, 2 соответственно. Визуализация виртуального изображения лицевых плат приборов осуществляется двумя щелчками левой клавиши мыши при установке курсора на изображение прибора.
7.3.1.Исследование резонанса токов и АЧХ параллельного контура
смалыми потерями
Соберите схему ( R1 = 20 кОм; L1 = 25 мГн; C1 = 0,005 мФ), изображенную на рис. 7.8.
|
|
C1 |
i(t) |
R1 |
L1 |
Рис. 7.8
65
Потери в цепи объясняются неидеальностью элементов и могут характеризоваться проводимостью потерь R1, так что в данном случае в цепи
на рис. 7.1, б имеем G =1
R1 .
Кнопкой 
на панели инструментов активируйте цепь. Исследуйте частотные характеристики RLC -контура с помощью плоттера ХВР1, визуализировав изображение двойным щелчком мыши по изображению плоттера. Нажмите кнопку Reverse, чтобы получить белый фон изображения. Исследуйте ФЧХ входного сопротивления контура в диапазоне частот f =10...18 кГц, установив параметры плоттера аналогично 7.2.1. Определите
резонансную частоту f0 контура при скачке ФЧХ. Результат измерения
занесите в табл. 7.3.
Исследуйте аналогично 7.2.1 в том же диапазоне частот АЧХ входного сопротивления контура. Определите полосу пропускания и добротность. Установив на источнике тока I1 резонансную частоту f0 , измерьте
параметры, указанные в табл. 7.3.
|
Таблица 7.3 |
|
|
Измеряют при резонансе |
Вычисляют |
I, мА U 0 , В f0 , кГц IC0 , мА Q G, См |
R =1 G , Ом ρ, Ом L, Гн C, мкФ |
Для получения АЧХ (зависимости входного сопротивления от частоты) измеряйте напряжение, изменяя частоту через 1 кГц в диа пазоне 8…12 кГц, через 0,5 кГц в диапазоне 12…16 кГц и далее снова через 1 кГц в диапазоне 16…20 кГц. Результаты измерений, соответствующие (7.10), занесите в табл. 7.4, в которую также необходимо перенести значение U при f = f0 из
табл. 7.3.
Таблица 7.4
Измеряют |
|
Вычисляют |
|||
f, кГц |
U, В |
|
Z ( jω) |
|
, Ом |
|
|
||||
Рекомендуется, определив дополнительно две частоты, при которых U = 0,707U0 , вычислить добротность контура, используя (7.11).
7.3.2. Исследование резонанса токов и АЧХ контура с большими потерями
Соберите схему, изображенную на рис. 7.9.
66
|
|
C1 |
i(t) |
R2 |
L1 |
Рис. 7.9
Потери в цепи определяются проводимостью G =1
R2 . Методика
исследования такая же, как в 7.3.1. Результаты измерений занесите в таблицы, аналогичные табл. 7.3 и 7.4. Поскольку АЧХ цепи является более плавной, рекомендуется в диапазонах 8…12 кГц и 16…20 кГц изменять частоту через 2 кГц. По результатам измерений в табл. 7.3 вычислите лишь
G , R =1
G и Q .
7.3.3. Исследование влияния изменения емкости на характеристики контура
Соберите схему, изображенную на рис. 7.10.
C1 C2
i(t) |
R2 |
L1 |
Рис. 7.10
Проведите измерения, аналогичные 7.3.2. Результаты измерений занесите в таблицы, аналогичные табл. 7.3 и 7.4. Поскольку АЧХ цепи является более плавной, рекомендуется в диапазоне 1…4 кГц изменять частоту через 1 кГц, в диапазоне 4…10 кГц через 0,5 кГц, а в диапазоне 10…18 кГц через 2 кГц.
7.4.Требования к отчету
Вотчете должны быть отражены цель работы, все пункты экспериментального исследования и заключение с краткими выводами. По каждому пункту в отчет следует включить его название, схемы исследуемых цепей, таблицы измерений и вычислений, а также необходимые расчеты.
67
Рекомендуется на одном графике построить все АЧХ по 7.2.1 – 7.2.3 и графически рассчитать добротности, на другом – аналогично по 7.3.1 – 7.3.3. Необходимо также письменно ответить на следующие вопросы:
1. Как, используя эквивалентные схемы цепи для ω= 0, ω= ∞ и ω= ω0 ,
определить значения АЧХ на этих частотах и проконтролировать результаты эксперимента? Приведите схемы замещения для этих частот.
2.В чем сходство и в чем различие данных, измеренных и рассчитанных
в7.2.1 и 7.2.2?
3. |
В чем сходство и в чем различие данных 7.2 |
.2 и |
7.2.3? Почему |
диапазон изменения частоты иной? |
|
|
|
4. |
Как, используя эквивалентные схемы цепи для ω= 0, |
ω= ∞ и ω= ω0 , |
|
определить значения АЧХ на этих частотах и проконтролировать результаты эксперимента?
5.В чем сходство и в чем различие данных, измеренных и рассчитанных
в7.3.1 и 7.3.2?
6. В чем сходство и в чем различие данных 7. |
3.1 и 7. 3.2? Почему |
диапазон изменения частоты иной? |
|
Работа№8 ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
ДВУХПОЛЮСНИКОВ
Цель работы: исследование амплитудно-частотных и фазовых характеристик входных сопротивлений LC - и RLC -двухполюсников.
8.1.Подготовка к работе
Вработе необходимо исследовать частотные характеристики реактивного LC -двухполюсника и RLC -двухполюсника, схемы которых представлены на рис. 8.1.
При действии на цепь источника тока реакцией на входе является напряжение и свойства пассивного двухполюсника (ДП) в установившемся синусоидальном режиме определяются входным сопротивлением
Z(jω)= Z(jω)e jϕ(ω) = r(ω)+ jx(ω).
68
L1 C1 |
i |
L2 |
|
|
i0 |
|
|
|
|
|
|
0 |
C1 |
R |
|
|
|
||
L2 |
|
|
R |
|
|
C3 |
|
0 |
|
|
|
|
|
|
а |
|
Рис. 8.1 |
б |
|
|
|
|
|
|
График Z ( jω) , построенный в функции частоты ω, |
является в данном |
|||
случае АЧХ, график аргумента ϕ(ω) – ФЧХ, а графики r(ω) и x(ω) – соответственно вещественной и мнимой частотными характеристиками двухполюсника. Используют также амплитудно-фазовую характеристику (АФХ), представляющую собой геометрическое место значений Z ( jω), построенное в комплексной плоскости, например по графикам АЧХ и ФЧХ.
При резонансе в |
пассивном |
двухполюснике выполняются |
условия |
Im Z ( jω)= 0 и ImY |
( jω)= 0 , т. |
е. на резонансной частоте |
ω0 в |
установившемся синусоидальном режиме ток и напряжение двухполюсника совпадают по фазе: ϕ(ω0) = 0.
Для LC -двухполюсника входное сопротивление будет мнимой дробно-
рациональной функцией ω вида: |
|
|||||
Z ( jω)= jx(ω)= jk |
ω(ω12н −ω2 )(ω22н −ω2 )... |
(8.1) |
||||
|
. |
|||||
(ω12т −ω2 )(ω22т −ω2 )... |
||||||
Нули jωkн |
и |
полюсы |
jωkт сопротивления Z ( jω), определяемые |
|||
соответственно |
из |
условия |
резонанса напряжений Z ( jω)= 0 |
и условия |
||
резонанса токов |
Z ( jω)= ∞, |
совпадают с резонансными частотами LC - |
||||
двухполюсника. Они являются мнимыми числами и располагаются, чередуясь друг с другом, на оси jω плоскости комплексной частоты s = σ+ jω. В зависимости от структуры и элементов цепи в начале координат располагается либо нуль, как в (8.1), либо полюс. Обычно общее число резонансов напряжений и токов на единицу меньше количества реактивных элементов.
69
Используя указанные свойства реактивных двухполюсников, а также свойство dx/dω ≥ 0, можно построить частотные характеристики jx(ω) качественно. Например, для двухполюсника, изображенного на рис. 8.1, а, частотная характеристика jx(ω), приведенная на рис. 8.2, а, может быть построена качественно для ω > 0 исходя из следующих соображений: в цепи возможны лишь 3 резонансные частоты ω1т, ω1н и ω2т; предельные значения сопротивления x(0) = 0 и x(∞) = 0 оцениваются путем анализа эквивалентной схемы замещения при ω = 0 и ω → ∞.
x(ω) |
|Z| |
|
0 |
ω1т ω1н ω2т |
ω |
0 |
ω |
а |
б |
Рис. 8.2
Амплитудно-частотная характеристика этого идеализированного LC- двухполюсника определяется модулем функции, изображенной на рис. 8.2, б, поскольку Z(jω) = jx(ω) = x(ω). АЧХ двухполюсника с реальными
катушками индуктивности и конденсаторами, полученная опытным путем, не принимает нулевых и бесконечно больших значений; она является непрерывной функцией частоты, но при высокой добротности контуров, исследуемых в работе (Q ≥ 15…20), сохраняет большую крутизну в области резонансных значений частоты.
Для RLC -двухполюсника в зависимости от соотношения значений параметров R , L , C резонанс может и не наблюдаться. Следует также отметить, что в RLC -двухполюсниках частоты, соответствующие максимальным и минимальным значениям Z ( jω), в общем случае не
совпадают с резонансными.
Перед экспериментальным исследованием выполните следующее расчетное задание, необходимое для контроля опытных данных:
1. Вычислите резонансные частоты LC -двухполюсника, изображенного на рис. 8.1, а (по указанию преподавателя для 8.2 принять L1 = 25 10−3 Гн,
70