
лабы / 9_Multisim_Езеров / Multisim_метода
.pdf
XFG3 |
XMM6 |
XMM5 |
Key = 1 |
|
|
Key = 2 |
J3 |
X3 |
X4 |
J4 |
|
|
IO1 |
IO5 |
IO3 |
IO7 |
|
|
|
IO2 |
IO6 |
IO4 |
IO8 |
|
|
|
XMM7 |
|
4xp2 |
XMM8 |
J5 |
R |
|
4xp1 |
|
|||||
|
|
|
|
|
Key = 3 |
|
For p.13.2.5
г
Рис. 13.4
13.2.1. Определение z-параметров четырехполюсников
Измерьте указанные в табл. 13.1 напряжения и токи с помощью вольтметров XMM1, XMM2 и амперметров XMM3, XMM4 в цепи, изображенной на рис.13.4, а. Измерения выполните в режиме холостого хода на входе и выходе ЧП1 (X1), сформированного на базе сопротивлений R1 и
R2 (рис. 13.5, а).
1 |
+ |
R |
|
+ |
2 |
1 + |
|
|
+ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
R |
|
|
R4 |
|
|
||||
|
U1 |
|
U2 |
|
|
U1 |
R3 |
U2 |
|
||
|
− |
|
2 |
− |
|
|
− |
|
− |
|
|
1 |
|
|
2′ |
′ |
|
′ |
|||||
|
|
|
|
1 |
|
|
|
|
2 |
||
а б
Рис. 13.5
Аналогичные измерения выполните с помощью вольтметров XMM5, XMM8 и амперметров XMM6, XMM7 для ЧП2 (X2), содержащегося в цепи,
показанной на рис. 13.2, б. ЧП2 построен на базе сопротивлений |
R3 и R4 |
||||||||||||||
(рис. 13.5, б). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты измерений сведите в табл. 13.1. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 13.1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Режим |
|
|
Наблюдают |
|
|
|
|
Вычисляют |
|
|
|
||||
ХХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
U1, В |
I1, мА |
U2 , В |
z11 =U1 I1 , Ом |
z21 =U2 I1 , Ом |
||||||||||
выходе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЧП1 |
ЧП2 |
ЧП1 |
ЧП2 |
ЧП1 |
ЧП2 |
ЧП1 |
ЧП2 |
ЧП1 |
|
|
ЧП2 |
||||
ЧП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
U1, В |
I2 , |
мА |
U2 , В |
z12 =U1 I2 , Ом |
z22 =U2 I2 , Ом |
|||||||||
входе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЧП1 |
ЧП2 |
ЧП1 |
|
ЧП2 |
ЧП1 |
|
ЧП2 |
ЧП1 |
|
ЧП2 |
ЧП1 |
|
|
ЧП2 |
|
ЧП |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
121

Вычислите z -параметры четырехполюсников ЧП1 и ЧП2. Запишите матрицы их z -параметров. Определите параметры элементов эквивалентных Т-образных схем (см. рис. 13.2, а) для обоих четырехполюсников. Убедитесь, что в эквивалентной схеме ЧП1 сопротивление Z3 = 0.
13.2.2. Определение z-параметров последовательно соединенных четырехполюсников
Определите z-параметры последовательного соединения ЧП1 и ЧП2 по методике, описанной в 13.2.1. Для этого измерьте необходимые напряжения и токи с помощью вольтметров XMM2, XMM4 и амперметров XMM1, XMM3 в цепи, изображенной на рис. 13.4, в.
Результаты измерений и расчетов занесите в таблицу, аналогичную табл. 13.1.
Сравните параметры сложного четырехполюсника с соответствующими z-параметрами четырехполюсников ЧП1 и ЧП2.
13.2.3. Определение a-параметров четырехполюсников
Для определения a-параметров ЧП1 и ЧП2 используют режимы ХХ и КЗ на выходах цепей, изображенных на рис. 13.4, а, б соответственно. Измерьте напряжения и токи, указанные в табл. 13.2. Данные для заполнения первой строки табл. 13.2 можно взять из 13.2.1 (первая строка табл. 13.1). Вычислите a-параметры ЧП1, а затем ЧП2; запишите их в матричной форме.
Таблица 13.2
Режим |
|
|
|
Наблюдают |
|
|
|
Вычисляют |
|
|||
ХХ на |
|
U1, В |
I1, мА |
|
|
U2 , В |
a11 =U1 U2 |
a21 = I1 U2 |
||||
выходе |
ЧП1 |
|
ЧП2 |
ЧП1 |
ЧП2 |
|
ЧП1 |
ЧП2 |
ЧП1 |
ЧП2 |
ЧП1 |
ЧП2 |
|
|
|
||||||||||
КЗ на |
|
U1, В |
I1, мА |
|
I2′ , мА |
a12 =U1 I2′ |
a22 = I1 I2′ |
|||||
выходе |
ЧП1 |
|
ЧП2 |
ЧП1 |
ЧП2 |
|
ЧП1 |
ЧП2 |
ЧП1 ЧП2 ЧП1 ЧП2 |
|||
Используя |
z-параметры |
четырехполюсника |
ЧП1, |
найдите |
его |
|||||||
a-параметры также и по формуле (13.2). Сравните их с данными |
||||||||||||
эксперимента. |
|
|
|
|
|
|
|
|
|
|
||
13.2.4. Определение a-параметров каскадно соединенных |
||||||||||||
четырехполюсников |
|
|
|
|
|
|
|
|
|
|||
Определите а-параметры каскадного соединения (см. рис. 13.3, в) |
||||||||||||
четырехполюсников ЧП1 и ЧП2 по методике, |
описанной в 13.2.3, измеряя |
|||||||||||
|
|
|
|
|
|
|
122 |
|
|
|
|
|

напряжения (вольтметрами XMM7, XMM8) и токи (амперметрами XMM5, XMM6) в цепи, показанной на рис. 13.4, г.
13.2.5. Определение передаточных функций и входного сопротивления согласованно-нагруженного симметричного четырехполюсника
Исследуйте режим согласованной нагрузки симметричного четырехполюсника ЧП, составленного из каскадно соединенных четырехполюсников ЧП1 и ЧП2. Определите предварительно по формулам (13.5) и (13.6) характеристическое сопротивление и передаточные функции по напряжению и току. Используйте измерительную схему (рис. 13.4, г) каскадно соединенных четырехполюсников ЧП1 и ЧП2 с подключенным с помощью ключа J4 сопротивлением нагрузки Zн = Zс. На входе и выходе
результирующего четырехполюсника измерьте токи и напряжения. Результаты измерений занесите в табл. 13.3.
Таблица 13.3
Наблюдают |
|
|
Вычисляют |
|
|
|
||
U1, В I1, U2 , |
I2′ , |
Zвх = U1 , Ом Zн = |
U2 |
, Ом |
Hвх = U2 |
HI = |
I2′ |
|
I2′ |
|
|||||||
|
|
I1 |
|
|||||
мА В |
мА |
I1 |
|
U1 |
|
|
||
По данным измерений найдите входное сопротивление четырехполюсника, его сопротивление нагрузки, а также значения передаточных функций по напряжению и току. Сравните полученные данные со значениями характеристического сопротивления и передаточных функций, рассчитанными по формулам (13.5) и (13.6).
13.3. Требования к отчету
Отчет должен содержать цель работы, все пункты исследования и заключение. По каждому пункту необходимо привести его название, схемы исследуемых цепей, таблицы наблюдений и вычислений, требуемые расчеты. Заключение должно содержать краткие выводы, подтверждающие, что цель работы достигнута и результаты ее поняты. Также необходимо письменно ответить на следующие вопросы:
1.Выполняются ли условия обратимости (13.3) и симметрии (13.4) для четырехполюсника ЧП1 в 13.2.1?
2.Чем различаются z-параметры ЧП1 и ЧП2 в 13.2.1?
123
3.Выполняются ли условия обратимости и симметрии для сложного четырехполюсника в 13.2.2?
4.Почему, исходя из схем четырехполюсников ЧП1 и ЧП2, показанных на рис. 13.5, а и б, следует, что их последовательное соединение является регулярным, а сложный четырехполюсник (рис. 13.3, а), составленный из них, симметричен?
5.Выполняются ли условия обратимости (13.3) и симметрии (13.4) для вычисленных a-параметров обоих четырехполюсников в 13.2.3?
6.Выполняются ли условия обратимости и симметрии для результирующего четырехполюсника в 13.2.4?
7.Выполняется ли соотношение (13.9)?
8.Выполняется ли для результирующего четырехполюсника в 13.2.5 условие согласованной нагрузки Zвх = Zн = Zс?
9.Выполняется ли с достаточной точностью равенство HU = HI при согласованной нагрузке?
10. Что больше: z |
или |
1 |
и почему? |
|
|||
11 |
y11 |
|
|
|
|
|
|
Работа № 14 ИССЛЕДОВАНИЕ РЕАКТИВНЫХ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ
Цель работы: ознакомление с простыми реактивными фильтрами верхних и нижних частот и их фильтрующими свойствами.
14.1. Подготовка к работе
Электрический фильтр – это четырехполюсник, который пропускает частотные составляющие сигнала, лежащие в некотором диапазоне частот, называемом полосой пропускания, и задерживает составляющие, лежащие вне этого диапазона, – в полосе задержки.
В работе исследуются фильтры Баттерворта, верхних частот, нижних частот и полосно-пропускающие фильтры (ППФ) с полосой пропускания соответственно fс < f < ∞, 0 ≤ f < fс и fс1 < f < fс2. Граничные частоты fс, fс1, fс2 между полосой пропускания и полосой задержки называют
частотами среза. Фильтры Баттерворта имеют АЧХ, максимально плоскую в
124

полосе пропускания и монотонно убывающую в полосе задержки. Эти фильтры относятся к классу полиномиальных фильтров.
Классическим фильтром называют четырехполюсник, у которого в полосе пропускания затухание α = 0, а в полосе задержки α ≠ 0 .
Функция передачи простого полиномиального реактивного ФНЧ третьего порядка с тремя нулями в бесконечности имеет вид
H (s)= |
|
|
|
|
|
a0 |
|
|
. |
|
|
|
|
|
(14.1) |
|||||
b s3 |
+b s2 |
+b s +1 |
|
|
|
|
|
|||||||||||||
3 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
Коэффициенты (14.1) определяют из условия приближения амплитудно- |
||||||||||||||||||||
частотной характеристикой |
|
H ( jω) |
|
|
к |
заданной в |
|
виде прямоугольника |
||||||||||||
|
|
|
||||||||||||||||||
идеальной характеристики ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
H0( jω) |
|
k, |
0 ≤ |
|
ω |
|
< ωс |
; |
(14.2) |
||||||||||
|
|
|
|
|||||||||||||||||
|
|
|||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0, |
ωс < |
ω |
. |
|
|||||||||
Характеристика H0( jω) изображена на рис. 14.1, б тонкой штриховой
линией.
Рассмотрим приближение с помощью простейшего метода рядов Тейлора (фильтры Баттерворта). Квадрат АЧХ функции передачи (14.1)
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
H ( jω) |
|
= |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
= |
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
4 |
2 6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1+ (b1 − 2b2)ω + (b2 |
− 2b1b3)ω +b3 |
ω |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
0 |
|
|
|
. |
|
|
|
|
(14.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
6 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ B1ω + B2ω + B3ω |
|
|
|
|
|
|||||||
|
Делением числителя на знаменатель получаем разложение в степенной |
|||||||||||||||||||||||||
ряд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H ( jω) |
|
2 |
|
|
2 |
|
|
2 |
2 |
4 |
− |
|
|
|
2 |
|
|
|
6 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
= a0 |
|
{1− B1ω |
+ (B1 |
− B2)ω |
B1(B1 − 2B2) + B3 |
ω + |
...}. (14.4) |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
С другой |
|
стороны, |
производные |
при |
ω= 0 |
идеальной |
плоской |
||||||||||||||||||
характеристики |
|
H0( jω) |
|
|
равны нулю. |
Поэтому все коэффициенты ее ряда |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||
обращаются в нуль, кроме коэффициента при частоте в нулевой степени: H0(0) = k . Приравняв коэффициенты при ω2 и ω4 в (14.4) к нулю, получаем B1 = 0, B2 = 0 , а из равенства H (0) = H0(0) имеем a0 = k . Если нормировать частоту так, чтобы B3 =1, выражение для АЧХ (14.3) ФНЧ Баттерворта n-го
порядка принимает вид: H ( jω *) = k / 
 1+ω *2n .
1+ω *2n .
125

При изменении частоты от нуля до бесконечности АЧХ монотонно спадает от максимального значения k до нуля (рис. 14.1, б). При
нормированной частоте среза ω *с =1 значение H ( jω *с) = k

 2 .
2 .
С повышением порядка n фильтра крутизна спада АЧХ в полосе задержки возрастает.
Определив, как указано ранее, коэффициенты B1, B2 , B3 в (14.4), находим b3 =1, b1 =b2 = 2 ; следовательно, функция передачи фильтра
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H (s) |
|
|
|
a0 |
|
|
|
(14.5) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s3 + 2s2 |
+ 2s +1 |
|
|
|
|||||||||||||||
|
R1 |
|
|
L1 |
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+ |
|
|H (jω)| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U2 |
|
|
k/√¯2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U1 |
|
|
C |
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
ПП |
|
|
|
|
|
n = 3 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
ω |
||||||||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 14.1
Функцию передачи (14.5) необходимо реализовать, т. е. найти схему приемлемой структуры и значения ее элементов.
На рис. 14.1, а изображена одна из таких схем в виде реактивного Т-образного трехполюсника, нагруженного на входе и выходе на нормированные сопротивления R1* = R2* =1. Функция передачи такой цепи,
называемой ФНЧ-прототипом, имеет вид
H(s) =0,5 |
|
0,5s |
3 |
L |
L C |
+0,5s |
2 |
(L |
+ L |
)C |
+0,5s(L |
+ L |
+C |
|
|
|
|
) +1 . (14.6) |
|||||||||||
|
|
|
1* |
2* * |
|
|
1* |
2* |
* |
1* |
2* |
* |
|
|
Приравняв коэффициенты (14.5) и (14.6), имеем 3 уравнения для трех |
||||||||||||||
нормированных параметров: |
|
|
|
|
|
|
|
|
|
|||||
L1*L2*C* = 2; (L1* + L2*)C* = 4; L1* + L2* +C* = 4 , |
|
|||||||||||||
которые дают L1* = L2* =1; |
C* = 2 . Относительный |
уровень |
выходного |
|||||||||||
напряжения k = 0,5. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученные значения параметров относятся к нормированным с частотой среза ωс* =1 и сопротивлениями R1* = R2* =1. Пересчет
параметров по заданным сопротивлениям R1 и R2 , а также частоте среза fс
126

производят, |
как |
|
обычно, |
|
по |
|
|
выражениям |
|
|
L1 = L2 = L1*R2 (2πfс) ; |
|||||||||||||||||||
C = C* (R2 2πfс) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Параметры ФВЧ получают по требуемой частоте среза Ωс, применив |
||||||||||||||||||||||||||||||
частотное преобразование данных ФНЧ с помощью функции |
s = ω02 / p , |
|||||||||||||||||||||||||||||
где p = jω |
– |
|
|
комплексная |
|
|
частота, |
используемая |
для |
вычисления |
||||||||||||||||||||
параметров элементов схемы ФВЧ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Из условия пересчета частот среза ωс и Ωс находят коэффициент |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ω02 = ωсΩc , |
|
|
|
|
|
|
|
(14.7) |
|||||||||||
а затем с учетом (14.7) определяют параметры |
|
|
′ |
|
′ |
′ |
схемы ФВЧ |
|||||||||||||||||||||||
C1 |
= C2 |
и L |
||||||||||||||||||||||||||||
(рис. 14.2, а) по известным параметрам |
L1 = L2 |
и C схемы ФНЧ: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
′ |
′ |
2 |
|
|
|
|
−1 |
, |
′ |
2 |
|
|
|
−1 |
. |
|
(14.8) |
|||||||
|
|
|
|
|
|
C1 |
=C2 |
= (ω0L1) |
|
L |
=(ω0C) |
|
|
|
||||||||||||||||
|
R1 |
C1′ |
|
|
C2′ |
|
|
|
|
|
|
|
|
|
|
|H(jω)| |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
ПП |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U1 |
L |
′ |
|
|
|
|
|
R2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
– |
|
|
|
|
|
|
|
|
U2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Ωc |
|
ω |
||
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
Рис. 14.2
Таким образом, по формулам (14.7) и (14.8), зная параметры фильтрапрототипа L1 = L2 , С и частоту среза Ωс, рассчитывают параметры
фильтра верхних частот.
Аналогично можно определить и другие характеристики ФВЧ по данным ФНЧ-прототипа. На рис. 14.2, б показана амплитудно-частотная характеристика схемы фильтра верхних частот.
Параметры ППФ получают по заданным частотам среза Ωс1 и Ωс2, применив частотное преобразование параметров ФНЧ с помощью функции
s = ( p2 + ω2) / (ap), |
(14.9) |
0 |
|
где ω02 = Ωс1Ωс2 , a = (Ωс2 − Ωс1) / ωс .
127

Следовательно, характерная частота ФНЧ s = 0 преобразуется согласно
формуле (14.9) к частоте ППФ |
|
p = ± jω0 = ± j |
Ωс1Ωс2 |
и находится |
|||
между частотами Ωс1 |
и Ωс2. Амплитудно-частотная характеристика ППФ |
||||||
показана на рис. 14.3, б. Схема ППФ изображена на рис. 14.3, а. |
|||||||
В случае a =1 |
значения |
параметров продольных ветвей схемы, |
|||||
выполненных в виде последовательных L1C1-, |
L2C2 -контуров: |
||||||
|
|
|
|
′ ′ |
′ |
′ |
|
′ |
′ |
; |
′ |
′ |
|
2 |
|
L1 = L2 = L1 |
C1 |
= C2 |
=1 (ω0L1), |
||||
|
|
|
|
|
|
′′ ′′ |
|
и поперечной ветви, выполненной в виде параллельного L3C3 -контура, |
|||||||
|
′′ |
|
′′ |
|
2 |
|
|
|
C3 = С, |
L3 |
=1 (ω0C ), |
||||
где L1, C – параметры элементов схемы ФНЧ-прототипа.
R1 |
C′ |
′ |
|
L′ |
C′ |
|
|
|H(jω)| |
|
|
|
|
1 |
L1 |
|
2 |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
′′ |
′′ |
|
|
U |
2 |
k |
|
|
|
|
|
|
R2 |
2 |
|
|
|
|
|||||
U1 |
|
C3 |
L3 |
|
|
ПП |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ω |
c1 |
ω |
c2 |
ω |
|
а |
|
|
|
|
|
|
б |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 14.3
Для АЧХ фильтров обычно применяют логарифмический масштаб и вводят понятие затухания (коэффициент затухания), измеряемого в децибелах:
|
|
|
α(ω) = 20lg(1/ |
|
H (ω) |
|
) = 20lg(U1 / U2). |
|
(14.10) |
||||||||||||
|
|
|
|
||||||||||||||||||
Затухание сигнала на выходе фильтра α = 0 при U2 =U1, |
α = 3 дБ |
||||||||||||||||||||
при U2 =U1 / |
|
|
, α = 6 дБ при U2 =U1 / 2 и т. д. |
|
|
|
|||||||||||||||
2 |
|
|
|
||||||||||||||||||
α(ω), |
|
|
|
|
α(ω), |
|
|
|
|
α(ω), |
|
|
|
||||||||
дБ |
|
|
|
|
дБ |
|
|
|
|
дБ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||
0 |
|
|
|
ω |
|
0 |
|
|
|
|
ω |
|
|
0 |
|
|
|
|
|||
|
|
ωс |
ωс |
|
|
|
|
|
|
||||||||||||
|
|
|
|
ωс1 |
ωс2 |
ω |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а б в
Рис. 14.4
128
На рис. 14.4, а–в показаны для случая k =1 характеристики затухания ФНЧ, ФВЧ и ППФ соответственно.
14.2. Исследования с применением моделирующих компьютерных программных средств Multisim
Для начала работы необходимо включить компьютер и на рабочем столе открыть папку Лаб. раб. ТОЭ и в ней Лаб. раб. № 14. Схема для исследований представлена на рис. 14.5.
Схемы LC -фильтров нижних и верхних частот собираются из элементов с помощью ключей S1–S6, управляемых клавишами Key1 – Key6.
14.2.1. Определение частотных характеристик фильтра нижних частот
Для исследования LC-фильтра нижних частот активируйте схему, показанную на рис. 14.5.
Соберите фильтр нижних частот по схеме на рис. 14.1 ( R1 = R2 = 980 Ом, L1 = L2 = 24 мГн, C3 = 0,05 мкФ).
129
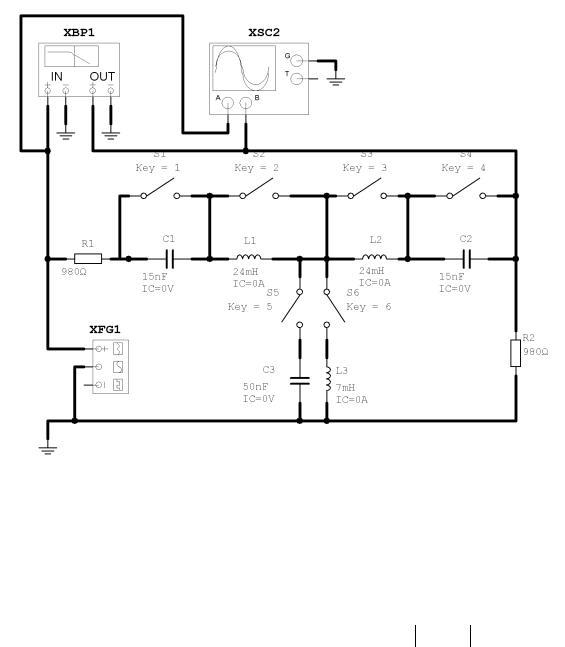
Рис. 14.5
Откройте лицевую панель генератора XFG1 и установите амплитуду синусоидальных сигналов Um =1 В и частоту f =1 кГц. Cнимите АЧХ
фильтра нижних частот с помощью анализатора частотных характеристик (Bode Plotter XBP1), установив в режиме Lin, Magnitude частотный диапазон
(I = 1, F = 20), диапазон значений (I = 0, F = 0.51).
Снимите амплитудно-частотную характеристику H ( jω) =Uвых / Uвх
для 7–8 точек с помощью измерительного курсора (внизу экрана). Определите полосу пропускания фильтра, на которой значение АЧХ
равно 0,707 от ее максимального значения. Результаты измерений занесите в табл. 14.1.
Фазочастотную характеристику φ(ω) снимите в режиме Phase в том же диапазоне частот, установив значения (I = -200Deg, F = 200Deg). Результаты измерений занесите в табл. 14.1. При измерениях зафиксируйте значения ФЧХ на границе полосы пропускания фильтра.
Таблица 14.1
Частота |
Измеряют |
Вычисляют |
|
|
130 |
