
Министерство цифрового развития, связи и массовых коммуникация Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Информатики
Лабораторная работа №1
По дисциплине «Численные методы»
На тему «Методы решений нелинейных уравнений»
Вариант 23
Выполнил: студент группы
Проверил: преподаватель
Москва, 2024
Цель работы:
1. Выбрать индивидуальное задание из табл. 1-1:
• нелинейное уравнение;
• методы решения нелинейного уравнения для выполнения 3-х итераций;
2. Отделить корни заданного уравнения графическим и аналитическим
методом с использованием средств пакета Scilab.
3. Для каждого из заданных методов провести исследование функции
нелинейного уравнения:
• проверить выполнение условий сходимости вычислительного
процесса, в случае расходящегося процесса – сделать необходимые
преобразования для обеспечения сходимости;
• выбрать начальное приближение к корню;
• сформулировать условие окончания этапа уточнения корня.
4. С использованием итерационной формуле 1-го заданного методу провести расчет трех итераций с использованием средств пакета Scilab.
Результаты расчета свести в табл. 1-2.
5. Оценить погрешность результата после 3-х итераций.
6. Для 2-го заданного метода выполнить решение уравнения с точностью 10-4 , создав программу, реализующую заданный метод. Произвести
расчет, а результаты решений свести в табл. 1-2.
Найти решение нелинейного уравнения на отделенном отрезке с использованием функции fsolve пакета Scilab.
Индивидуальное задание
![]()
Выполнение задания
Часть1 - Метод итераций
Отделение корней в MathCad
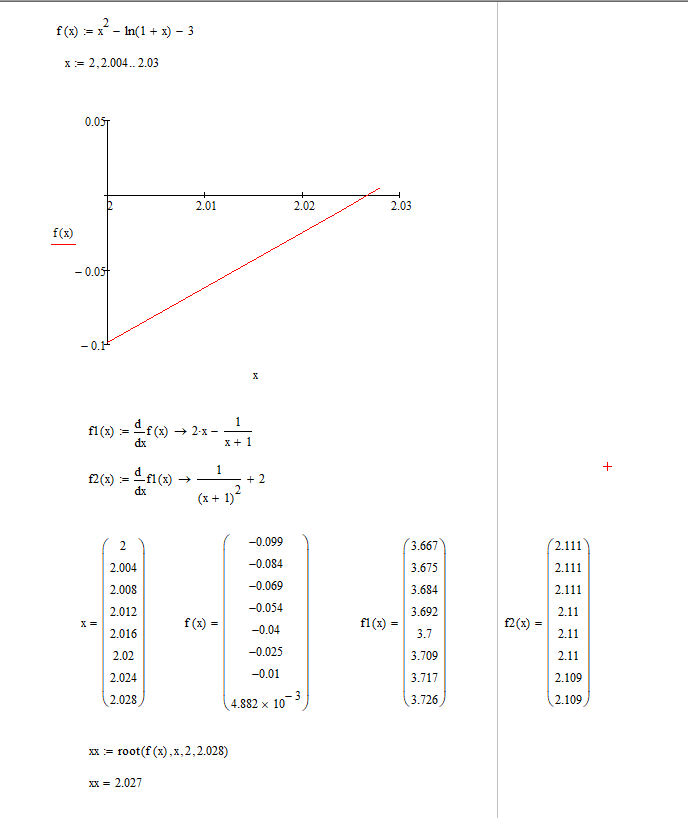
Производим ручной расчет
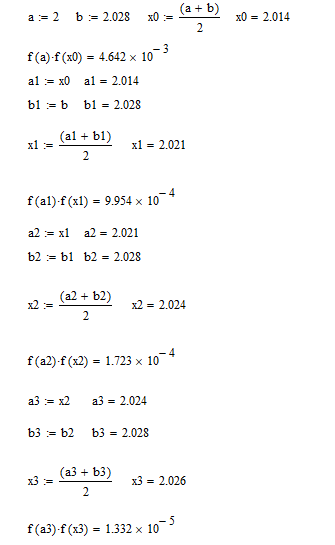
Результаты вычислений:
n |
a |
b |
F(a) |
F(b) |
(a+b)/2 |
F((a+b)/2) |
b-a |
F(a)*f(x) |
0 |
2 |
2.028 |
-0,099 |
4.882*10^-3 |
2.014 |
-0.047 |
0.028 |
4.642*10^-3 |
1 |
2.014 |
2.028 |
-0.047 |
4.882*10^-3 |
2.021 |
-0.021 |
0.014 |
9.954*10^-4 |
2 |
2.021 |
2.028 |
-0.021 |
4.882*10^-3 |
2.024 |
-8.146*10^-3 |
0.007 |
1.723*10^-4 |
3 |
2.024 |
2.028 |
-8.146*10^-3 |
4.882*10^-3 |
2.026 |
-1.635*10^-3 |
0.004 |
1.332*10^-5 |
Погрешность:
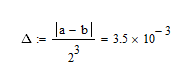
Итоговый корень уравнения:
X=2.026±3.5*10^-3
Часть 2 - Метод Ньютона
Расчет на ПК
import math
def f(x):
return x**2 - math.log(1 + x) - 3
def df(x):
return 2*x - 1/(1+x)
def newton_method(func, deriv, x0, max_iter):
iteration = 0
while iteration < max_iter:
x1 = x0 - func(x0) / deriv(x0)
x0 = x1
iteration += 1
return x1
x0 = 1
max_iterations = 1000
result = newton_method(f, df, x0, max_iterations)
print("x =", ‘%.4f’%result)
![]()
Cхема работы алгоритма
Вывод
В данной работе были изучены и решены уравнения методами половинного деления и Ньютона.
