
Министерство цифрового развития, связи и массовых коммуникация Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Информатики
Лабораторная работа №7
По дисциплине «Численные методы»
На тему «Методы многомерной оптимизации»
Вариант 23
Выполнил: студент группы .
Проверил: преподаватель
Москва, 2024
Цель работы
1. Выбрать индивидуальное задание из табл. 6-1 для решения задачи
оптимизации функции двух переменных:
• Функцию –f(x, y);
• Методы, заданные для ручного расчета и для расчета на компьютере.
2. Проверить условия существования точки минимума заданной функции f(x,y).
3. Решить задачу многомерной оптимизации аналитическим методом.
4. Выбрать начальную точку x0, y0 итерационного процесса оптимизации.
5. Провести расчет 3-х итераций 1-м заданным методом, а результаты расчета свести в табл. 6-2.
6. Написать программу получения координат минимума функции 2м
заданным методом с точностью 10^-4 , результаты расчета свести в табл. 6-3.
7. Используя данные 3-х итераций, построить в одном графическом окне две траектории спуска (НСА и ГДШ).исделать вывод о правильности проведенных расчетов.
8. Решить задачу многомерной оптимизации с использованием функции optim пакета Scilab, сравнить полученные координаты точки минимума, вычисленные с использованием пакета, с координатами, полученными аналитическим методом.
Индивидуальное задание
![]()
Ручной расчет - ГДШ
Расчет на ПК - НСА
Выполнение задания
Часть 1 - ручной рассчет
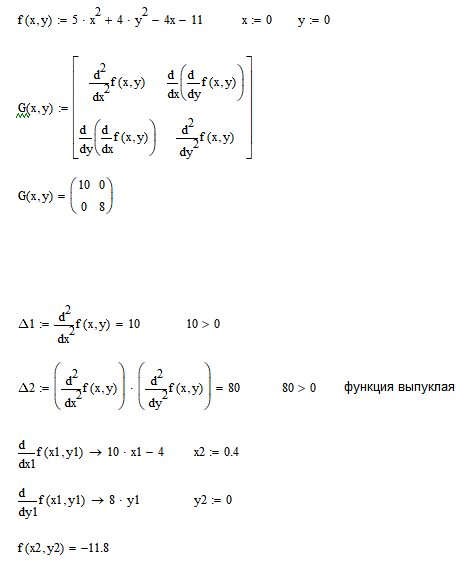
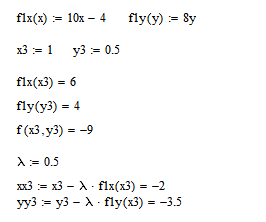

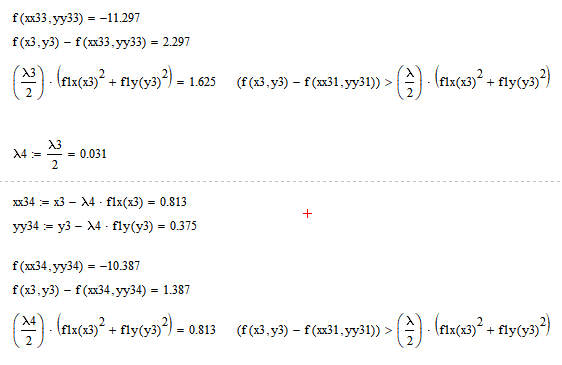
k |
x |
y |
F(x,y) |
F’x |
F’y |
λ |
0 |
1 |
0.5 |
-9 |
6 |
4 |
0.5 |
1 |
-0.5 |
-0.5 |
-6.75 |
-9 |
-4 |
0.25 |
2 |
0.25 |
0 |
-11.688 |
-1.5 |
0 |
0.125 |
3 |
0.625 |
-0.25 |
-11.297 |
2.25 |
2 |
0.063 |
После 3х итераций - xmin=-0.5 ymin=-0.5 f=-11.297
Часть 2 - расчет на ПК
import math
def Lam(x, y):
Lamda = (20 * x**2 - 8 * x + 48 * y**2) / (200 * x**2 - 160 * x + 32 + 384 * y**2)
return Lamda
def f(x, y):
func = 5 * x**2 + 4 * y**2 - 4 * x - 11
return func
def gx(x):
dx = 10 * x - 4
return dx
def gy(y):
dy = 8 * y
return dy
def MO(x, y, eps, max_iter):
k = 1
while k <= max_iter:
L = Lam(x, y)
x -= L * gx(x)
y -= L * gy(y)
print(f"{k}: x = {x}, y = {y}")
k += 1
return x, y
start_x = 1
start_y = 1
eps = 0.0001
max_iter = 10
xmin, ymin = MO(start_x, start_y, eps, max_iter)
print("Минимум для x:", xmin)
print("Минимум для y:", ymin)
Результаты кода

Таблица траекторий спуска

Схема работы алгоритма
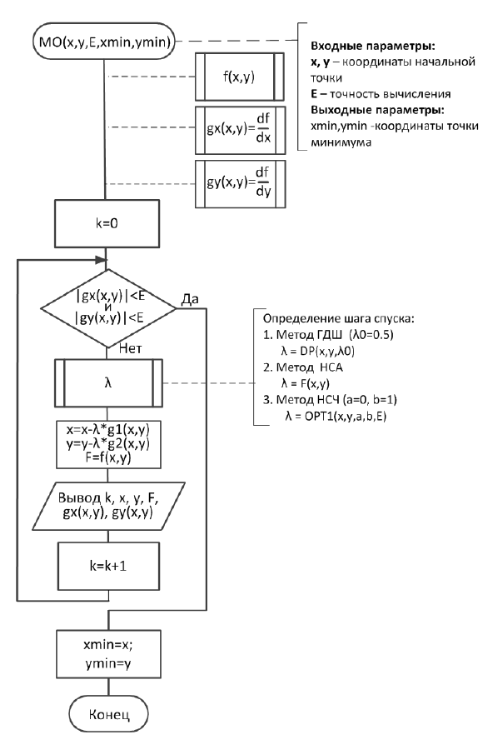
Вывод
В данной работе мною были изучены методы многомерной оптимизации и выполнено задание на ручной расчет и расчет на ПК.
