2Министерство цифрового развития, связи и массовых коммуникация Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Информатики
Лабораторная работа №5
По дисциплине «Численные методы»
На тему «Методы решений обыкновенных дифференциальных уравнений»
Вариант 23
Выполнил: студент группы
Проверил: преподаватель
Москва, 2024
Цель работы
1. Выбрать индивидуальное задание в табл. 4-1 для решения
обыкновенных дифференциальных уравнений:
• дифференциальное
уравнение
• интервал [a; b], где ищется решение дифференциального уравнения;
• начальные условия x0, y0;
• шаг интегрирования h0.
2.
Найти
аналитическое решение
заданного
дифференциального уравнения, полагая
его точным.
3.
Создать
в сценарии функцию для вычисления
значений полученного решения
на
отрезке [a;b] с шагомh0.
4.
Создать
в сценарии функцию для вычисления
значений численного решения
дифференциального уравнения методом
Эйлера
-
в
точках отрезка [a;b] с шагом h0
5.
Вычислить
значения погрешностей
для
6.
Написать
и выполнить программу, реализующую
программу
решения
дифференциального уравнения методом
Рунге-Кутта
4-го
порядка
в
точках отрезка [a;b] с шагом h0, обеспечив
с
использованием
метода автоматического выбора шага,
точность 10^-4
7.
Вычислить
значения погрешностей
для
8.
Найти решение дифференциального
уравнения
с
использованием функции пакета Scilab ode.
9.
Проиллюстрировать
решения
в одной системе
координат.
Индивидуальное задание
x0 = 0 y0 = 1 h0 = 0.2 a = 0 b = 0.6
Выполнение задания
Часть 1 - ручной рассчет
Решим аналитически y’=2xy:
dy/dx=2xy dy/y=2xdx
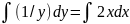
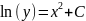
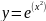
Часть 2 - расчет на ПК
import math
def df(x, y):
f = 2 * x * y
return f
def rung(x, y, h, m):
k1, k2, k3, k4 = 0, 0, 0, 0
for j in range(1, m + 1):
k1 = df(x, y)
k2 = df(x + h / 2, y + h * k1 / 2)
k3 = df(x + h / 2, y + h * k2 / 2)
k4 = df(x + h, y + h * k3)
y = y + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)
x = x + h
return y
def diff(x0, y0, b, h0, eps):
n = math.ceil((b - x0) / h0)
for i in range(1, n + 1):
m = 1
y = rung(x0, y0, h0, m)
while True:
y1 = y
h = h0 / 2
x = x0
y = y0
m = 2 * m
y = rung(x, y, h, m)
if abs(y - y1) / 15 < eps:
break
x0 = x0 + h0
y0 = y
print(f"x = {x0:.1f}, y = {y}")
x0 = 0
y0 = 1
a = 0
b = 0.6
h0 = 0.2
eps = 0.0001
diff(x0, y0, b, h0, eps)
Результаты кода
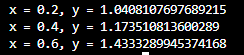
Графики двух методов решения
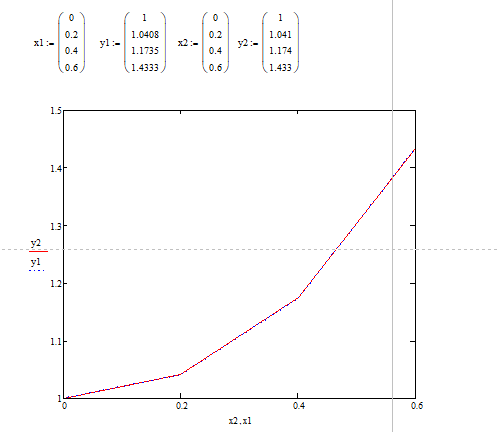
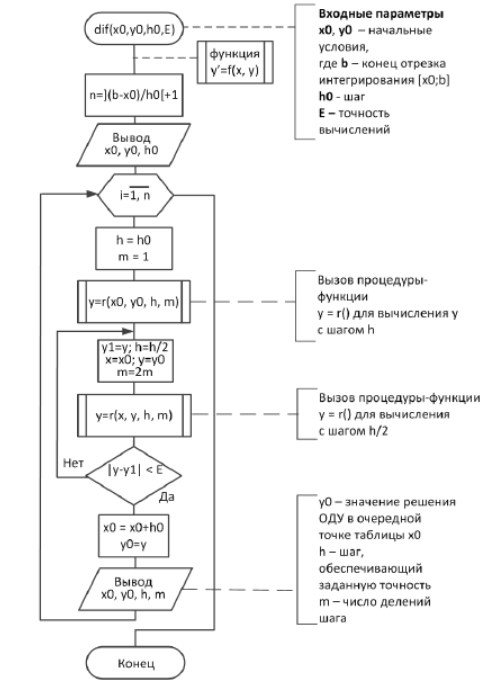
Схема работы алгоритма
Вывод
В данной работе мною были изучена методы решений обыкновенных дифференциальных уравнений.