
Министерство цифрового развития, связи и массовых коммуникация Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Информатики
Лабораторная работа №2
По дисциплине «Численные методы»
На тему «Интерполяция функций»
Вариант 23
Выполнил: студент группы
Проверил: преподаватель
Москва, 2024
Цель работы
1.Выбрать из таблицы 2–1 индивидуальное задание для
интерполяции:
• точку интерполяции x=a для интерполяции многочленом Ньютона;
• точку интерполяции x=b для интерполяции многочленом Лагранжа;
2. Для интерполяции в точке x=a выбрать из таблицы 2–2 с
интерполируемой функцией 4 подходящих узла для построения
многочленов 1, 2 и 3-ей степени.
3. Перенумеровать узлы интерполяции для каждого из методов
интерполяции. Занести перенумерованные узлы в таблицы вида 2–3.
4. Выполнить вручную интерполяцию по заданной формуле в
заданной точке x=a или x=b многочленами 1–й, 2–й и 3–й степени:
• заполнить таблицу конечных разностей (для интерполяционной
формулы Ньютона);
• записать интерполяционные формулы для 1, 2 и 3-ей степени
многочлена;
• выполнить расчеты по интерполяционным формулам для каждой
степени многочлена; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты
округлять до 4 знаков после десятичной точки.
• занести полученные результаты в таблицу вида 2–4;для
многочленов 1–й и 2–й степени вычислить и занести в таблицы 2-4 и 2-5 оценки погрешности интерполяции: модули разности между текущим Pk(x) (Lk(x)) и следующим Pk+1(x) (Lk+1(x)) значением
многочлена.
• 5. Решить задачу интерполяции в точке на компьютере.
Вычислять модули разности между текущим Pk(x) (Lk(x)) и
следующим Pk+1(x) (Lk+1(x)) значением многочлена в т. Х до тех пор, пока эта разность не станет <=0.001.
• Примечание. Для функции, заданной в таблице 2-1, четырех узлов
будет достаточно для решения данной задачи. В общем случае, для
решения задачи интерполяции в точке, может понадобится добавить
большее количество узлов, хотя и это не гарантирует решение.
Индивидуальное задание
![]()
0.23 - Ньютон
0.81 - Лагранж
Выполнение задания
Часть 1 - формула Ньютона, ручной расчет
Находим 4 подходящих узла для построения многочлена

Заполнение таблицы конечных разностей
|
0 |
1 |
2 |
3 |
X0 |
0.2 |
0.25 |
0.3 |
0.35 |
Y0 |
-4.024 |
-3.95 |
-3.861 |
-3.7555 |
dX1 |
0.05 |
0.05 |
0.05 |
0.05 |
dY1 |
0,074 |
0,089 |
0,1055 |
0,1235 |
dY2 |
0.015 |
0,0165 |
0,018 |
|
dY3 |
0,0015 |
0,0015 |
|
|
Производим расчет в Mathcad

Запишем результаты в таблицу
степень |
P(x) |
погрешность |
1 |
-3.98 |
0.001 |
2 |
-3.981 |
0 |
3 |
-3.981 |
|
Часть 2 - формула Лагранжа, расчет на ПК
Находим 4 подходящих узла

Меняем нумерацию узлов
X0 |
0.85 |
X1 |
0.8 |
X2 |
0.9 |
X3 |
0.75 |
Расчет на ПК
def interpolation(xi, x, y):
n = len(x)
result = 0
for i in range(n):
term = y[i]
for j in range(n):
if j != i:
term *= (xi - x[j]) / (x[i] - x[j])
result += term
return result
x = [0.85, 0.8, 0.9, 0.75]
y = [-2.1375, -1.816, -1.463, -1.077]
x0 = 0.83
x01 = 0.85
x02 = 0.8
x03 = 0.9
x04 = 0.75
interpolation_1 = interpolation(x02, x, y)
interpolation_2 = interpolation(x03, x, y)
interpolation_3 = interpolation(x04, x, y)
y01 = (interpolation_1)
y02 = (interpolation_2)
y03 = (interpolation_3)
z1 = abs(y01-y02)
z2 = abs(y02-y03)
print(f"x={x0}")
print(f"y={y01}")
print(f"y={y02}")
print(f"y={y03}")
print(f"погрешность_1 = {z1} погрешность_2 = {z2}")
Результат расчета
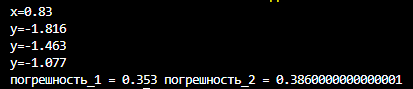
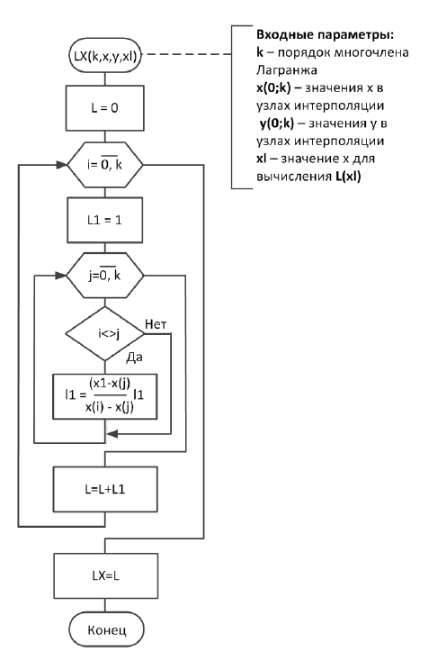
Схема работы алгоритма
Вывод
В данной работе мною были изучена интерполяция функций методами Лагранжа и Ньютона. Были проведены интерполяции каждым методом
