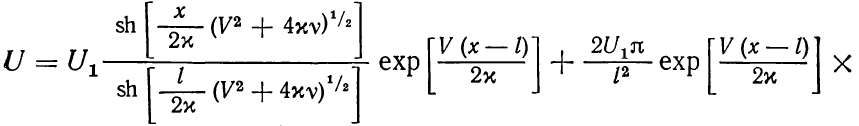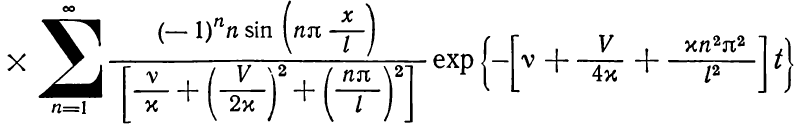теплоперенос
.docxЗона аэрации, глубокие горизонты и нейтральный слой.
Часть литосферы до глубин 200-300 м располагается в зоне, подверженной интенсивному влиянию солнечной радиации, в ней происходит усиленный водообмена зоны аэрации при вовлечении атмосферных и грунтовых вод. Вышеупомянутое и условия передачи тепла (соотношение кондуктивной и конвективной составляющих), а также термические свойства воды и горных пород в зоне гипергенеза являются определяющими для особенностей гидро-геотермического режима, они обуславливают значительное влияние на него климатических (ландшафтно-климатических) особенностей регионов. В случае геотермальных ресурсов глубоких горизонтов (> 0,5 - 1 км), для которых основные теплофизические параметры горных пород, форма переноса тепла и тепловой поток обусловлены с внутренними источниками, ресурсы зоны аэрации (до глубин 0,1 - 0,2 км) находятся под непосредственным воздействием комплекса климатических (ландшафтноклиматических) и гидрологических факторов, с одной стороны, а с другой - геологическим, геотермическим и гидрогеологическим свойствам недр. Тепловой режим зоны аэрации и активного водообмена характеризуется временными изменениями геотемпературного поля, периодическими и других колебаниями прихода энергии Солнца, что совершенно не характерно для глубоких слоев с глубинами залегания от 500 м до 1 км, в случае последних воздействие эндогенных источников можно считать в той или иной степени стационарным. В геотермии решающим является положение "нейтрального слоя", под которым понимается условной расчетной глубины залегания подошвы слоя, на которой влияние многолетних (до 100 лет) климатических циклов колебания температур сводится к нулю. Данный слой является точкой отсчета глубинных температур при геотермических исследованиях. По мнению большинства ученых изменения температуры на более глубоких слоях, чем нейтральный, обусловлено только глубинным теплом Земли. [8]
Концептуальная модель продуктивного геотермального резервуара может быть получена путём анализа данных по распределению температуры, зон притоков горячей воды в скважины, а также структурных и геологических характеристик месторождения. [4]
При конструкции важно учитывать необходимость экологичной утилизации отработанных геотермальных растворов. В качестве эффективного метода предлагается обратная закачка отработанных растворов в породы геотермальные резервуара. [5]
Геотемпературное поле недр было сформировано в процессе эволюции планеты, оно остается нестационарным и является отражением современного теплового баланса Земли - соотношения общих тепловых потерь в космическое пространство ∑Q и интенсивности его внутренних Qв, внешних Qс источников теплоты и аккумуляции его в недрах Qа: ∑Q = Qв + Qс – Qа
Какое место занимают различные источники теплоты в тепловом балансе планеты и какое влияние на тепловой планетный режим планеты, представляется дискуссионным вопросов, окончательный ответ на который еще не дан. По мнению большинства специалистов разогрев Земли продолжается, однако ∑Q = const. Средние температуры земной поверхности изменяются незначительно - около 15 °С. В настоящее время глубина зоны оттока тепла составляет около 1000 км. Согласно оценке Е.А. Любимовой, несмотря на общий разогрев планеты в течение последних 1-2 млрд. лет происходит определённое снижение температуры верхних слоев зоны оттока (около 300 км). Основной внешний источник тепла в уравнении выше - солнечная радиация. Она характеризуется ритмичным характером: в зависимости от длины цикла вызывает колебания температуры, которые затухают на различной глубине. В рамках годового цикла солнечная энергия Qс устанавливает тепловой режим приповерхностной толщи пород, так называемой гелиотермозоны, глубина которой составляет 20-30 м. На данной глубине располагается нейтральный слой пород, характеризующийся практически постоянной температурой Т0. Этот слой - верхняя граница геотермозоны, её тепловой режим определяется конкуренцией генерации тепла Qв, его аккумуляции Qа и условий теплопереноса в недрах. По мнению большинства исследователей основным источником тепла внутри Земли является энергия радиоактивного распада. Принято считать, что на первых порах развития Земли, при равномерном распределении радиоактивных элементов на единицу ее массы, происходил разогрев планеты в основном за счет изотопов с малым периодом полураспада (10Be, 26Al, 36Cl и др.). Спустя 1-2 млрд. лет температура глубинного вещества приняла значения, при которых началось его плавление и гравитационная дифференциация. Таким образом были образованы оболочки Земли и произошла концентрация радиоактивныех элементов в рамках земной коры и верхней мантии. На поздних и современном стадиях развития важную роль в изменении теплового баланса Земли могут играть только долгоживущие изотопы 238U, 232Th, 60K и т.д.
Большое значение для формирования теплового баланса Земли возможно имели экзотермические реакции. Например, лишь при образовании воды выделилось тепло, которое можно сравнить с его суммарной генерацией долгоживущими изотопами. Также значимыми источниками внутриземного тепла являются тектонические, метаморфические и магматические процессы. Данные факты означают, что интенсивность любого из основных источников тепловой энергии является обеспечением ее современных потерь ∑Q и возможности накопления в недрах Qа. Так как эти источники сопоставимы в энергетическом отношении, то следует отметить важность дальнейшего исследования их взаимодействия и возможность очень неравномерного распределения генерации тепла, определяющей особенности теплового режима различных участков недр. Процессы теплопереноса в недрах Земли происходят в результате совместного действия теплопроводности, конвекции и теплового излучения. Так как в общем случае теплопроводность является основным видом передачи тепла в земной коре, то происходит постоянный рост температуры с увеличением глубины. Плотность глубинного теплового потока qr, коэффициент теплопроводности пород λ, и геотермическим градиентом G связаны между собой, эта связь определяется законом Фурье:
qr G .
Данные большого ряда измерений свидетельствуют о том, что средняя плотность глубинного теплового потока на суше и в океане составляет 0,043 ккал/(м2 .ч). На глубине величина геотермического градиента заметно уменьшается, так как происходит рост теплопроводности горных пород с увеличением их плотности. Для примерных оценок среднее значение G верхнего слоя земной коры следует считать равным 0,02 °С/м, нижнего слоя - 0,015 °С/м, верхней мантии - 0,009 °С/м. Для первых километров осадочного чехла G ≈ 0,03 °С/м. Значительную роль в создания теплового режима недр играет конвективный теплоперенос, который возникает при нагревании и тепловом расширении жидкостей в поле тяготения. При фильтрации же подземных вод в осадочных и трещиноватых кристаллических породах важна конвекция, особенно в случае верхних водонасыщенных слоёв земной коры, а также зонах активного вулканизма.
Для нормального геотемпературного поля первых километров земной коры характерен в большей степени быстрый рост температуры пород Т с глубиной. Если G и λ постоянны, оно определяется согласно уравнению
![]() ,
где То
и Но
соответственно температура и глубина
пород нейтрального слоя. [8]
,
где То
и Но
соответственно температура и глубина
пород нейтрального слоя. [8]
Прежде чем перейти к рассмотрению математического аппарата, применяемого в данной сфере, приведём некоторые важные уточнения.
Под теплопереносом в последующем понимается процесс переноса тепла из недр Земли к поверхности, который происходит по разным механизмам, соответственно выделяется четыре основных типа теплопереноса: кондуктивный, конвективный, лучистый и экситонный. Кондуктивная теплопередача – процесс переноса кинетической энергии от одних молекул к другим, происходящий при столкновениях, имеет место осуществляется там, при наличии пространственного градиента температуры. В случае конвективного теплопереноса перенос тепла происходит в результате перемещения макрочастиц среды. Глубинная конвекция в глобальном масштабе имеет место в мантии и внешнем ядре Земли. В районах, близких к поверхности Земли она связана с наличием воды и происходит как гидротермальная циркуляция, это приводит к перераспределению температур и кондуктивного теплового потока в континентальной коре и части верхней мантии под ней. [12]
Теплопроводность, или точнее коэффициент теплопроводности λ, Вт/м · К, - это коэффициент пропорциональности закона Фурье, который связывает плотность теплового потока q, Вт/м2 , с градиентом температур grad T, К/м:
q = −λ grad T.
Влажность и пористость оказывают влияние на теплопроводность горных пород. Сухие и пористые породы характеризуются меньшим коэффициентом теплопроводности, чем монолитные и влажные. При наличие в порах пород движущейся жидкости можно говорить об изменении механизма теплопереноса, кроме кондуктивного происходит конвективный теплоперенос. Тепловое сопротивление ε, м · К/Вт, — величина, обратная теплопроводности: ε = 1/ λ.
Удельная теплоемкость вещества C, кДж/кг · К, определяется формулой
C = dQ/ mdT ,
где dQ, кДж, — количество тепла, подведенное к массе вещества m, кг, для нагрева ее на dT, К. Коэффициент температуропроводности a, м2/с, является характеристикой скорости изменения температуры единицы объема среды в нестационарных процессах и рассчитывается по формуле
a = λ/ Cρ,
где ρ — плотность породы, кг/м3 . [13]
Начало разработки и соответствующих работ невозможно без предварительной оценки теплового потенциала перспективного геотермального месторождения. Эта оценка является важнейшей задачей, которая определяет обоснованность и целесообразность разработки месторождения. Чтобы решить данную задачу, необходимо использовать различные математические модели, с помощью которых можно описать физические процессы высокой сложности, имеющие место в недрах Земли.
Общие потенциальные геотермальные ресурсы (валовый потенциал) в стационарном случае следует оценивать с учётом следующего допущения: массив при добыче тепловой энергии может быть охлажден до температуры окружающей среды. Теоретически это допустимо, однако на практике это представляется маловероятным. Расчетная формула записывается следующим образом:
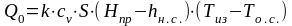 ,
,
где
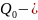 получаемое
тепло;
получаемое
тепло;
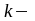 коэффициент
перехода от тепловой энергии к условному
топливу;
коэффициент
перехода от тепловой энергии к условному
топливу;
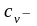 объемная
теплоемкость породы, усредненная по
разрезу, ккал/(м
объемная
теплоемкость породы, усредненная по
разрезу, ккал/(м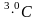 );
);
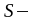 площадь
участка, района, региона,
площадь
участка, района, региона,
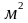 ;
;
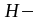 прогнозируемая
глубина бурения, м;
прогнозируемая
глубина бурения, м;
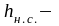 глубина
нейтрального слоя, м;
глубина
нейтрального слоя, м;
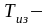 средняя
температура массива в границах намеченной
глубины бурения (средняя изотерма):
средняя
температура массива в границах намеченной
глубины бурения (средняя изотерма):
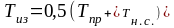 ,
,
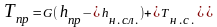 ;
;
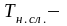 температура
нейтрального слоя,
температура
нейтрального слоя,
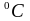 ;
;
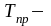 температура
пород на прогнозируемой глубине бурения,
температура
пород на прогнозируемой глубине бурения,
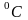 ;
;
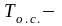 температура
окружающей среды,
;
температура
окружающей среды,
;
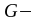 усредненный
по разрезу геотермический градиент.
усредненный
по разрезу геотермический градиент.
Для того, чтобы учесть изменения по времени, следует прибегнуть к использованию дифференциальных уравнений.
Проекция суммарного теплового потока на вертикальную ось с учетом двух механизмов распространения тепла – кондуктивный перенос и конвективный перенос, можно выразить формулой
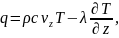
где
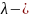 коэффициент
теплопроводности водонасыщенной породы,
c
коэффициент
теплопроводности водонасыщенной породы,
c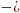 теплоемкость воды,
теплоемкость воды,
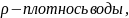
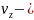 проекция скорости на вертикальную ось.
проекция скорости на вертикальную ось.
В случае учета только конвекции при установившемся режиме уравнение теплопроводности имеет вид обыкновенного
дифференциального уравнения
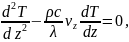
Его аналитическое решение является стандартной задачей и приводит к определению объемов выноса тепла.
В общем случае теплоперенос в водонапорных системах описывается
уравнением
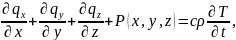
где
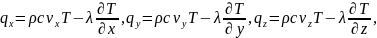
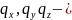 проекции
теплового потока на координатные оси,
проекции
теплового потока на координатные оси,
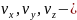 проекции
скорости фильтрации на координатные
оси,
проекции
скорости фильтрации на координатные
оси,
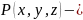 интенсивность
источников тепла.
интенсивность
источников тепла.
Скорость фильтрации определяется из уравнения фильтрации флюида
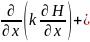
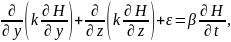
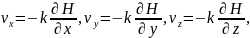
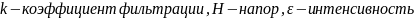
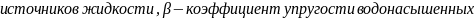
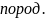 [8],
[2], [15].
[8],
[2], [15].
Математические схемы расчёта теплопереноса в недрах.
Процесс распространения тепла в пористой среде, которая насыщена жидкостью, можно описать уравнением теплопроводности:
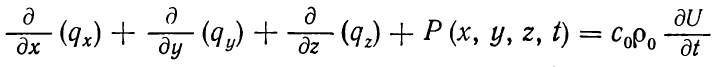 (1.1)
(1.1)
,где
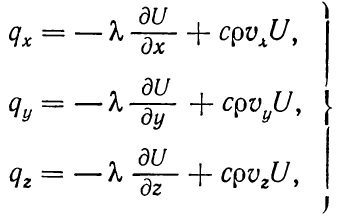 (1.2)
(1.2)
В формулах выше приняты следующие обозначения: qx, qy, qz — проекции теплового потока на оси координат; λ — коэффициент теплопроводности водонасыщенной породы; U — температура; t — время; vx, vy, vz— проекции скорости фильтрации флюида на оси координат, Р (х, у, z, t) — интенсивность источников тепла; с, ρ и с0, ρ0— удельная теплоемкость и плотность жидкости и горной породы.
Для решения данных уравнений нужно, чтобы было известно распределение скоростей фильтрации.
Приведём уравнения фильтрации:
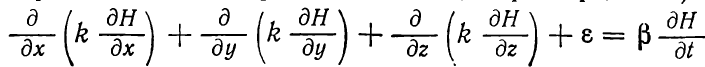 (1.3)
(1.3)
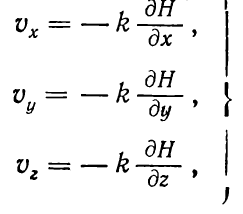 (1.4)
(1.4)
В уравнениях 1.3 и 1.4 приняты следующие обозначения: где k — коэффициент фильтрации; Н — напор; ε — интенсивность
источников жидкости; β — коэффициент упругоемкости водонасыщенных пород.
При решении конкретной задачи, чтобы получить однозначное решение, с помощью краевых решений на искомую функцию U или H накладываются дополнительные ограничения, которые позволяют учесть специфику каждой рассматриваемой задачи. Таким образом, решение задачи сводится к нахождению такой функции U, которая будет удовлетворять выбранным условиям.
Рассматривая задачу теплопереноса в водонапорных пластовых системах, следует её заметно упростить, учитывая их гидродинамические характеристики. Так процесс, который происходит в водоносном пласте, представляется возможным рассмотреть как двумерный. Следует пренебречь изменением температуры по высоте по оси z внутри пласта. Теплоперенос в слабопроницаемых породах, ограничивающих водоносные горизонты, принято считать кондуктивным.
Исходя из этих предположений можно переписать системы уравнений 1.1-1.4
следующим образом.
При теплопереносе в водоупорных породах, которые ограничивают водоносный пласт:
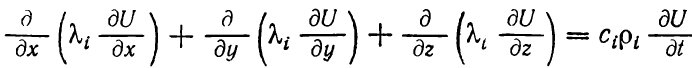 (1.5)
(1.5)
i = 1 для перекрывающих пород
i = 2 для подстилающих пород.
В
случае теплопереноса в водоносном
пласте
![]()
![]()
![]() (1.6)
(1.6)
В этих уравнениях qz1 и qz2 – тепловые потоки через кровлю и подошву пласта соответственно.
В свою очередь уравнение фильтрации записывается следующим образом:
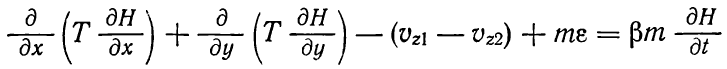 (1.7)
(1.7)
vz1 и vz2 скорость фильтрации через кровлю и подошву пласта;
Т = km — коэффициент водопроводимости; m — мощность пласта.
Перепишем уравнение (1.6) так:
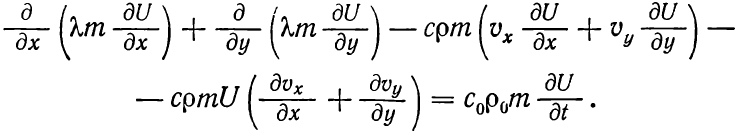 (1.8)
(1.8)
Упростим (1.8) исходя из несжимаемости жидкости и горных пород и отсутствии перетекания через кровлю и подошву уравнение (1.8):
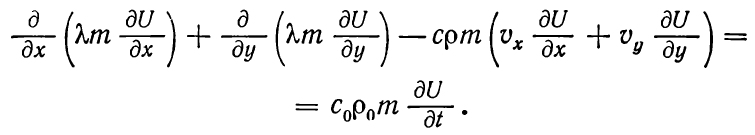 (1.9)
(1.9)
Учитывая упругий режим, запишем уравнение (1.8) с учетом уравнения (1.7):
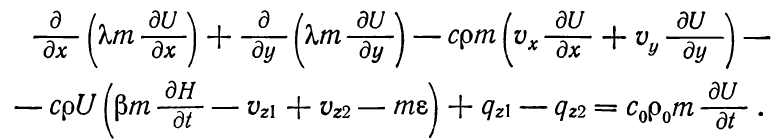 (1.10)
(1.10)
То, что температурное поле и тепловой поток непрерывны, задается на границе
водоносного пласта и водоупорных пород.
Таким образом с помощью системы уравнений (1.5), (1.6), (1.7) вместе с краевыми условиями, определяемые при постановке конкретной задачи, является моделью процесса нестационарного теплопереноса в пластовой водонапорной системе. Она показывает, как влияют изменения гидродинамических условий на то, как задается геотермического режима.
Члены, характеризующие тепловой поток через кровлю и подошву qz1, qz2, позволяют произвести учет теплообмена водоносного пласта и слабопроницаемыми толщами. В этом случае, осуществив решение системы уравнений (1.6) и (1.8), получают распределение температур в водоносном пласте. Если известно установившееся распределение скоростей фильтрации, то задача можно привести к решению уравнений (1.5) и (1.11).
Дополнительных упрощений задачи можно достигнуть, при допущении однородности водоносного пласта и постоянства мощности и того, что он залегает бесконечно глубоко. Также примем, что теплофизические свойства пород, которые покрывают и подстилают пласт, равны, скорость фильтрации считаем постоянной, процесс теплопереноса следует рассмотреть как одномерный.
Положим, что водоносный пласт мощностью m ограничивается плоскостями z = ± 4m. В этом случае температурное поле симметрично, так как мы считаем, что теплофизические характеристики подстилающих и перекрывающих водоносный пласт совпадают.
Существует расчетная схема, в ней породам, которыми окружен пласт, присуща конечная теплопроводность по вертикали и отсутствие теплопроводимости по горизонтали. В вертикальном направлении теплопроводность водоносного пласта бесконечно велика, из-за этого температура пласта не подвержена изменениям по высоте и равна нулю, если смотреть по горизонтальной плоскости. В этом случае процесс теплопереноса можно описать системой уравнений:
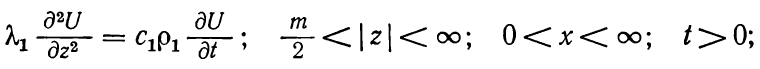 (1.11)
(1.11)
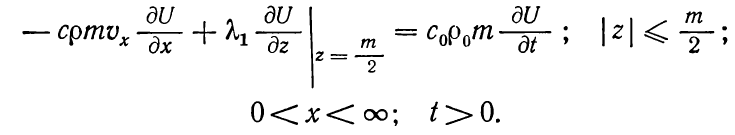 (1.12)
(1.12)
Рассмотренная выше схема носит имя X. А. Ловерье, по имени ученого, его предложившими.
Также существует альтернативная схема, предложенная Н.А. Авдониным. В ней есть существенные отличия от схемы Ловерье, а именно тем, что Авдониным был учтен кондуктивный теплоперенос в водоносном пласте по горизонтали, теплопроводность пласта в горизонтальном направлении считают конечной. При этом вместо уравнения (1.12) следует рассматривать уравнение
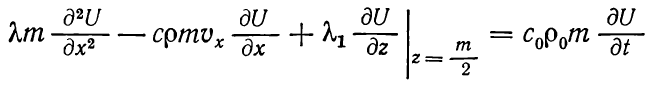 (1.13)
(1.13)
Если рассматривать распределение температуры лишь в водоносном пласте, то его можно получить, решив уравнение
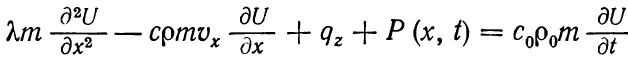 (1.14)
(1.14)
В этом уравнении с помощью qz происходит учет теплообмена водоносного пласта с окружающими породами.
В случае, когда перемещение жидкости в пласте определяет работающая скважина радиуса rc, течение осесимметричное. Тогда уравнение теплопереноса лучше записать в цилиндрических координатах. Заменим уравнения (1.5) и (1.9) на уравнения
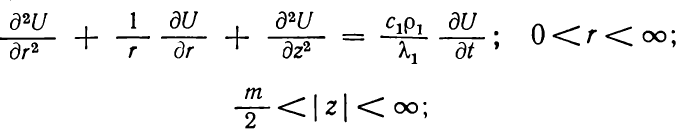 (1.15)
(1.15)
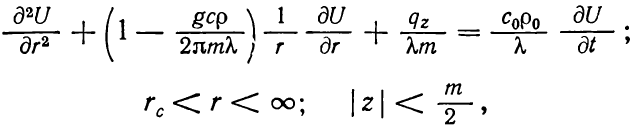 (1.16)
(1.16)
Где
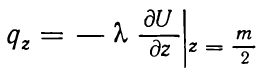 —
тепловой поток через кровлю и подошву
—
тепловой поток через кровлю и подошву
водоносного пласта, q — дебит скважины.
Для условий схемы X. А. Ловерье система уравнений (1.15) и
(1.16) принимает вид
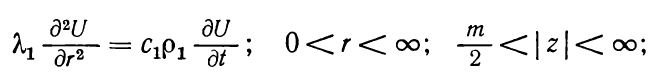 (1.17)
(1.17)
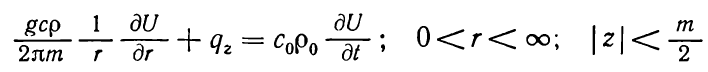 (1.18)
(1.18)
Расчетная схема Н. А. Авдонина («неполная схема
сосредоточенной емкости») отличает следующее: уравнение (1.18) заменяется на уравнение, которое учитывает кондукцию в водоносном пласте – уравнение (1.16).
Происходящие в естественных условиях можно считать установившимися, а также распределение температуры зависит от температуры смежных пластов или поверхности Земли. В данной ситуации будет слишком грубым допущение, что пласт залегает бесконечно глубоко. По этой причине при рассмотрении стационарной задачи учитываются данные положения.
АНАЛИТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА НЕСТАЦИОНАРНОГО
ТЕПЛОПЕРЕНОСА.
Приведем здесь рассмотрение некоторых аналитических решений, которые можно применять при изучении процессов теплопереноса подземными флюидами.
При независимости теплообмена пласта с окружающими породам от координат и времени:
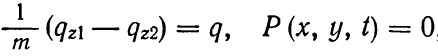
и решение уравнения при краевых условиях
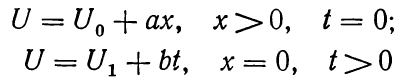 (1.19)
(1.19)
Записывается как
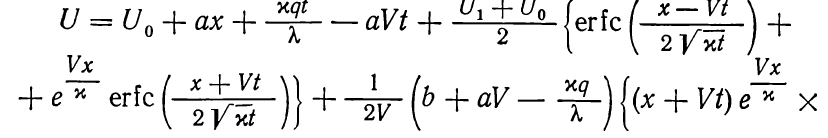
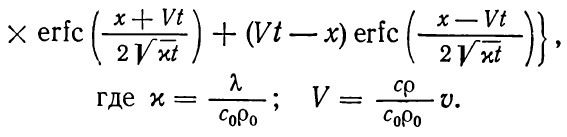 (1.20)
(1.20)
При постоянной начальной температуре изолированного пласта
![]()
и зависимом от температуры кондуктивном тепловом потоке
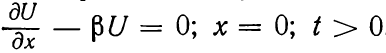
решение можно представить следующим образом:
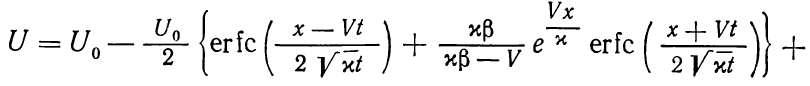
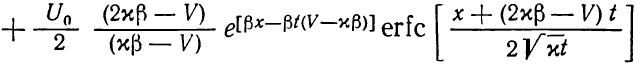 (1.21)
(1.21)
При
изменении температуры на границе
теплоизолированного пласта х = 0,
происходящем по закону
![]() ,
стационарное
,
стационарное
решение,
которое ограничено при
![]() ,
можно записать так
,
можно записать так
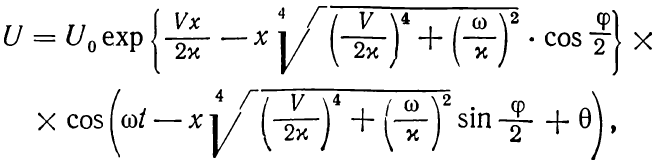 (1.22)
(1.22)
где
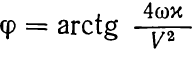
Когда работает скважина, следует обратиться к случаю радиального течения в теплоизолированном пласте. В этом случае процесс теплопереноса описывается с помощью уравнения (1.16)
Если
начальная температура равна нулю, а
граничное условие имеет вид
![]() ,
,
то решение уравнения (1.16) записывается следующим образом:
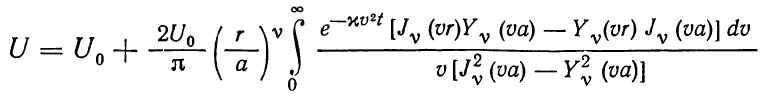
Где
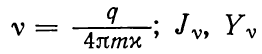 —функции
Бесселя первого и второго рода
соответственно.
—функции
Бесселя первого и второго рода
соответственно.
Происходит рассмотрение теплопереноса в ограниченном участке
водоносного пласта 0 < х < l начальной температурой U = 0,
t= 0; на границе с окружающими породами, которые имеют нулевую
температуру,
осуществляется теплообмен, коэффициент
теплообмена
![]() .
.
Запишем тепловой поток через единицу площади кровли и подошвы пласта
![]()
граничные условия записывается так:
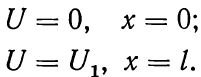
В этом случае решение уравнения (1.14), учитывая (1.24), можно записать так: