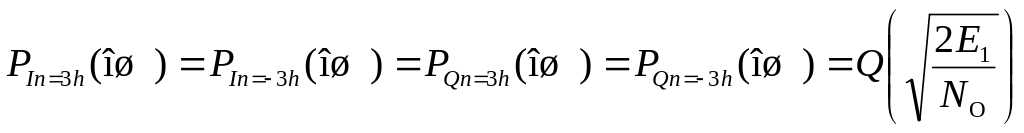3.7. Демодулятор

Когерентный демодулятор производит анализ принятого приёмником колебания z(t) = μs_КАМ(t) + n(t), сопоставляя его с известными образцами сигналов, формируемых модулятором. Анализ завершается принятием решения по критерию максимального правдоподобия в пользу наиболее вероятного передаваемого сигнала (символа).

Требуется:

1. Изобразить структурную схему когерентного демодулятора,

оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции.

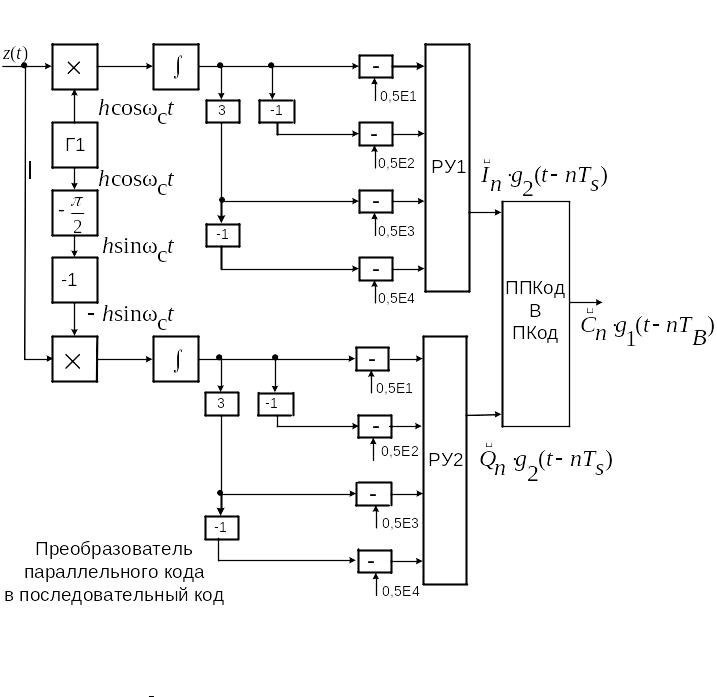
Рис. 30 Схема демодулятора для сигнала квадратурной модуляции КАМ-16

2. Написать алгоритмы работы решающих устройств РУ1 и РУ2 в

составе когерентного демодулятора.

.

В момент окончания каждого символьного интервала длительностью решающее устройство РУ1 (и РУ2) определяет номер входа , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате:

«00» при = 1, «10» при = 2, «01» при = 3, «11» при = 4.

3. Определить вероятности ошибок на выходах РУ1 и РУ2 при определении значений символов I_n и Q_n, равныхh, –h, 3h, –3h(табл. 3) [2]:

,

,

где P_In=x(ош) иP_Qn=x(ош)­– вероятности ошибочного приемапри I_n=x и Q_n=x, соответственно,

Таблица 3

Передаваемые величиныIn и Qn	Вероятность ошибки в работе РУ1 и РУ2
In= ±h,Qn= ±h	, где Q(x)– дополнительная функция ошибок, Е1 - энергия сигнала 1·cosωct, Е1 = 0,5·12·TS NO – спектральная плотность мощности БГШ
In= ±3h,Qn= ±3h

=

=

E₁ = 0,5h²T_S =

4. Определить вероятности ошибок на выходе преобразователя

параллельного кода в последовательный код (ФМС) для заданных параметров сигналов и [2]:

для точек сигнального созвездия с координатами I_n= ±h,Q_n= ±h (4 точки у QPSKи у QASK)

P_In=h,Qn=h(ош) = P_In=h(ош) + P_Qn=h(ош) – P_In=h(ош)·P_Qn=h(ош),

для точек сигнального созвездия с координатами I_n= ±3h,Q_n= ±3h(4 точки только у QASK)

P_In=3h,Qn=3h(ош) = P_In=3h(ош) + P_Qn=3h(ош) – P_In=3h(ош)·P_Qn=3h(ош),

для точек сигнального созвездия с координатами I_n= ±3h,Q_n= ±h и I_n= ±h,Q_n= ±3h(8 точек только у QASK)

P_In=3h,Qn=h(ош) = P_In=3h(ош) + P_Qn=h(ош) – P_In=3h(ош)·P_Qn=h(ош).

5. Определить среднюю вероятность ошибки на выходе преобразователя:

для QPSK:

P_ср(ош) =4·P_In=h,Qn=h(ош) / 4 = P_In=h,Qn=h(ош),

для QASK:

P_ср(ош) =[4·P_In=h,Qn=h(ош) + 4·P_In=3h,Qn=3h(ош)+ 8·P_In=3h,Qn=h(ош)] / 16.

3.8 Декодер

Декодер формирует из непрерывной последовательности кодовых символов, поступающих с выхода демодулятора (возможно, с ошибками), выходную непрерывную последовательность декодированных кодовых символов, в которых ошибки частично либо полностью исправлены.

Требуется:

1. Изучить алгоритм сверточного декодирования по методу Витерби [1, с. 253-256].

2.Переписать последовательность кодовых символов, полученных на выходе кодера из п. 4 раздела 3.3

c(iT_b) = 110110101001001011.

3. Получить входную для декодера последовательность кодовых символов ĉ_ВХ(iT_b) путём внесения в последовательность c(iT_b) однократной ошибки в позиции q (по варианту)

ĉ_ВХ(iT_b)= 010110101001001011(при q = 1).

4.Построить решетчатые диаграммы выживших путей декодера для интервалов: t₁–t₄, t₁–t₅, t₁–t₆, t₁–t₇, t₁–t₈, t₁–t₉, t₁–t₁₀, t₁–t₁₁ (рис. 3.8.1).На построенных диаграммах, вычислить метрики путей, входящих в каждый узел диаграммы, выделить фрагменты единственно выживших путей и прочитать по ним декодированную кодовую последовательность ĉ_ВЫХ(iT_b). Убедиться в том, что ĉ_ВЫХ(iT_b) = c(iT_b), т.е. в исправлении ошибки в позиции q.

Рис. 3.8.1, а. Диаграмма декодера на интервале t₁–t₄

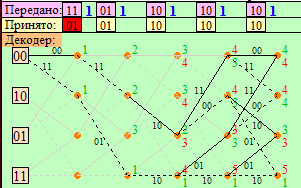
Рис. 3.8.1, б. Диаграмма декодера на интервале t₁–t₅

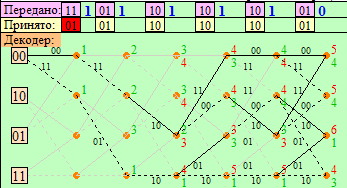
Рис. 3.8.1, в. Диаграмма декодера на интервале t₁–t₆

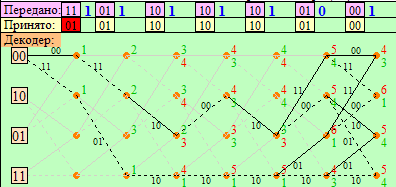
Рис. 3.8.1, г. Диаграмма декодера на интервале t₁–t₇

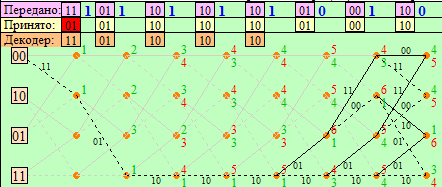
Рис. 3.8.1, д. Диаграмма декодера на интервале t₁–t₈

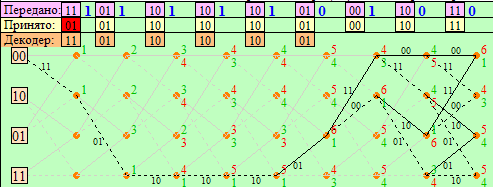
Рис. 3.8.1, е. Диаграмма декодера на интервале t₁–t₉

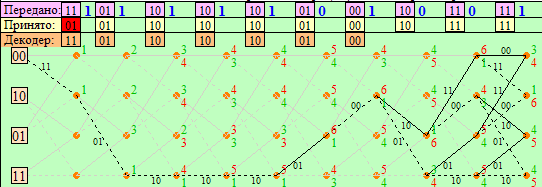
Рис. 3.8.1, ж. Диаграмма декодера на интервале t₁–t₁₀

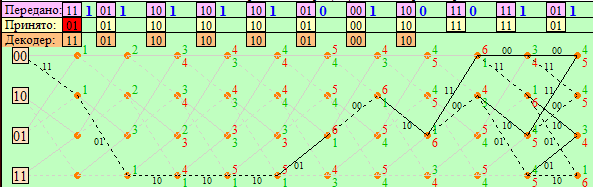
Рис. 3.8.1, з. Диаграмма декодера на интервале t₁–t₁₁

ЛИТЕРАТУРА

1. Сальников А.П. Теория электрической связи: Конспект лекций / СПбГУТ. – СПб., 2007. – 273 с.: ил.

2. Общая теория связи: методические указания к выполнению курсовой работы / Л. Н. Куликов, М. Н. Москалец, М. Н. Чесноков. – СПб. : Издательство СПбГУТ, 2012. – 80 с.

Дополнительные рекомендации по оформлению КР:

Основной текст печатается на одной стороне листа с выравниванием по ширине (TimesNewRoman, 12 пт, обычный, межстрочный интервал одинарный; абзацный отступ – 1 см).

Поля: верхнее – 2,5 см, нижнее – 3 см, левое – 2,5 см, правое – 2 см.

Не допускается использование табуляции или пробелов для формирования отступа первой строки. Страницы нумеруются.

Рисунки размещаются после ссылок на них, нумеруются внутри разделов и снабжаются подрисуночными надписями. В тексте на них должны быть ссылки.

Для обозначения переменных в формулах и в тексте используют курсив, если буквы из латиницы, и обычный шрифт для кириллицы и греческого алфавита.

При наличии списка литературы, в тексте должны быть ссылки на источники.

Готовая работа сшивается в виде тетради. Использование файликов для вложения листов не допускается.

Сдача КР - 15 неделя

Любые отклонения от исходных данных по варианту рассматриваются как ошибка!