3.5. Модулятор

В состав модулятора входят блоки:

- генератор несущего колебания Ucosω_Сt,

- фазовращатель на – 90º для получения квадратурного несущего колебания Usinω_Сt,

- перемножители, для получения БМ сигналов S_I(t) =I(t)cosω_Сtи S_Q(t) =Q(t)sinω_Сt, модулированных сигналами I(t) и Q(t), соответственно;

- сумматор для получения сигнала с квадратурной модуляцией

S_КАМ(t)= S_I(t) +S_Q(t) = I(t)cosω_Сt + Q(t)sinω_Сt =

= A(t)cos(ω_Сt – ψ) = A(t)cos(ω_Сt + φ),

где –огибающая, а φ = (–ψ)– фаза сигнала S_КАМ(t);

cosψ = I(t)/A(t) = cosφ, sinψ = Q(t)/A(t) = –sinφ.

Требуется:

1. На четырех символьных интервалах T_S нарисовать графики следующих сигналов (в виде символических прямоугольников с указанием их амплитуд и фаз, определенных по сигнальному созвездию заданного вида модуляции):

1) синфазного БМ сигнала ;

2) квадратурного БМ сигнала ;

3) сигнала заданной квадратурной модуляции ;

4) кодовой последовательности с выхода кодера (без учета их временных сдвигов для удобства сопоставления). Графики указанных сигналов приведены на рис. 3.5.1.

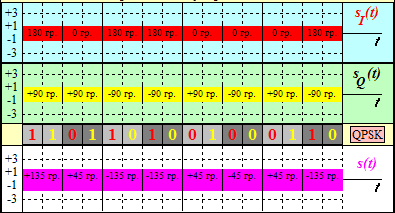
Рис. 3.5.1. Графики модулированных сигналов s_I(t), s_Q(t) и s_КАМ(t) (для QPSKвар. 02)

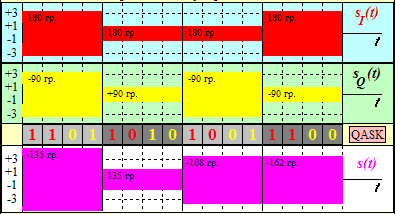
Рис. 3.5.1. Графики модулированных сигналов s_I(t), s_Q(t) и s_КАМ(t) (для QASKвар. 01)

2. Написать аналитические выражения для корреляционных функций B_SI(τ), B_SQ(τ)и для спектральных плотностей мощности G_SI(f) и G_SQ(f) сигналов S_I(t) иS_Q(t) на выходах перемножителей модулятора.

Из анализа, приведенного в [2, стр. 41 – 42], следует

,

аналогично

Спектральные плотности мощностиG_SI(f)и G_SQ(f)сигналов S_I(t) иS_Q(t) можно найти по теореме Винера-Хинчина как преобразование Фурье от их корреляционных функций [2, стр.43]

,

.

3. Написать аналитические выражения для корреляционной функции сигнала B_S(τ) и для спектральной плотности мощности G_S(f) сигнала S_КАМ(t) заданного вида квадратурной модуляции на выходесумматора модулятора. Построить графики этих функций.

Учитывая, что процесс S_КАМ(t) является суммой двух случайных независимых процессовS_I(t) иS_Q(t)

S_КАМ(t)= S_I(t) +S_Q(t) = I(t)cosω_Сt + Q(t)sinω_Сt,

его корреляционная функция будет равна сумме корреляционных функций слагаемых процессов

B_S(τ) = B_SI(τ) +B_SQ(τ) =

По этой же причине спектральная плотность мощности G_S(f) сигнала S_КАМ(t) есть сумма энергетических спектров G_SI(f)и G_SQ(f) сигналовS_I(t) иS_Q(t), соответственно,

.

Графики B_S(τ) и G_S(f) приведены на рис. 5.3.2.

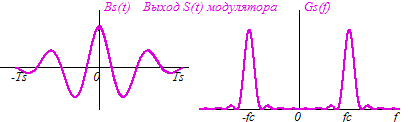
Рис. 5.3.2. Графики корреляционной функции B_S(τ) и энергетического спектра G_S(f)

4. ОпределитьF_S –ширину спектрамодулированного сигналаS_КАМ(t)по второму нулю его огибающей

3.6. Непрерывный канал

Передача сигнала s_КАМ(t)происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии

аддитивной помехи типа гауссовского белого шума (АБГШ). Сигнал на выходе такого канала имеет вид

z(t) = μs_КАМ(t) + n(t),

где μ – коэффициент передачи канала. Для всех вариантовпринять μ = 1. Односторонняя спектральная плотность мощности помехи равна N_О

(значения N_О для своего варианта взять из таблицы исходных данных).

Требуется:

1. Определить минимально необходимую ширину полосы частот непрерывного канала F_К.

F_К = F_S =

2. Определить мощность помехи на выходе канала.

Р_П = N_O·F_К =

3. Определить P_C­ среднюю мощность сигнала s(t) и найти отношениеP_C / P_П.

(вар. четный) (вар. нечетный)

(вар. 0)

4. Рассчитать пропускную способность (за секунду) непрерывного канала

5. Оценить эффективность использования пропускной способности непрерывного канала.

где