
- •Энергетические методы определения перемещений
- •Работа внешних сил при изгибе
- •Обобщенная работа внешних сил
- •Потенциальная энергия деформации при растяжении стержня
- •Потенциальная энергия деформации при
- •Потенциальная энергия деформации при чистом изгибе балки
- •Потенциальная энергия бруса при сложном нагружении
- •Теорема Кастилиано (продолжение)
- •Пример применения теоремы Кастилиано
- •Пример применения теоремы Кастилиано (метод фиктивной силы)
- •Интеграл Мора
- •Интеграл Мора (продолжение)
- •Применение интеграла Мора
- •Применение интеграла Мора (продолжение 1)
- •Применение интеграла Мора (продолжение 2)
- •Применение интеграла Мора (продолжение 3)
- •Применение интеграла Мора (продолжение 4)
- •Применение интеграла Мора (продолжение 5)
- •Применение интеграла Мора (продолжение 6)
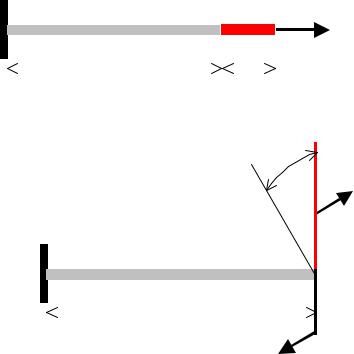
Энергетические методы определения перемещений
Работа внешних сил
Растяжение-сжатие
|
|
|
PX |
AP |
1 PX L |
|
|
|
|||
|
|
|
|||
|
L |
dL |
|||
|
|||||
|
|
|
X |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
Кручение
|
|
φ |
|
|
|
|
|
|
|
|
MX |
A |
1 M |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
M X |
2 |
X |
|
|
L |
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
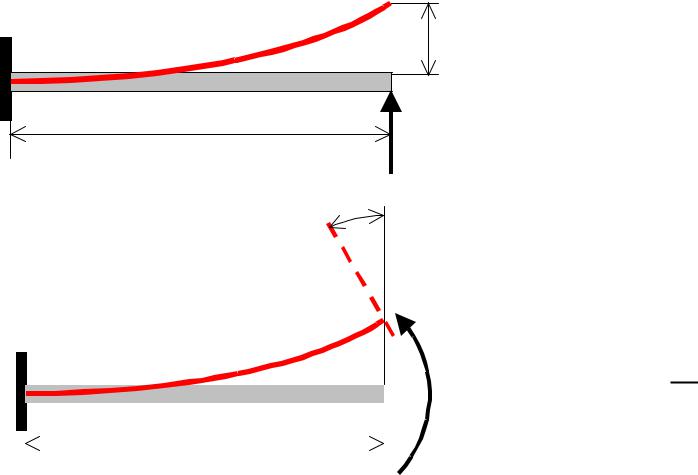
Работа внешних сил при изгибе
δ
L |
AP |
1 PY |
PY |
Y |
2 |
|
|
|
θ |
|
|
|
|
A |
1 |
M |
|
|
|||
|
|
MZ MZ |
2 |
Z |
|
L |
|||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Обобщенная работа внешних сил
Ф орм улы м ож н о обобщ ить
APОБ 12 PОБ ОБ
где Р О Б – обобщ енная сила, т.е. лю бое силовое воздей стви е, лю бой си ловой ф актор;
δО Б - обобщ ен ное перем ещ ен ие, т.е. тот вид перем ещ ен ия, на котором Р О Б соверш ает работу.
К аж ды й из ш ести известны х силовы х ф акторов соверш ает работу на своем перем ещ ении
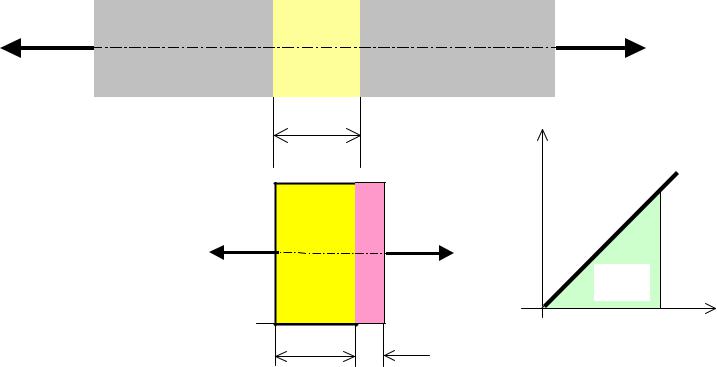
Потенциальная энергия деформации при растяжении стержня
PX |
|
|
|
PX |
|
|
|
||
|
|
|
|
|
dx
NX |
NX |
dx |
δx |
dU 1 |
N X x |
x N X dx |
U N X |
2 |
|
EF |
|
NX |
|
|
|
|
dU |
|
|
δx |
|
N X2 x dx |
|
|
2EF |
|
|
||
L |
|
|
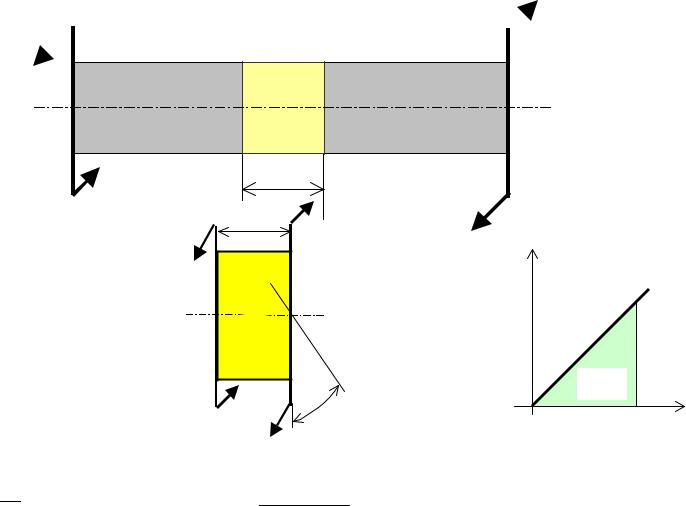
Потенциальная энергия деформации при
кручении вала
MK 
 MK
MK
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
MX |
|
MX |
|
|
|
|
|
|
|
|
|
|
|
dφ |
|
|
|
dU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δφ |
dU 1 M Xd |
d M X dx |
UM X |
|
M X2 |
x dx |
|
2 |
GI p |
|
2GI p |
|||
|
|
|
L |
|
||
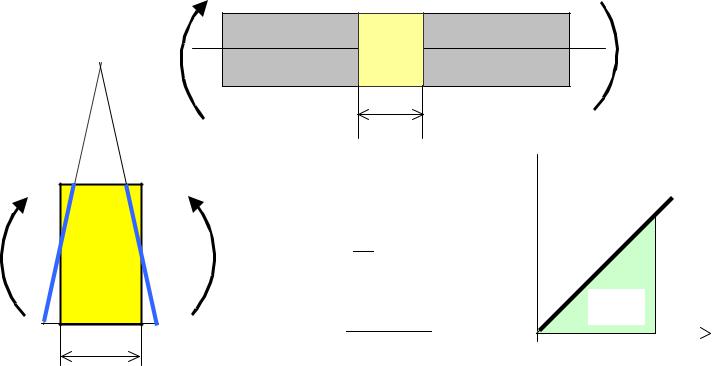
Потенциальная энергия деформации при чистом изгибе балки
dφ
MZ
dx
MZ  MZ
MZ
dx |
MZ  MZ
MZ
dU 12 MZd
d MZ dx |
dU |
|
|
||
EIZ |
|
dφ |
|
||
|
|
|
UMZ |
M Z2 x dx |
UMY |
MY2 x dx |
|
L 2EIZ |
|
L 2EIY |
Потенциальная энергия бруса при сложном нагружении
К |
а ж д о м |
у |
|
с и л о в о м |
у |
ф |
а к т о р у |
с о о т в е т с т в у ю т |
п е р е м |
е щ |
е н и я , н а |
||||||||||
к о т о р ы |
х |
о с т а л ь н ы |
е |
с и л о в ы е |
ф а к т о р ы |
н е |
с о в е р ш а ю |
т |
р а б о т у . |
||||||||||||
П |
о э т о м |
у |
п о т е н ц и а л ь н а я |
э н е р г и я |
д е ф |
о р м |
а ц и и |
п р и |
с л о ж н о м |
||||||||||||
н а г р у ж |
е н и и |
р а в н а |
|
с у м |
м |
е |
п о т е н ц и а л ь н ы х |
э н е р г и й |
ш |
е с т и |
о т д е л ь н ы х |
||||||||||
ф |
а к т о р о в . |
П |
р е н е б р е г а я |
э н е р г и е й |
д е ф |
о р м |
а ц и и , |
с в я з а н н о й |
с |
||||||||||||
п о п е р е ч н ы |
м |
и |
с и л а м и , п о л у ч а е м |
д л я |
п о л н о й |
|
э н е р г и и |
д е ф |
о р м а ц и и |
||||||||||||
|
|
|
U |
|
U N X |
U |
M |
X |
U M Y |
U M |
Z |
, |
|
|
|
|
|||||
U |
|
|
N |
X2 x |
dx |
|
|
M |
X2 |
x |
dx |
|
|
M |
Y2 |
x |
dx |
|
|
M |
Z2 |
x |
|
dx |
|
|
2 EF |
|
|
2 GI |
|
p |
|
2 EI |
|
Y |
|
2 EI |
|
Z |
|
. |
|||||||||
|
|
L |
|
|
|
L |
|
|
|
L |
|
|
|
L |
|
|
|
|
|||||||
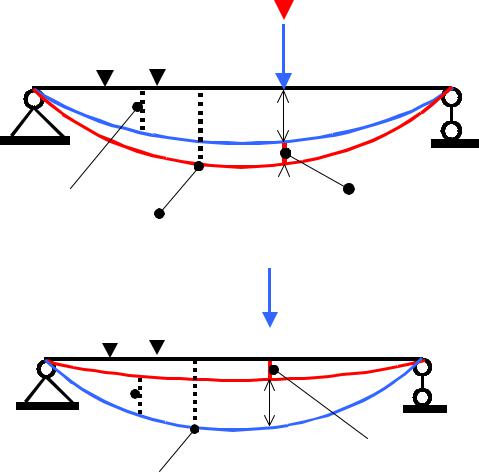
P1  P2
P2
U1 
U2
P1  P2
P2
U1 
U2 
Теорема Кастилиано
 dPn
dPn
Pn
|
dVn |
U |
|
U |
|
|
U |
dP |
|
|
2 |
1 |
|||||
|
|
|
||||||
|
|
|
|
|
|
n |
||
Pn |
|
|
|
|
|
Pn |
||
|
|
|
|
|
|
|
||
 dPn
dPn
 dVn
dVn
U2 12 dPndVn U1 dPnVn

Теорема Кастилиано (продолжение)
|
U 1 |
|
U dP dPdVU dPV |
||
1 |
P n 2 n n 1 |
nn |
|
n |
. |
|
|
|
1 dPdV
Пренебрегаячленомвторогопорядкамалости2 n n,получаем аналитическуюформулировкутеоремыКастилиано
U U
V V
n или ОБ
P P
n ОБ
Частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы вдоль направления действия этой силы.

Пример применения теоремы Кастилиано
|
M |
|||
O |
|
|
|
x |
|
|
A |
||
|
|
|
||
|
L |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Требуется найти угол поворота сечения θA и прогиб конца балки δA .
|
|
|
|
M Z2 x dx |
1 M 2L |
|
MZ (x) = M = const |
|
|
U L |
2EIZ |
2 EIZ |
|
А |
U |
|
ML |
|
|
|
M |
EIZ |
|
|
|||
|
|
|
|
|||
Но как найти прогиб конца балки δA ?
