Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

Лекция 1

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

655.94 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Курс математического анализа (ВМ 1) (1 семестр)

17 лекций (34 час)

25 практических занятий (50 час)

Рекомендуемая литература:

1.Курс высшей математики. Введение в математический анализ. Дифференциальное исчисление. Лекции и практикум: Учебное пособие / Под общей редакцией Петрушко И.М.. - СПб: Издательство "Лань", 2005 - 288 с.

2.Бугров Я.С., Никольский С.М. Высшая математика в 3 т.: учебное пособие для вузов,

Т. 2. - М.: "Дрофа", 2005 г. - 512 с.

Лекция 1

Предел функции в точке

1. Логическая символика математического анализа

- квантор всеобщности - “для всех”, “каждый”;

- квантор существования – “существует”;

- “не существует”;

:- “который”, “такой, что”;

- логический символ следствия:

A B - “ из высказывания А следует B”;

- логический символ равносильности:

A B - “ высказывание А равносильно B”;

- логический символ конъюнкции: С A B -

“Высказывание С справедливо, когда справедливо А и справедливо В ”;

- логический символ дизъюнкции: С A B -

“Высказывание С справедливо, когда справедливо А или справедливо В

или справедливо А и В совместно”;
- логический символ строгой дизъюнкции:	С A B -

“Высказывание С справедливо, когда справедливо А или справедливо В”;

- логический символ принадлежности:	a A -
“элемент a принадлежит множеству	A ”;
- “не принадлежит”;

	3
- логический символ включения:	A B -

“множество A является подмножеством множества B ”;

- логический символ пересечения множеств:

СA B с С : c A c B ;

- логический символ объединения множеств:

С A B с С : c A c B ;

\- логический символ разности множеств:

СA \ B с С : c A c B ;

Примеры:

x R y R x y 5 - истина;

x R y R x y 5 - ложь;

A B a A a B b B b A;

A B a A a B b B b A.

2.Основные числовые множества

N 1, 2, 3, 4, 5,..., n,... - множество натуральных чисел;


Z	0,	1,	2,	3,	4,	5,..., z,... - множество целых чисел;
			z
Q q : q				-	множество рациональных чисел (бесконечные
Q q : q				-	множество рациональных чисел (бесконечные
			n

периодические дроби);

I - множество иррациональных чисел (бесконечные непериодические дроби);

R - множество действительных чисел ( Q R \ I );

N Z Q R.

На множестве действительных чисел выделим следующие числовые множества:

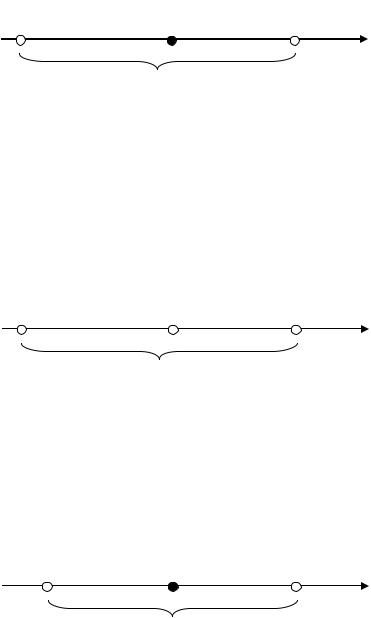
X1 a,b x X1,		X1 R : a x b - отрезок;
X2	a,b x X2	, X2	R : a x b - интервал;
X3	a,b x X3 , X3		R : a x b - полуинтервал;
X4	a,b x X 4	, X 4	R : a x b - полуинтервал.

3.	Окрестность точки.
Определение 1. Любой интервал, включающий в себя			точку x0 , будем
называть окрестностью точки x0 (обозначение - O x0 ).
a	x0	b	x

O( x0 )

Рис. 1.
Определение 2.	Окрестность точки	x0 , из которой искусственно удалена
(выколота) точка	x0 , будем называть проколотой		окрестностью точки x0
0
(обозначение - O x0 ).
a	x0	b	x

		O( x0 )
Рис. 2.
Определение 3.	Интервал	x0 ; x0 ,	где	0,	R , будем
называть дельта-окрестностью точки x0 (обозначение - x0 ).
		x0		x
	x0	x0	x0	x

( x0 )

Рис. 3.

		6
Определение 4. Интервал		x0 ; x0 ,	где 0,			R , из которого
искусственно удалена (выколота) точка x0 ,				будем	называть проколотой
дельта-окрестностью точки x0 (обозначение - 0				x0 ).
		x0				x
	x0	x0		x0		x

( x0 )

Рис. 4.

Определение 5. Точка x стремится к точке x0 слева (обозначение x x0 0 ), если значение x увеличивается, при этом выполняется условие: x x0 .

Рис. 5.
Определение 6.	Точка	x стремится к	точке x0	справа (обозначение
x x0 0 ), если	значение	x уменьшается,	при этом	выполняется условие:
x x0 .
		x0	x	x

Рис. 6.
Определение 7. Точка x стремится к точке x0			(обозначение x x0 ), если
выполняется условие: x x0 0	x x0 0
x	x0	x	x

Рис. 7.

4. Конечный предел функции в точке

Пусть в некоторой окрестности точки x0 в системе координат xOy определена функция у f (x) , за исключением может быть самой точки x0 .

Определение 8. Число a const называется пределом функции f (x) в точке x0 слева, если для любого положительного (сколь угодно малого) числа

0 существует		число		N R , такое, что из условия	N x x0			следует
			.
условие	f (x) a		.
Сокращенная запись:
a lim f (x) 0 N R : x N, x0						f (x) a	. (1)
a lim f (x) 0 N R : x N, x0						f (x) a	. (1)
	x x0 0
	x x0 0			a const называется пределом функции				f (x) в
Определение 9.		Число		a const называется пределом функции				f (x) в

точке x0 справа, если для любого положительного (сколь угодно малого) числа 0 существует число N R , такое, что из условия x0 x N следует условие f (x) a .

Сокращенная запись:

a lim

f (x) 0 N R : x x0 , N

f (x) a

(2)

x x0 0

Число a const

называется пределом функции f (x) в

Определение 10.

точке x0 , если выполняется условие

a a

a const .

(3)

Сокращенная запись:

a lim f (x) 0 >0 : x (x0 )

f (x) a

(4)

x x0

При выполнении любого из условий (3), (4) говорят, что в точке

существует конечный предел функции

f (x) .

Замечание 1.

качестве точки

может рассматриваться бесконечно

удаленная точка или . Тогда справедливы следующие определения.

Определение 11.

Число a const называется пределом функции

f (x) при

x , если для любого положительного (сколь угодно малого) числа

				8
0 существует число				N R , такое, что из условия	x N следует
			.
условие	f (x) a		.
Сокращенная запись:
a lim		f (x) 0 N R : x , N				f (x) a	. (5)
a lim		f (x) 0 N R : x , N				f (x) a	. (5)
	x		Число a const называется пределом функции f (x) при
Определение 12.			Число a const называется пределом функции f (x) при

x , если для любого положительного (сколь угодно малого) числа
0 существует число			N R , такое, что из условия	N x следует
		.
условие	f (x) a	.
Сокращенная запись:
a lim f (x) 0 N R : x N ,					f (x) a	. (6)
a lim f (x) 0 N R : x N ,					f (x) a	. (6)
	x

5.Методика вычисления предела функции в точке

1.По некоторому закону формируется последовательность приближений к точке x0 в области определения функции f (x) :

x1, x2 , x3 , ... , xn , ...,

lim xn x0 ;

2. Формируется соответствующая последовательность значений функции: f (x1 ), f (x2 ), f (x3 ), ... , f (xn ), ...

3. Если, независимо от закона приближения к точке x0 , из условия

lim x

следует lim f (x ) a , то число a

- предел функции

f (x) в точке x0 .

Пример 1.

Для f (x) 3x 2

найти lim f (x) .

x 1

Решение:

Пусть закон приближения к точке

1 дихотомия

(половинное

деление).

Слева

приближение

начнем

точки

x1 2

по закону

n 2,3, 4,...

Тогда

2n 1

n 1

Таблица 1

…

-2

-1,5

-1,25

-1,125

-1,0625

-1,03125

-1,01563

…

f (xn )

-4

-2,5

-1,75

-1,375

-1,1875

-1,09375

-1,04688

…

Имеем a	lim(3x				2) 1 или a				lim (3x 2) 1.
		n		n				x 1 0
		n						x 1 0
Справа приближение начнем с							точки x 0 по				закону x	x			1		,
Справа приближение начнем с							точки x 0 по				закону x	x		n 1	2n 1		,
									1		n				2n 1
									1		n
n 2,3, 4,...			. Тогда
													Таблица 2

n		1			2	3		4		5	6			7		…
xn		0			-0,5	-0,75		-0,875		-0,9375	-0,96875		-0,98438			…
f (xn )		2			0,5	-0,25		-0,625		-0,8125	-0,90625		-0,95313			…

Имеем a lim(3x		2) 1 или	a	lim (3x 2) 1.
n	n			x 1 0
n				x 1 0
Получим для данного закона приближения к точке x0					lim(3x 2) 1.
					x 1

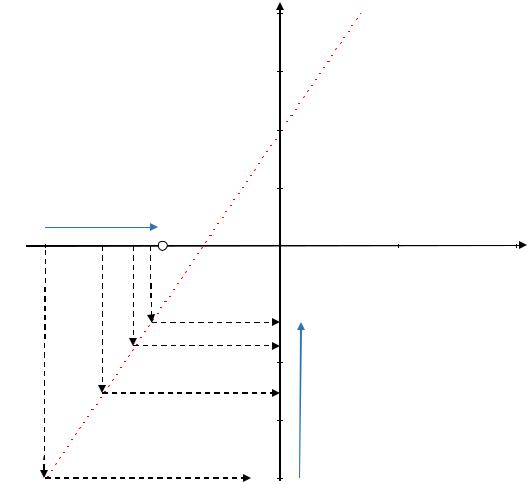
Графическая иллюстрация последовательности приближений к точке x0 для

функции f (x) 3x 2	представлена на		рис. 8.	Любой	другой	закон
приближения к точке	x0 1	для	данной	функции	дает	ответ:
lim 3x 2 1.
x 1

4	y

					x
f ( x)
f ( x)	2	1	0	1	2


			1

Рис. 8.

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции

#
16.05.2024655.94 Кб1Лекция 1.pdf
#
16.05.2024484.06 Кб0Лекция 10.pdf
#
16.05.2024483.36 Кб0Лекция 11.pdf
#
16.05.2024477.32 Кб0Лекция 12.pdf
#
16.05.2024265.24 Кб0Лекция 13.pdf
#
16.05.2024278.18 Кб0Лекция 14.pdf