ЛЕКЦИЯ 10.

ПОСТРОЕНИЕ РАЗНОСТНЫХ СХЕМ ДЛЯ СТАЦИОНАРНЫХ

ЗАДАЧ,

Материал также изложен в учебнике §15.2, §15.3, §15.4.

В лекции 9 рассматривался вопрос о решении краевой задачи:

найти функцию , удовлетворяющую дифференциальному уравнению второго порядка внутри отрезка и дополнительным (граничным) условиям в концах отрезка:

(10.1)

В предыдущей лекции были сформулированы основные теоремы о разрешимости, устойчивости и априорной оценке решения задачи (10.1) через входные данные

задачи. Была построена разностная схема в случае k(x)=1 .

Приведем еще раз разностную задачу для этого случая и будем ссылаться на нее как на задачу (10.2).

(10.2)

где ,

§ 10.1 Построение разностной схемы для уравнения с переменным

коэффициентом теплопроводности.

При решении задачи (10.1) наибольший интерес представляет случай, когда коэффициент теплопроводности является не константой, а функцией k(x),

и даже функцией, имеющей разрывы в точках отрезка [a,b]. Это соответствует тому случаю, когда стержень состоит, например, из различных физических материалов. По физическому смыслу функция u(x) – температура, поэтому она не может быть разрывной, функцией, также непрерывной функцией является функция - поток тепла в точке x.

Кажется удобным для построения разностной схемы предварительно преобразовать

уравнение (10.1), раскрыв внешнюю производную. Но как показали вычислительные эксперименты, такая схема является неустойчивой и вычисления нужно вести с очень маленьким шагом h. Рассмотрим другой подход к построению схемы.

Запишем уравнение (10.1), используя функцию :

Введем так называемые «полуцелые узлы»: точки . Обозначим

. Аппроксимируем производную потока тепла с помощью

центральной разностной производной, используя полуцелые точки:

Заметим, что центральная разностная производная имеет 2-ой порядок точности по h.

Теперь потоки в полуцелых точках заменим разностными аппроксимациями:

, и .

Тогда разностная схема примет вид:

(10.3)

, .

Можно доказать, что схема имеет 2-ой порядок аппроксимации и сходится

cо вторым порядком точности по h.

Разностную схему можно записать в матричном виде ,

Для этого преобразуем разностное уравнение следующим образом:

,

Очевидно, что матрица системы является трехдиагональной матрицей с диагональным

преобладанием элементов. Это означает, что система имеет единственное решение, которое может быть найдено методом прогонки. Запишем более подробно матрицу системы и правую часть системы уравнений.

, ,

, ,

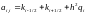Заметим, что матрица системы является трехдиагональной и обладает свойством диагонального преобладания. Система может быть решена методом прогонки.

§ 10.2 Метод баланса.

В случае, когда коэффициенты k, q и f имеют конечное число точек разрыва , i=1..M

решение краевой задачи уже нельзя понимать в классическом смысле. Уточним постановку задачи для уравнения с разрывными коэффициентами.

(10.4)

Назовем функцию u(x) решением задачи (10.4), если:

1) функция u(x) непрерывна на отрезке [a,b] и удовлетворяет краевым условиям:

u(a)=ua , u(b)=ub ;

2) поток непрерывен на отрезке [a,b] ;

3) всюду за исключением точек разрыва , i=1..M функция u(x) непрерывно дифференцируема и удовлетворяет уравнению:

(10.5)

Для вывода разностных уравнений воспользуемся методом баланса. Запишем уравнение теплового баланса для отрезка , i=1…N-1. Для этого проинтегрируем уравнение по x на указанном отрезке. В результате получим равенство:

Вычислим интеграл:

Воспользуемся приближенной формулой: и , разделив обе части равенства на шаг h , получим такое приближенное равенство:

Преобразуем формулы для потока тепла следующим образом.

Таким образом, получим:

,

где введено обозначение: - эффективное значение коэффициента

теплопроводности на отрезке . Величина называется коэффициентом теплового сопротивления отрезка. Перейдем теперь от приближенных равенств к разностному уравнению для нахождения приближенного решения :

i=1…N-1 (10.6)

, . (10.7)

Здесь , ,

Замечанния.

1. Разностные уравнения (10.6) записываются единообразно во всех внутренних узлах сетки независимо от того, где расположены точки разрыва коэффициентов дифференциального уравнения. Такие схемы называются однородными разностными схемами.

2. Если коэффициенты равны константам, то эта схема переходит в схему (10.2).