ЛЕКЦИЯ 12. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
ЛИТЕРАТУРА. Учебник [1] §§11.5, 11.8 - 11.10
[2] §§1,2
§12.1 Краткие сведения из предыдущей лекции.
ПОСТАНОВКА ЗАДАЧИ,
Пусть функция
задана
на множестве дискретных точек
,
,
…
,
предполагаем дополнительно, что
при
.
Задача интерполяции состоит в построении
функции
такой, что
,
.
Будем приближать функцию интерполяционным
многочленом
степени n.
ОПРЕДЕЛЕНИЕ. Многочлен
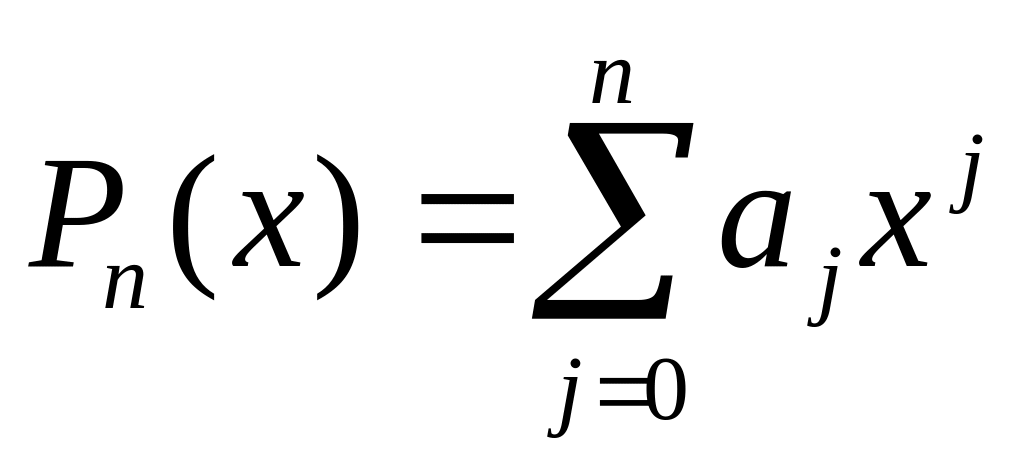степени n,
удовлетворяющий условию
,
называется интерполяционным многочленом.
ТЕОРЕМА 11.1. Интерполяционный многочлен существует и единственен.
Многочлен Лагранжа имеет следующего вид:
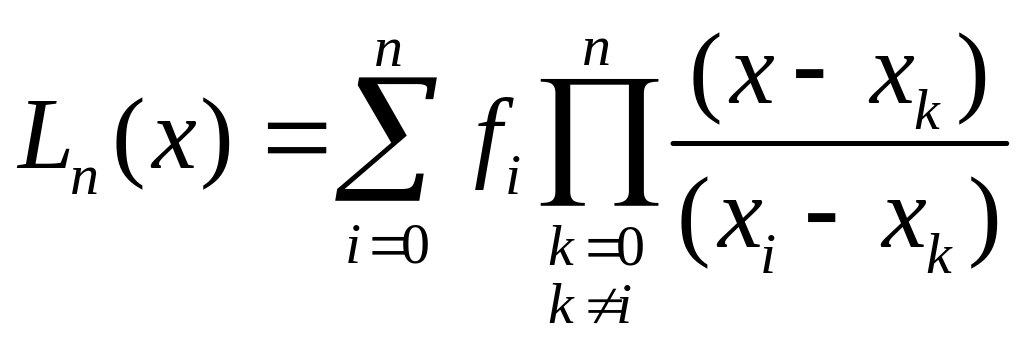(12.1)
ПОГРЕШНОСТЬ ИНТЕРПОЛЯЦИИ.
ОПРЕДЕЛЕНИЕ. Величина
называется
остаточным членом интерполяции.
Справедлива следующая теорема.
ТЕОРЕМА11.2. Пусть функция
дифференцируема (n+1)
раз на отрезке [a,b],
содержащем узлы интерполяции
.
Тогда для погрешности интерполяции в
точке
справедлива оценка:
(12.2)
Где
,
МНОГОЧЛЕН НЬЮТОНА С КОНЕЧНЫМИ РАЗНОСТЯМИ.
Пусть функция
задана
на множестве дискретных точек
,
,
…
значений аргумента с постоянным шагом
.
ОПРЕДЕЛЕНИЕ. Конечной разностью 1-го порядка называется величина
(12.3)
С помощью конечных разностей можно записать интерполяционный многочлен Ньютона с конечными разностями при интерполировании вперед.
(12.4)
ОПРЕДЕЛЕНИЕ . Величины
;
=
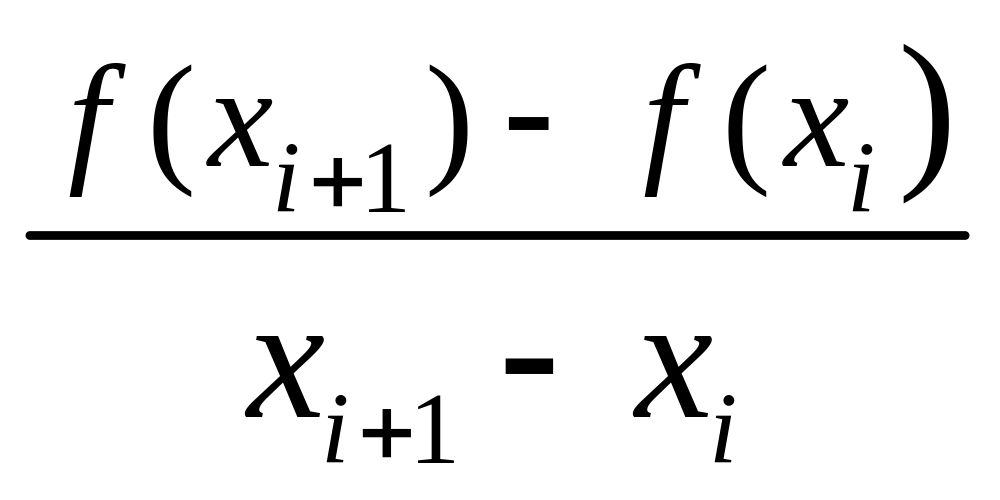(12.5)
называются разделенными разностями первого порядка. Разделенные разности второго порядка определяются формулой:
;
;
=
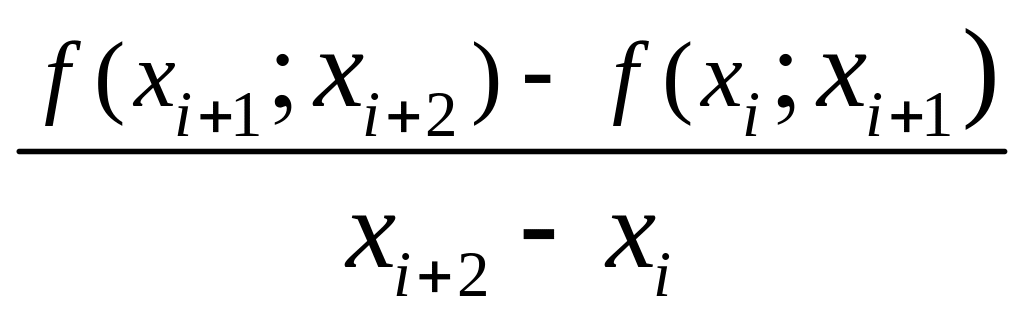(12.6)
Аналогично определяются разделенные
разности третьего и более высоких
порядков. Общее определение разделенной
разности порядка
таково:
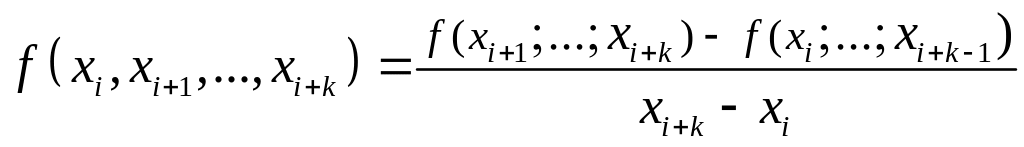(12.7)
Аналогично таблице конечных разностей строят таблицу разделенных разностей
§12.2. Кусочно-полиномиальная интерполяция.
Пусть функция интерполируется на отрезке [a,b].
Определение. Метод решения
задачи интерполяции единым для всего
отрезка многочленом
называют глобальной полиномиальной
интерполяцией.
Казалось бы хорошо иметь один многочлен, пригодный для приближения функции f во всех точках отрезка [a,b]. Однако существуют весьма веские причины, по которым глобальная интерполяция многочленами высокой степени, как правило, не используется.
1.Отсутствие сходимости при увеличении числа узлов.
Для того, чтобы реализовать процесс интерполяции функции многочленами все возрастающей степени n необходимо указать стратегию выбора при каждом n набора узлов.
n=0
n=1
n=2
……
Рассмотрим простейшую стратегию, состоящую в равномерном распределении узлов на отрезке [a,b] , то есть будем выбирать узлы интерполяции так:
(i=0,1,…n),
где
.
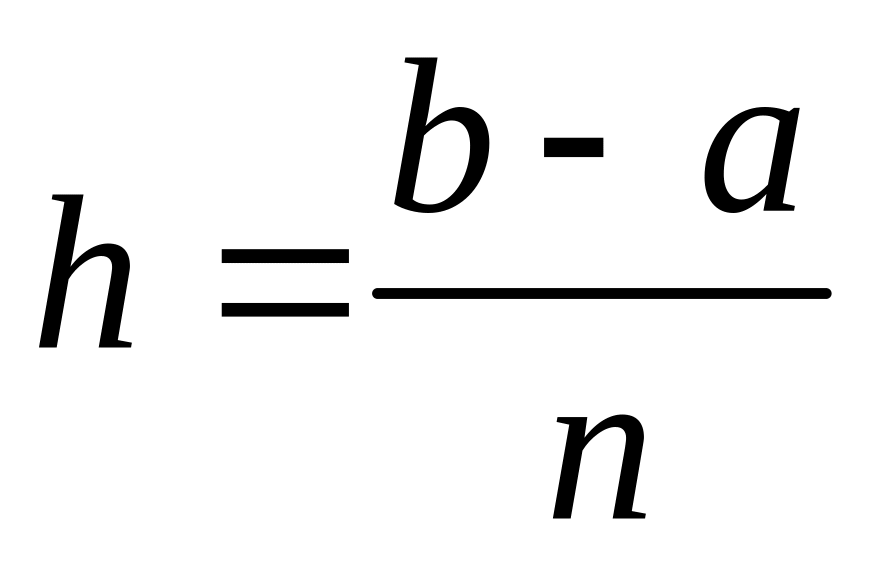Существует классический пример, показывающий, что такая стратегия не обеспечивает сходимости даже для бесконечно дифференцируемой функции.
ПРИМЕР 12.1 (функция Рунге). Будем приближать интерполяционным многочленом
на отрезке [-1,1] функцию
.
Вычисления показывают, что в центральной
части отрезка интерполяция при больших
n дает отличные результаты,
в то же время при
для
значений x:
наблюдается полиномиальное раскачивание.
ПРИЛОЖЕНИЕ 1.
Альтернативный подход состоит в
использовании локальной интерполяции,
когда функция интерполируется многочленом
невысокой степени на отрезке
малой
длины, содержащимся в [a,b].
При этом используется лишь часть
табличных значений.
ПРИЛОЖЕНИЕ 2.
ПРИМЕР.12.2. Функция y=y(x) задана таблицей своих значений:
x |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
y |
7 |
5 |
2.5 |
1.7 |
1.25 |
Требуется найти значения функции в точках 0.38, 0.7, 0.79
Построим диагональную таблицу конечных разностей:
0 7
-2
0.2 5 -0.5
-2.5 2.2
2.5 1.7 -3.55
-0.8 -1.35
0.6 1.7 0.35
-0.45
0.8 1.25
Рассмотрим интерполяцию локальными многочленами 2-ой степени:
,
при использовании на отрезке
.
Для точки x=0.38 имеет смысл взять в качестве узлов интерполяции точки 0.2, 0.4,0.6
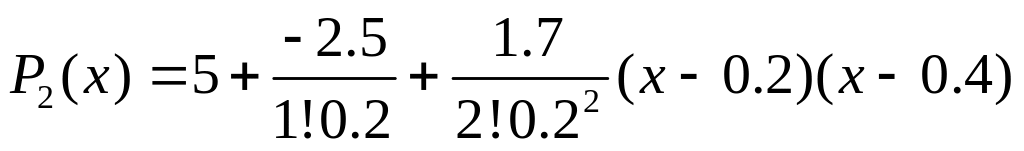
Для точек 0.7 и 0.79 можно использовать точки 0.4,0.6,0.8:
