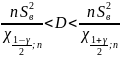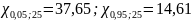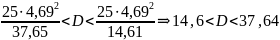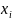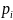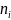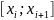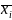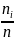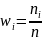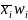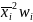Variant_7_bntu_tv
.docxВар. 7.
1. Из девяти значащих цифр составляются трехзначные числа. Сколько различных чисел может быть составлено?
Решение:
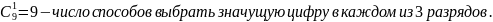
Общее число вариантов:
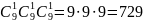
Ответ: 729
2. Из восьми книг две художественные. Найти вероятность того, что среди взятых наугад четырех книг хотя бы одна художественная.
Решение:
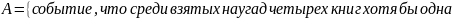
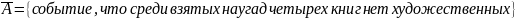
Для
вычисления вероятности события
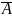применим формулу классической
вероятности:
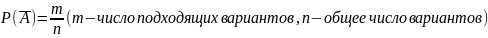
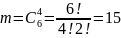
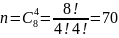
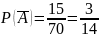
Так как сумма вероятностей противоположных событий равна 1, то
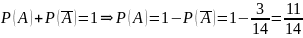
Ответ:
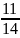
3. Вычислительная машина состоит из четырех блоков. Вероятность безотказной работы в течение времени Т первого блока равна 0,4, второго – 0,5, третьего – 0,6, четвертого – 0,4. Найти вероятность того, что в течение времени Т проработают: а) все четыре блока; б) три блока; в) менее трех блоков.
Решение:
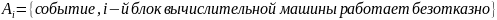
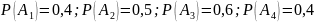
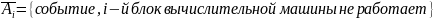
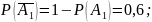
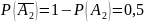
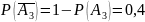
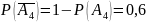
Найти вероятность того, что в течение времени Т проработают:
а) все четыре блока;
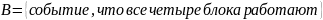
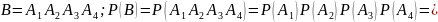
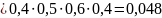
б) три блока;
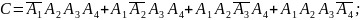
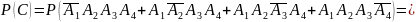
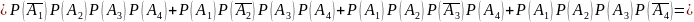
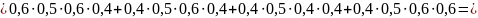
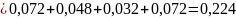
в) менее трех блоков
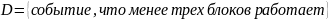
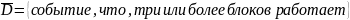
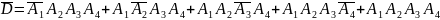
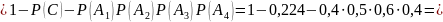
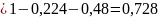
Ответ: а) 0,048;б)0,224; в)0,728
4. На двух станках обрабатываются однотипные детали. Вероятность брака для станка № 1 составляет 0,03, для станка № 2 – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на станке № 1, вдвое больше, чем на станке № 2. Найти вероятность того, что: а) взятая наугад деталь будет стандартной; б) наугад взятая стандартная деталь изготовлена на первом станке.
Решение:
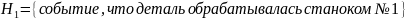
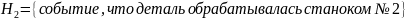
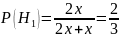
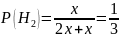
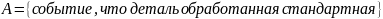
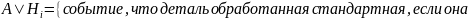
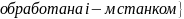
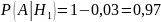
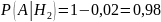
а) взятая наугад деталь будет стандартной;
применим формулу полной вероятности:
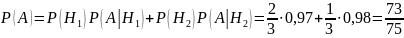
б) наугад взятая стандартная деталь изготовлена на первом станке.
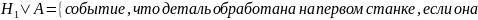
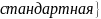
Применим формулу Байеса:
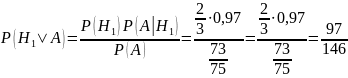
Ответ:
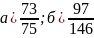
5. В телеателье имеется 7 телевизоров. Для каждого телевизора вероятность того, что в данный момент он включен, равна 0,6. Найти вероятность того, что в данный момент включены:, а) четыре телевизора; б) хотя бы один телевизор; в) не менее трех телевизоров.
Решение:
Применим для решения формулу Бернулли:
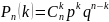
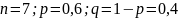
Найти вероятность того, что в данный момент включены: а) четыре телевизора;
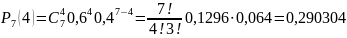
б) хотя бы один телевизор;
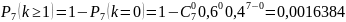
в) не менее трех телевизоров.
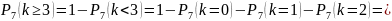
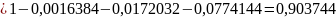
Ответ:
а)
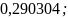б)
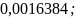в)
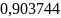
6.
Найти закон распределения указанной
дискретной СВ
и ее функцию распределения
.
Вычислить математическое ожидание
,
дисперсию
и среднее квадратичное отклонение
.
Построить график функции распределения
.
Вероятность поступления вызова на АТС в течение 1 мин равна 0,4; СВ – число вызовов, поступивших на АТС за 4 мин.
Решение:
Применим для решения формулу Бернулли:
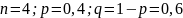
Составим закон распределения:
Случайная величина Х может принимать значения: X={0,1,2,3}
Вычислим соответствующие вероятности:
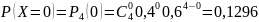
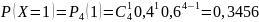
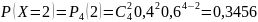
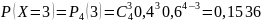
Запишем закон распределения:
|
0 |
1 |
2 |
3 |
4 |
|
0,1296 |
0,3456 |
0,3456 |
0,1536 |
0,0256 |
Запишем функцию распределения
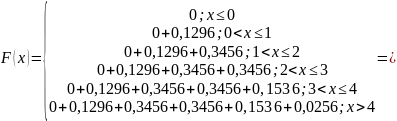
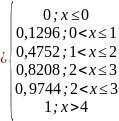
Вычислим математическое ожидание:
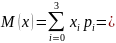
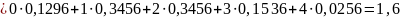
Вычислим дисперсию:
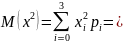
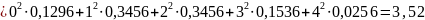
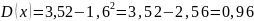
Вычислим среднее квадратическое отклонение:
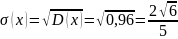
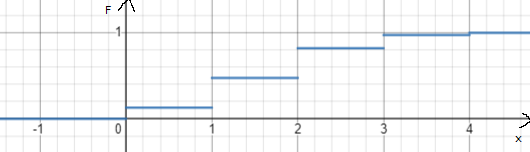
Строим график функции распределения:
7.
Дана функция распределения
СВ
.
Найти плотность распределения вероятностей
,
математическое ожидание
,
дисперсию
и вероятность попадания СВ
на отрезок
.
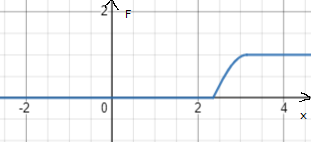
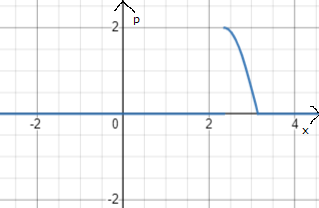
Построить графики функций
и
.
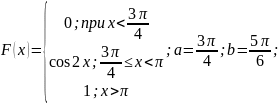
Решение:
Определим плотность распределения вероятностей:
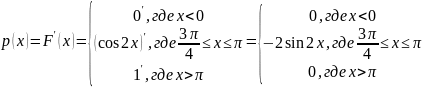
Вычислим
математическое ожидание
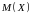
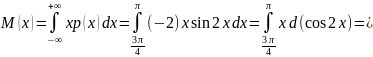
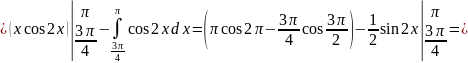
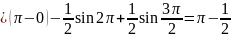
Вычислим
дисперсию
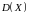
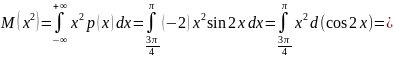
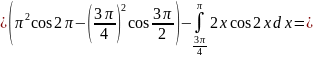
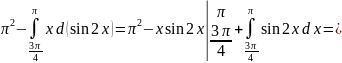
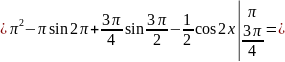
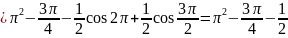
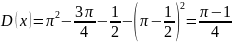
Вычислим вероятность
попадания СВ
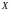на отрезок [
;
]
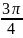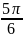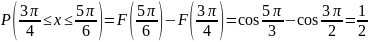
Строим графики
функци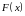й
и
8. В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:
а) записать значения результатов эксперимента в виде вариационного ряда;
б) найти размах варьирования и разбить его на 5 интервалов;
в) построить полигон частот, гистограмму относительных
частот и график эмпирической функции распределения;
г) найти числовые характеристики выборки хв, Dв;
д)
найти доверительные интервалы для
математического ожидания и среднего
квадратичного отклонения при надежности
.
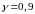28 |
22 |
30 |
15 |
24 |
26 |
35 |
28 |
22 |
20 |
15 |
22 |
24 |
26 |
30 |
24 |
30 |
32 |
28 |
18 |
28 |
22 |
26 |
24 |
30 |
Решение:
а) записать значения результатов эксперимента в виде вариационного ряда;
|
15 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
35 |
|
2 |
1 |
1 |
4 |
4 |
3 |
4 |
4 |
1 |
1 |
б) найти размах варьирования и разбить его на 5 интервалов;
|
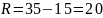
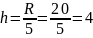
15-19 |
19-23 |
23-27 |
27-31 |
31-35 |
|
17 |
21 |
25 |
29 |
33 |
|
3 |
5 |
7 |
8 |
2 |
|
0,12 |
0,2 |
0,28 |
0,32 |
0,08 |
в) построить полигон частот, гистограмму относительных
частот и график эмпирической функции распределения;
Полигон частот:
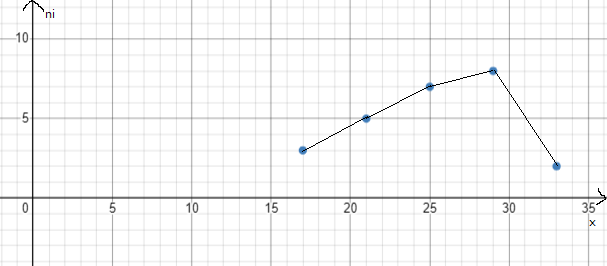
Гистограмму относительных частот:
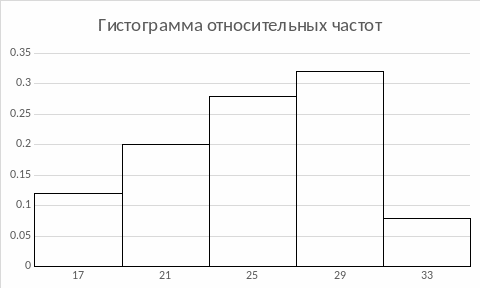
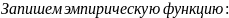
г) найти числовые характеристики выборки хв, Dв;
|
17 |
21 |
25 |
29 |
33 |
∑ |
|
0,12 |
0,2 |
0,28 |
0,32 |
0,08 |
1 |
|
2,04 |
4,2 |
7 |
9,28 |
2,64 |
25,16 |
|
34,68 |
88,2 |
175 |
269,12 |
87,12 |
654,12 |
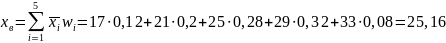
д) найти доверительные
интервалы для математического ожидания
и среднего квадратичного отклонения
при надежности
.
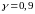Найдем доверительный интервал для математического ожидания
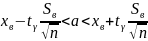
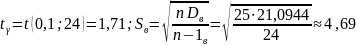
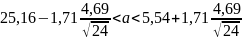
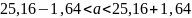
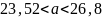
Найдем доверительный интервал для среднего квадратичного отклонения
