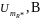для решения / ЛабЗ2
.docxЛабораторная работа №2. Экспериментальное определение модулей и аргументов комплексных сопротивлений.
Цель работы
1 Изучить частотные свойства простых линейных цепей.
2 Приобрести практические навыки в определении модулей и аргументов комплексных сопротивлений цепей с помощью радиоизмерительных приборов.
Содержание работы
1 Ознакомление с лабораторной установкой, измерительными приборами и методикой выполнения работы.
2 Выполнение предварительных теоретических расчетов для получения основных соотношений для обработки результатов измерений.
3 Экспериментальное определение модулей и аргументов комплексных сопротивлений указанных вариантов двухполюсников.
4 Обработка полученных результатов и оформление отчета.
Описание лабораторной установки
Лабораторная установка состоит из рабочей панели, генератора синусоидальных колебаний и двухлучевого осциллографа. Электрическая принципиальная схема установки, приведенная на рисунке 1.1, имеется и на рабочей панели установки. Кроме того, на панели установлены галетный переключатель на пять положений и тумблер на два положения, позволяющие коммутировать варианты двухполюсников.
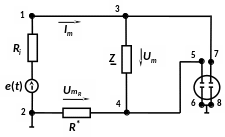
Рисунок 1.1
Генератор синусоидальных колебаний, вырабатывающий ЭДС e(t)=Em∙cosωt и обладающий некоторым внутренним сопротивлением Ri, подключается к гнездам 1, 2 на рабочей панели. Осциллограф подключается к гнездам 5, 6 и 7, 8. С помощью галетного переключателя и тумблера к гнездам 3, 4 подключаются различные варианты двухполюсника Z . Всего может быть 10 различных вариантов. Последний вариант «пустой», то есть в рабочей панели не содержится двухполюсника. В этом варианте может использоваться любой двухполюсник, подключенный к гнездам 3, 4.
Варианты схем двухполюсников, содержащихся в рабочей панели, приведены на рисунке 1.2.
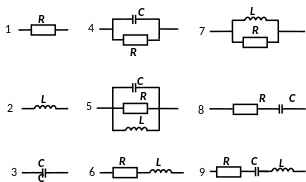
Рисунок 1.2
Резистор
R*,
содержащийся в схеме установки,
обеспечивает измерение косвенным путем
амплитуды тока Im
в
цепи исследуемого двухполюсника Z.
Измерив амплитуду напряжения на этом
вспомогательном резисторе
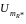 с помощью осциллографа, получим амплитуду
тока в цепи:
с помощью осциллографа, получим амплитуду
тока в цепи:
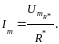 (1.1)
(1.1)
Активное сопротивление R*=10 Ом. Разность фаз между напряжением на двухполюснике и током в нем будет равна разности фаз между напряжением на двухполюснике и напряжением на вспомогательном резисторе
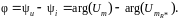 п (1.2)
п (1.2)
Используемый в лабораторной установке двухлучевой осциллограф позволяет определить комплексное сопротивление исследуемого двухполюсника для конкретной частоты ω:
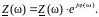 (1.3)
(1.3)
Модуль комплексного сопротивления определяется как отношение амплитуд напряжения и тока.
Измерение разности фаз между двумя гармоническими колебаниями производится по расстоянию между точками равных фаз по осциллограмме, показанной на рисунке 1.3.
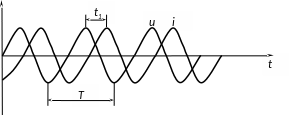
Рисунок 1.3
Так
как период гармонического колебания
равен
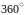 ,
то
,
то
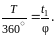
Из этой пропорции нетрудно вычислить φ.
При изменении частоты входного колебания исследуется зависимость модуля и аргумента комплексного сопротивления от частоты. Анализируя эти зависимости, можно сделать заключение о характере сопротивления двухполюсника, составе и виде соединения его элементов.
Методические рекомендации
При подготовке к выполнению экспериментальной части работы необходимо определить методику проведения исследований. Предварительные расчеты, выполненные на данном этапе, будут являться аналитической частью работы и позволят обосновать методику исследований. Целью этих расчетов является получение необходимых аналитических выражений для определения схемы исследуемого двухполюсника и параметров его элементов.
Рассмотрим в качестве примера двухполюсник, представляющий собой последовательное соединение элементов R, L, C (один из наиболее сложных случаев). При этом будем иметь в виду, что установка позволяет задавать разные значения частоты f или ω=2πf , измерять величины Im , Um , φ с помощью соотношений (1.1) – (1.3).
Вспомнив основные свойства R, L, C-цепи, заметим, что характерным ее признаком является резонанс напряжений на некоторой частоте ω0=2πf0. В этом случае фазовый сдвиг между напряжением и током становится равным нулю, а амплитуда тока становится максимальной. Значение этой частоты
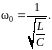 (1.4)
(1.4)
На резонансной частоте ХL=XC=0, а Z(ω)=R. Измерив с помощью осциллографа амплитуды напряжения Um (ω0) и тока Im(ω0) , получим активное сопротивление цепи:
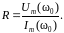 (1.5)
(1.5)
Изменив частоту генератора до некоторого значения ω1≠ ω0, получим величины Um (ω1), Im(ω1), φ(ω1). Реактивное сопротивление двухполюсника
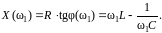 (1.6)
(1.6)
Используя соотношения (1.4) и (1.6), получим систему уравнений
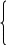
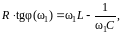 (1.7)
(1.7)
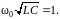
Решив эту систему, определим значения L и C .
Таким образом, при выполнении работы необходимо, кроме формул (1.1) – (1.4), подготовить расчетные соотношения, аналогичные формулам (1.6) – (1.7) для всех вариантов соединения элементов. При этом важно знать, как поведет себя та или иная цепь при изменении частоты входного колебания. Здесь нельзя обойтись без глубокого осмысления свойств исследуемого двухполюсника, в частности, зависимостей Z(ω) и φ(ω) от частоты.
Порядок выполнения работы
1 Подготовить лабораторную установку к работе. Собрать схему цепи, соответствующую рисунку 1.1, включить питание генератора и осциллографа.
2 Выполнить измерение на двух разных частотах амплитуд напряжения и тока, сдвига фаз между напряжением и током для исследуемого двухполюсника. С этой целью:
– установить требуемый уровень напряжения генератора и пределы измерений обоих каналов осциллографа;
– выбрать заданный вариант двухполюсника;
– выполнить измерения для каждого из вариантов и занести их в таблицу 1.1.
3 Определить состав элементов и характер их соединения, анализируя зависимости модуля и аргумента сопротивления от частоты.
4 Определить величины R, L, C исследуемых двухполюсников, пользуясь данными таблицы 1.1 и подготовленными расчетными соотношениями для всех вариантов. Заполнить таблицу 1.2.
Таблица 1.1
Вариант |
f, кГц |
Um, В |
|
Im, А |
φ, град. |
|
|
|
|
|
|
Таблица 1.2
Вариант |
Z, Ом |
R, Ом |
L, Гн |
C, Ф |
Характер соединения |
|
|
|
|
|
|
Содержание отчета
Отчет о лабораторной работе должен содержать:
– наименование и цель работы;
– схему лабораторной установки с указанием используемых радиоизмерительных приборов;
– заданные варианты двухполюсников;
– основные аналитические соотношения, необходимые для определения параметров двухполюсника;
– результаты измерений, сведенные в таблицу 1.1;
– результаты обработки измерений, сведенные в таблицу 1.2;
– выводы по работе.
Контрольные вопросы
1 Сформулируйте закон Ома для участка цепи.
2 Что понимается под активным сопротивлением цепи?
3 Что понимается под реактивным сопротивлением цепи?
4 Сформулируйте закон Ома в комплексной форме.
5 Что является причиной наличия сдвига фаз между напряжением и током в цепи переменного тока?
6 Записать выражение для комплексного сопротивления цепи в показательной и алгебраической формах.
7 Чему равны модуль и аргумент комплексного сопротивления цепи с последовательным соединением элементов R и L (R и C, L и C, R, L и C) ?
8 Что такое комплексная проводимость цепи? Как она соотносится с комплексным сопротивлением?
9 Чему равны модуль и аргумент комплексной проводимости цепи с параллельным соединением элементов R и L (R и C, L и C, R, L и C) ?
10 Что такое активная, реактивная, полная мощности?
11 Построить треугольник сопротивлений для различных вариантов двухполюсников.
12 Что такое действующее значение тока (напряжения)?
13 Что такое среднее значение тока (напряжения)?
14 Как связаны между собой мгновенные значения напряжения и тока в индуктивности (в емкости, в активном сопротивлении)?