
tip_1
.docx
Задача типа I
Сформулировать систему уравнений, позволяющую определить величину теплового потока через плоский слой разреженного газа. Состояние этого газа описывается четырехмоментным двухсторонним максвеллианом с параметрами n1, T1, n2, T2. Задача стационарная. Известны: температуры поверхностей TГ и ТХ, расстояние между ними L, плотность газа вблизи горячей поверхности X=0. Считается, что на горячей поверхности осуществляется полная энергетическая аккомодация, а на холодной коэффициент аккомодации, рассчитываемый по TПАД и TОТР равен 0,8.
Решение
Задача представляет собой тип I. Выбирается следующая четырехмоментная аппроксимация функции распределения:
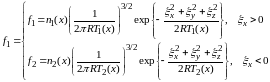
Система
уравнений сохранения массы, импульса,
энергии для принятой аппроксимация
функции распределения и произвольного
значения координаты
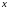 имеет вид:
имеет вид:
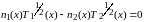
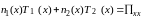 (I)
(I)
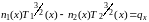
Эта
система уравнений справедлива при любом
,
т.е. и при
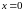 .
Следовательно,
из (I)
вытекают представленные ниже уравнения
(1) – (3):
.
Следовательно,
из (I)
вытекают представленные ниже уравнения
(1) – (3):
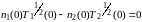 (1)
(1)
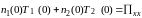 (2)
(2)
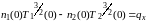 (3)
(3)
Аналогично
при
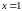 из
(I)
следует система уравнений (4) – (6):
из
(I)
следует система уравнений (4) – (6):
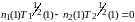 (4)
(4)
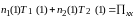 (5)
(5)
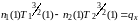 (6)
(6)
Единица для безразмерной системы, для размерной записывается через L.
Продолжение решения задачи типа I
В
шести уравнениях (1) – (6) содержатся
десять неизвестных:
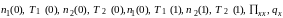 ,
т.е. для замыкания системы уравнений,
описывающей поставленную задачу, нужно
сформулировать еще четыре уравнения.
,
т.е. для замыкания системы уравнений,
описывающей поставленную задачу, нужно
сформулировать еще четыре уравнения.
По определению плотности газа как момента функции распределения и принятой аппроксимации этой функции в виде четырехмоментного двухстороннего максвеллиана получим:
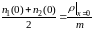
(7)
Восьмое уравнение выводится приближенно из четвертого уравнения моментной системы путем приближенного вычисления интеграла в правой его части за счет применения теоремы о среднем. Известно, что:
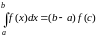 ;
;
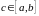 ,
если f(x)
– интегрируема (непрерывна), ограничена,
не меняет знак. Эти условия выполняются,
т.к. в данном случае f(x)
– это плотность пара, которая по своему
физическому содержанию не может быть
в данном случае разрывной, менять знак,
а значения плотности ограничены
определенными величинами. Следовательно,
применение теоремы о среднем этим
обосновано.
,
если f(x)
– интегрируема (непрерывна), ограничена,
не меняет знак. Эти условия выполняются,
т.к. в данном случае f(x)
– это плотность пара, которая по своему
физическому содержанию не может быть
в данном случае разрывной, менять знак,
а значения плотности ограничены
определенными величинами. Следовательно,
применение теоремы о среднем этим
обосновано.
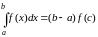 ;
;
При
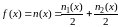 ,
,
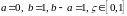 :
:
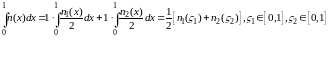
Приближенно:
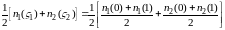
Соответственно четвертое уравнение моментной системы
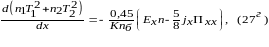
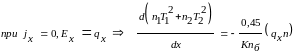
примет вид:
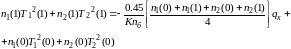 (8)
(8)
Коэффициент аккомодации энергии, рассчитываемый по TПАД и TОТР , запишется так:
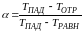 .
.
Соответственно
при
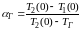 .
По условию задачи на горячей поверхности
осуществляется полная энергетическая
аккомодация, т.е.
.
По условию задачи на горячей поверхности
осуществляется полная энергетическая
аккомодация, т.е.
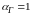 .
Следовательно:
.
Следовательно:
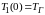 (9)
(9)
При
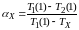 .
По
условию задачи
.
По
условию задачи
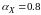 ,
откуда следует, что
по определению:
,
откуда следует, что
по определению:
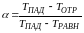
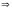
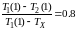 (10)
(10)
Полученная
система уравнений (1) – (10) замкнута
относительно неизвестных
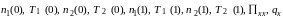 .
.
Ответ:
Сформулирована система уравнений (1) –
(10), позволяющая определить величину
теплового потока
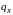 через
плоский слой разреженного газа.
через
плоский слой разреженного газа.
