3 курс / Гигиена / Физико_химические_характеристики_промышленных_альфа_излучающих_аэрозолей

В отличие от первого алгоритма, который является универсальным, второй алгоритм применим на мишенях с небольшим количеством визуализированных треков. Результаты работы первого алгоритма (рис. 5.30) и второго алгоритма (рис. 5.33) очень схожи между собой.

5.5. Моделирование поведения осколков деления 239Pu в биологическом материале

Моделирование выполнялось ИПЭ УрО РАН в рамках договора между ИПЭ УрО РАН и ФГУП ЮУрИБФ, результаты приведены далее. Данные моделирования были переданы в ЮУрИБФ в виде текстовых файлов, и на их основе были получены формулы вычисления координаты наночастицы в толстом слое. Производилось моделирование облучением тепловыми нейтронами пробы биологического материала, содержащие изотопы плутония, закладываемые в контакте с трековым детектором из особо чистого кварца, не содержащего как активирующихся примесей, так и не содержащей примесей делящихся материалов – урана и тория. В результате облучения тепловыми нейтронами, образуются осколки деления плутония, регистрируемые трековым детектором. Ядерно-физические характеристики основных радиоизотопов плутония приведены в работе [19].

Деление атомных ядер может быть вызвано различными частицами, однако практически наиболее выгодно использовать для этой цели нейтроны. Отсутствие кулоновского сил отталкивания позволяет нейтронам со сколь угодно малой кинетической энергией приблизиться к ядру на расстояние меньше радиуса действия ядерных сил. Захват ядром нейтрона приводит к возбуждению ядра, и, если энергия возбуждения достаточна, происходит деление.

Характерной особенностью деления является то, что осколки, образующиеся в результате деления, как правило, имеют существенно разные массы. Так, например, в случае наиболее вероятного деления 235U отношение масс осколков равно 1,46. Тяжелый осколок при этом имеет массовое число 139, легкий – 95. Деление на два осколка с такими массами не является единственно возможным [20]. Массовое распределение осколков деления тяжелых ядер представляет собой т. н. «двугорбую кривую». На рисунке 5.34 показаны массовые распределения осколков деления тепловыми нейтронами 234U и более тяжелых ядер, в том числе 239Pu. Вероятность деления на два равных по массе осколка не равна нулю. При делении тепловыми нейтронами вероятность симметричного деления примерно на три порядка меньше, чем в случае наиболее вероятного деления на осколки с A = 139 и 95. Асимметричное деление можно объяснить влиянием оболочечной структуры ядра. Ядро стремится разделиться таким образом, чтобы основная часть нуклонов осколка образовала устойчивый магический остов. В процессе

270

деления основная часть энергии освобождается в виде кинетической энергии осколков деления. Такой вывод можно сделать из того, что кулоновская энергия двух соприкасающихся осколков приблизительно равна энергии деления. Под действием электрических сил отталкивания кулоновская энергия осколков переходит в кинетическую энергию.

Рисунок 5.34 – Массовые распределения осколков деления тепловыми нейтронами 233U, 235U, 239Pu и спонтанного деления 252Cf, 256Fm [20]

Между кинетическими энергиями E осколков и их массами M существует следующее соотношение, вытекающее из закона сохранения импульса:

Ел/Ет = Мт/Mл (5.84)

где Ел и Mл и относятся к легкому осколку, а Ет и Мт – к тяжелому.

Кинетическая энергия осколков деления сравнительно мало зависит от энергии возбуждения делящегося ядра, так как излишняя энергия обычно идет на возбуждение внутреннего состояния осколков. Средняя масса легкой группы практически линейно растет с ростом массы делящегося ядра, в то время как средняя масса тяжелой группы остается практически неизменной (A140). Таким образом, практически все добавочные нуклоны идут в легкие осколки (рис. 5.35).

Задача моделирования – определение эффективности регистрации осколков деления для реальных условий эксперимента с учетом толщины проб биологического материала (среза) и реального энергетического распределения осколков деления. Для корректной оценки размеров частиц необходимо знать вероятность образования трека при делении плутония в облученном образце. Вероятность регистрации трека определяется различ-

271

Рекомендовано к покупке и изучению сайтом МедУнивер - https://meduniver.com/

ными параметрами, такими, как энергия осколка деления, угол вхождения в материал детектора, глубина залегания исходного ядра в облучаемом материале. Простое аналитическое решение данной задачи отсутствует. В связи с этим необходимо моделирование процессов взаимодействия осколков деления с материалом детектора для различных условий эксперимента, учитывая влияние толщины пробы биологического материала и параметры регистрирующего детектора.

Рисунок 5.35 – Зависимость средних масс легкой и тяжелой групп осколков от массы делящегося ядра [20]

Для моделирования взаимодействия ядер отдачи, образовавшихся при распаде 239Pu с веществом детектора, был использован программный пакет SRIM 2013 (TheStoppingandRange of Ions in Matter). SRIM – программный пакет, позволяющий рассчитать параметры взаимодействие ионов с материалом мишени с помощью метода Монте-Карло. В общем виде для расчетов в каждой из программ пакета необходимо задать атомный номер иона, его массу и энергию. Основной программой, входящей в пакет SRIM, используемой в данной работе является программа TRIM (TRansport of Ions in Matter). TRIM позволяет рассмотреть взаимодействие ядер отдачи со сложными мишенями, состоящих из разных материалов. Вычисления производятся на основе метода Монте-Карло (метода статистических испытаний).

Результатом моделирования в данной программе являются выходные файлы, в которых указываются энергия, направление вылета, координаты конечной точки. Также пользователь может наблюдать в реальном времени процесс моделирования на графиках столкновений в разных проекциях. Также в данной работе используется программа Ion Stopping and Range in Targets, помощью которой подсчитываются потери энергии ионов в веществе. Данная программа производит быстрые вычисления, результатом которых

272

являются таблицы тормозных способностей, пробега, и их разброса для любого иона любой энергии как в любой элементарной мишени, так и для мишеней сложного состава [21].

5.5.1. Моделирование выхода осколков деления из биологической ткани

Проводилось моделирование выхода осколков деления плутония из биологической ткани с целью последующей оценки эффективности регистрации их трековыми детекторами. Диапазон толщин биологической ткани был задан в пределах от 1 до 10 мкм и взяты значения 1, 2, 4, 7, 10 мкм. Изначальное положение и траектория вылета осколков деления задавались случайным образом. Для этого были составлены входные файлы, содержащие в себе характеристики осколков деления, такие как атомный номер элемента, энергия осколка, глубина залегания в мишени (в биологической ткани), где находилась частица в начальный момент времени (его ось х координат) и угол падения осколка, задаваемый тремя направляющими косинусами относительно осей. Энергия задавалась исходя из расчетов на основе двугорбого массового распределения осколков деления 239Pu тепловыми нейтронами, рассмотренного ранее. Атомный номер элемента подбирался в соответствии с массовым числом, полученным из данного распределения. Также на основе двугорбого распределения задавалось количество историй в соответствии с вероятностью выхода того или иного осколка деления. Результаты расчетов представлены в таблице 5.7.

Таблица 5.7 – Рассчитанные параметры осколков деления на основе «двугорбого распределения»

273

Рекомендовано к покупке и изучению сайтом МедУнивер - https://meduniver.com/

Глубина залегания задавалась случайным образом при помощи генератора случайных чисел MS Excel. Направление вылета осколка задавалось с использованием сферической системы координат. Угол вылета, определяющий направление, задается тремя направляющими косинусами, зависящими от углов θ и φ, которые изображены на рисунке 5.36. Углы θ и φ рассчитывались по формулам:

Рисунок 5.36 – Сферическая система координат

Направляющие косинусы вычислялись следующим образом:

Во входных файлах, содержалась достаточная для моделирования информация о направлении, энергии и глубине залегания осколков деления. В результате моделирования были получены выходные файлы, содержащие в себе информацию об энергии осколков деления, вышедших из образца биологической ткани, и угле, под которым осколок вылетел из мишени. Примеры энергетических распределений осколков, имеющих наибольший процент выхода на деление, в зависимости от толщины мишени представлены на рисунках 5.37–5.39. С уменьшением толщины пробы биологического материала, энергетическое распределение смещается в область больших энергий.

274

сунках 5.40–5.42. Стоит отметить, что с уменьшением толщины пробы биологического материала, угловое распределение становится более равномерным, в то время как при большой толщине биологического материала доминируют углы вылета меньше 60 градусов.

Рисунок 5.40 – Угловое распределение осколков деления с А=100, толщина пробы биологического материала 10 мкм

Рисунок 5.41 – Угловое распределение осколков деления с А=100, толщина пробы биологического материала 4 мкм

Рисунок 5.42 – Угловое распределение осколков деления с А=100, толщина пробы биологического материала 1 мкм

276

Для того чтобы проанализировать совокупный вылет осколков деления из мишени и, впоследствии, оценить эффективность регистрации трековым детектором, выходные данные были сведены в один общий файл для каждой толщины биологической ткани, и разделены по направлению вылета (прямое и обратное направления). Была сохранена пропорциональность вкладов ядер с различной атомной массой, соответствующая «двугорбой кривой». Вылет в прямом и обратном направлениях – равновероятные события, соответственно и распределения по энергиям и углам должны быть идентичны, поэтому для упрощения далее рассматривается прямое направление вылета осколков.

Наблюдается зависимость энергетического и углового распределений от толщины образца биологической ткани, то есть источника. При толщине пробы 10 мкм, то есть при толстом источнике, энергетическое распределение смещается в область малых энергий, в то время как при толщине 1 мкм энергетическое распределение соответствует двугорбой кривой и имеет два выраженных максимума в районе 65 и 95 МэВ. Данные энергетические распределения представлены на рисунках 5.43–5.46.

Рисунок 5.43 – Энергетическое распределение осколков деления, толщина пробы биологического материала 1 мкм

Рисунок 5.44 – Энергетическое распределение осколков деления, толщина пробы биологического материала 2 мкм

277

Рекомендовано к покупке и изучению сайтом МедУнивер - https://meduniver.com/

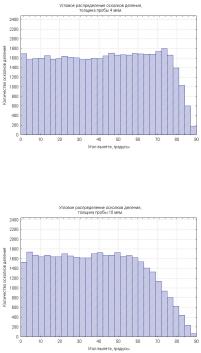
Рисунок 5.48 – Угловое распределение осколков деления, толщина пробы биологического материала 4 мкм

Рисунок 5.49 – Угловое распределение осколков деления, толщина пробы биологического материала 10 мкм

5.5.2. Моделирование взаимодействия осколков деления с материалом детектора

Для оценки эффективности регистрации осколков деления 239Pu кварцевым трековым детектором, необходимо рассчитать потери энергии при прохождении осколка деления через вещество детектора и пробег осколков деления в кварце. Полные потери энергии складываются из ионизационных потерь (электронные взаимодействия) и потерь при ядерных соударениях. Для частиц с энергией свыше 1 МэВ потери энергии за счет ядерных соударений существенно меньше, чем при взаимодействии с электронами среды [15]. Удельные ионизационные потери энергии при прохождении заряженных частиц через вещество представляют собой отношение энергии dE частицы, теряемой на ионизацию среды при прохождении отрезка dx, к длине этого отрезка. Если пролетающая через вещество частица имеет энергию большую, чем энергия связи электрона в атоме, то удельные ионизационные потери рассчитываются по формуле БетеБлоха:

279

Рекомендовано к покупке и изучению сайтом МедУнивер - https://meduniver.com/