3. Элементы электростатики
Напряженность и поток напряженности электростатического поля
Электростатика изучает свойства поля неподвижных зарядов. Основной характеристикой электростатического поля является напряженность поля. Напряженностью поля называется величина, измеряемая отношением силы, действующей со стороны поля на помещенный в данную точку пробный1 заряд, к значению этого заряда
(3.1)
Единицей измерения напряженности в СИ является В/м.
Вектор напряженности Е показывает, с какой силой действует данное поле на единичный положительный заряд, внесенный в данную точку этого поля, поэтому является силовой характеристикой поля.
Выражение для модуля напряженности поля точечного заряда и равномерно заряженной по поверхности сферы имеет вид:
(3.2)
где q
- заряд,
создающий поле, r
- расстояние
от выбранной точки до этого заряда
(или до центра сферы), 1/
нм2/кл2,
0
– электрическая постоянная СИ, равная
8,85*10-12
кл2/нм2;
- относительная диэлектрическая
проницаемость среды (для вакуума =1).
Электрическое поле принято изображать силовыми линиями (или линиями напряженности).
Силовой линией называется линия, касательная к которой в каждой точке совпадает с направлением вектора напряженности в этой точке.
Число силовых линий, пронизывающих воображаемую единичную площадку, перпендикулярную этим линиям, выбирается равным (или пропорциональным) модулю напряженности в данной точке.
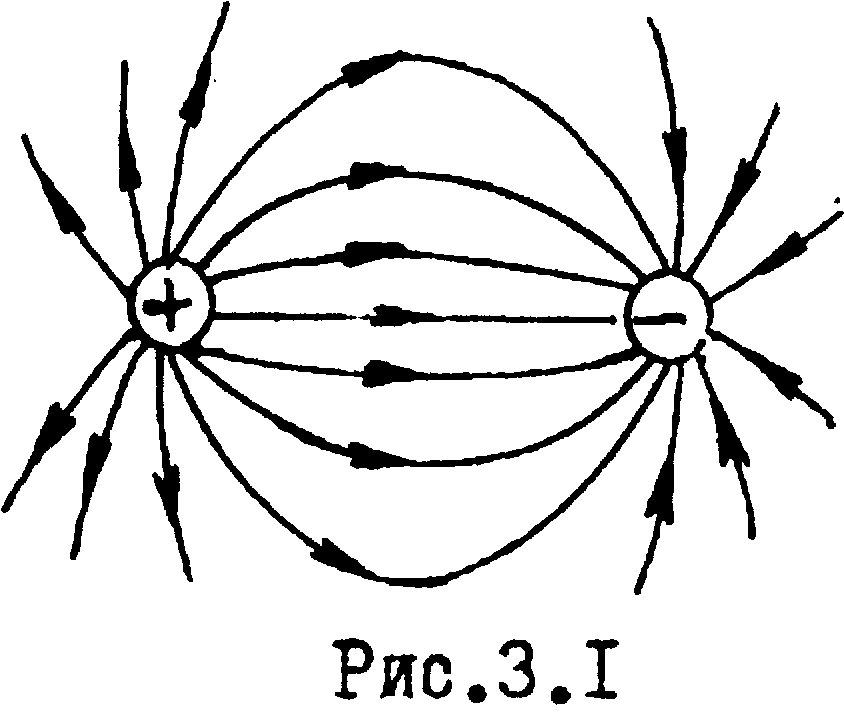
Линии напряженности электростатического поля начинаются на положительных и заканчиваются на отрицательных зарядах, нигде не пересекаясь. На рис.3.1 показана картина силовых линий двух точечных разноименных одинаковых по модулю зарядов.
Поле, вектор напряженности которого во всех точках является одинаковым (Е = const), называется однородным (рис.3.2).
Элементарным
потоком вектора напряженности Е_
через площадку ds.
находящуюся
в электрическом поле называется скалярное
произведение вектора напряженности
и вектора площадки
1:
(3.3)
Поток вектора напряженности через поверхность S равен:
(3.4)
Теорема
Гаусса
утверждает, что поток вектора напряженности
электрического поля через замкнутую
поверхность равен алгебраической сумме
заключенных внутри этой поверхности
зарядов деленной на 0:
(3.5)
Пользуясь теоремой Гаусса можно рассчитать напряженность вблизи бесконечной равномерно заряженной плоскости, поверхностная плотность заряда на которой во всех точках плоскости одинакова и равна . Пусть плоскость заряжена положительно. Для использования теоремы Гаусса выберем замкнутую поверхность вблизи плоскости в виде замкнутого цилиндра (рис.3.3), расположенного таким образом, чтобы по (3.3) можно было легко подсчитать поток вектора напряженности через его торцы S
(поток E через боковую поверхность цилиндра в соответствии с (3.3) равен нулю):
(3.6)
С другой стороны, тот же поток по (3.5) равен:
(3.7)
Сравнивая (3.6) и (3.7), получим:
(3.8)
Потенциал электростатического поля
Потенциалом данной точки поля называется величина, измеряемая отношением работы, затраченной на перемещение пробного заряда из данной точки поля в бесконечность1, к значению этого заряда:
(3.9)
Потенциал показывает, какую работу совершают силы поля при перемещении единичного положительного заряда из данной точки в бесконечность. Одновременно, потенциал точки поля характеризует запас потенциальной энергии, которой обладал единичный положительный заряд, помещенный в эту точку поля. Поэтому потенциал является энергетической характеристикой поля. Потенциал поля точечного заряда и равномерно заряженной поверхности сферы выражается формулой:
,
(3.10)
где буквенные обозначения те же, что и в (3.2).
Знак потенциала определяется знаком заряда, создающего поле.
За единицу измерения потенциала принят вольт (В).
Точки пространства, в которых потенциал имеет одно и то же значение, образуют поверхность, называемую эквипотенциальной: силовые линии перпендикулярны к эквипотенциальным поверхностям (рис.3.4).
Между напряженностью и потенциалом существует определенная связь:
проекция вектора Е на произвольное направление l равна производной от потенциала по l, т.е. скорости изменения потенциала при перемещении вдоль направления l:
;
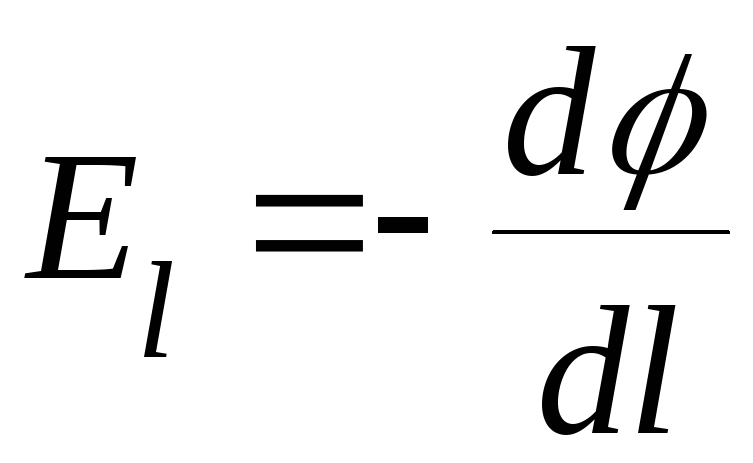(3.11)
Знак "-" показывает, что вектор Е направлен в сторону убывания потенциала. В более общем виде эта связь выражается соотношением:
(3.12)
т.е. вектор напряженности равен градиенту потенциала с обратным знаком. Для однородного поля выражение (3.11) приобретает простой вид:
(3.13)