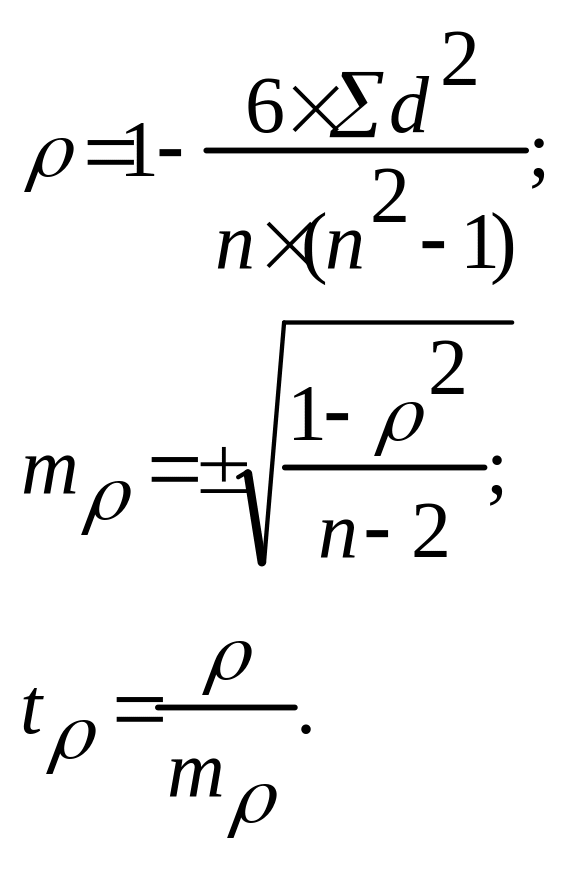Методика вычисления коэффициента ранговой корреляции

Последовательность расчета коэффициента ранговой корреляции отражена в табл. 10 и правилах, перечисленных после алгоритма.

Таблица 10

Алгоритм расчета коэффициента ранговой корреляции (р), его ошибки (m_p) и коэффициента достоверности (t_p)

Признак x	Признак y	Порядковые номера (ранги) для рядов		Разность между рангами (d=x′–y′)	Квадрат разности (d2)	Формулы для расчета
		х′	y′
1	2	3	4	5	6	7
					∑d2

1. Составить ряды из парных признаков (графы 1 и 2).

2. Каждую величину признака заменить ранговым (порядковым) номером – х′ и у′. (в тех случаях, когда имеется несколько одинаковых по величине чисел, порядковый номер обозначают средним числом из суммы очередных порядковых их номеров). Ранжировать значения обоих рядов в строго определенном направлении от меньшей величины к большей или от большей к меньшей (графы 3 и 4).

3. Определить разность между рангами для каждой пары членов ряда (по каждой строке) – графа 5.

4. Возвести в квадрат каждое из полученных значений разности между рангами и определить сумму квадратов разности рангов (d²) – графа 6.

5. Подставить полученные данные в формулу и рассчитать коэффициент корреляции рангов – графа 7.

6. Подставить необходимые данные в формулу и рассчитать среднюю ошибку (m_p) коэффициента ранговой корреляции – графа 7.

7. Подставить необходимые данные в формулу и рассчитать коэффициент достоверности (t_p) – графа 7.

Методику расчета и оценки коэффициента корреляции рангов разберем на следующем примере (см. табл. 11).

Таблица 11

Данные о заболеваемости дифтерией жителей городов

Н-ской области и о выполнении плана профилактических прививок в отчетном году

Города	Заболеваемость дифтерией (на 100 чел.)	Выполнение плана профпрививок (в %)	Ранги		Разность рангов	Квадрат разности рангов
	х	у	Х1	У1	d (х-у)	d2
А	3,29	86	1	8	7	49
Б	3,21	82	2	10	8	64
В	3,17	88	3	7	4	16
Г	2,85	84	4	9	5	25
Д	2,84	90	5	6	1	1
Е	2,71	95	6	4	2	4
Ж	2,23	100	7	1	6	36
З	1,82	92	8	5	3	9
И	1,80	98	9	2	7	49
К	0,70	96	10	3	7	49
						∑d2=302

Подставим полученные данные в формулу и рассчитываем коэффициент ранговой корреляции:

Рассчитаем среднюю ошибку (m_p):

Рассчитаем коэффициент достоверности:

Условием достоверности коэффициента корреляции рангов, как, впрочем, и всех остальных коэффициентов корреляционной зависимости, является превышение коэффициента своей утроенной ошибки:

Таким образом, –0,833×0,197 или –0,83>0,591 т.е. полученные результаты достоверны.

Вывод. Полученный коэффициент корреляции рангов статистически достоверен. Следовательно, можно говорить о сильной, обратной связи между заболеваемостью дифтерией и процентом выполнения плана профилактических прививок. Заболеваемость выше в тех городах, где план профилактических прививок выполнен недостаточно.

При вычислении коэффициента корреляции по методу рангов бывают случаи, когда отдельные показатели ряда встречаются несколько раз. В этом случае порядковый номер каждого из них (ранг) определяется как средняя из сумм очередных порядковых номеров. Например, надо поставить порядковые номера (ранги) показателей возраста 10 студентов:

Возраст (годы), Х

22

22

21

24

23

23

24

23

24

24

Ранги по величине показателей возраста проставляются следующим образом: возраст 21 год, его порядковый номер = 1. возраст 22 года встречается дважды, занимая по своей величине 2-е и 3-е места, поэтому порядковые номера в данном случае будут равны полусумме занимаемых этим возрастом мест – (2+3):2=2,5, т.е. против каждого показателя возраста 22 года будет поставлен порядковый номер (ранг) 2,5. возраст 23 года встречается 3 раза, занимая 4-е, 5-е и 6-е места соответственно, т.к. 2-е и 3-е места использованы для возраста 22 года. Ранги для возраста 23 года будут равны – (4+5+6):3=5, т.е. против каждого возраста 23 года необходимо поставить порядковый номер (ранг) 5. в целом ранги показателей возраста у студентов будут следующие:

Возраст (годы), Х	22	22	21	24	23	23	24	23	24	24
Ранги	2,5	2,5	1	7,5	5	5	7,5	5	7,5	7,5

МЕТОДИКА ВЫЧИСЛЕНИЯ

КОЭФФИЦИЕНТА АССОЦИАЦИИ

Последовательность расчета коэффициента ассоциации отражена ниже.

Алгоритм расчета коэффициента ассоциации (Q),

его ошибки (m_a) и коэффициента достоверности (t_a).

1. Построить четырехпольную таблицу. В первом столбце этой таблицы наносят обе разновидности одного явления – Х₁ и Х₂, а в первой строке – обе разновидности второго – У₁ и У₂.При этом Х₁ и У₂ обозначают положительные разновидности (например, выздоровевшие, иммунизированные и т. д.), а Х₂ и У₂ – отрицательные (например, не выздоровевшие, не иммунизированные). Обозначить через буквы а, в, с, d четыре поля, в которые внести исходные данные:

Y Х	Y1 Заболело	Y2 Не заболело
Х1 Вакцинировано	а	в
Х2 Невакцинировано	с	d

2. Вычислить произведения аd и вс.

3. Подставить полученные данные в формулу и рассчитать коэффициент ассоциации.

4. П одставить необходимые данные в формулу и рассчитать среднюю ошибку коэффициента ассоциации.

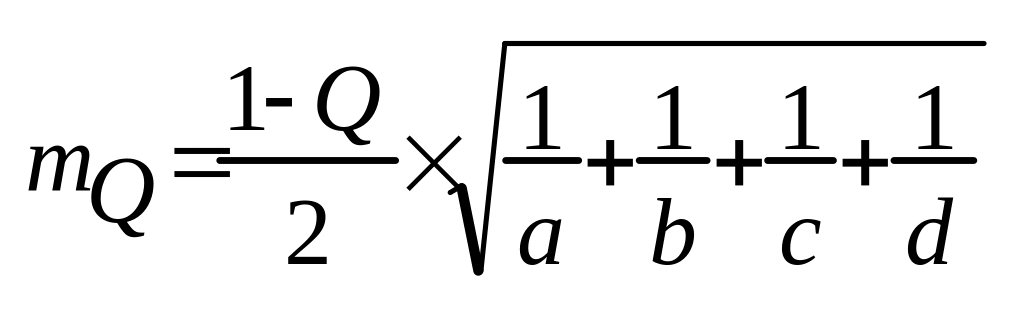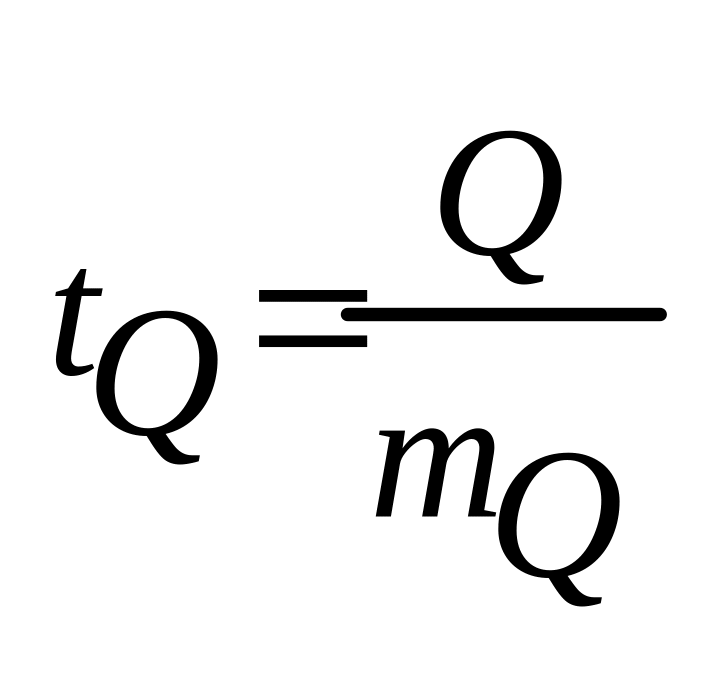5. Подставить необходимые данные в формулу и рассчитать коэффициент достоверности.

Методику расчета и оценки коэффициента ассоциации разберем на следующем примере.

Необходимо определить, влияет ли вакцинация против гриппа на заболеваемость от этой инфекции. Известно, что на промышленном предприятии с общей численностью в 2000 человек 1200 рабочим были сделаны прививки против гриппа, а 800 рабочих остались не привитыми. Заболело из привитых 240 человек, а из непривитых – 320.

Данные о заболевших и не заболевших среди привитых и не привитых приведены в табл. 12.

Таблица 12

Распределение заболевших и не заболевших среди

привитых на промышленном предприятии

	Заболело	Не заболело	Всего
Привитых	240	960	1200
Не привитых	320	480	800
Всего	560	1440	2000

Вычислим произведения аd и вс:

a×d=240×480=11520

b×c=960×320=307200

Подставим полученные данные в формулу и рассчитаем коэффициент ассоциации:

Рассчитаем среднюю ошибку (m_Q):

Рассчитаем коэффициент достоверности:

Таким образом, –0,453×0,0740,222. Коэффициент статистически достоверен, что означает, что существует обратная, средней силы связи между заболеваемостью гриппом и вакцинацией против него.