
- •Введение
- •Рекомендации по решению задач
- •Требования к оформлению
- •Критерии и шкала оценивания устной защиты решения задач
- •1. Кинематика поступательного и вращательного движения формулы
- •Примеры решения задач
- •2. Динамика поступательного движения формулы
- •Примеры решения задач
- •3. Закон сохранения импульса тела. Столкновения частиц формулы
- •Примеры решения задач
- •4. Закон сохранения энергии формулы
- •Примеры решения задач
- •5. Динамика вращательного движения формулы
- •Примеры решения задач
- •6. Гармонические колебания формулы.
- •Примеры решения задач
- •7. Уравнение состояния идеального газа формулы
- •Примеры решения задач
- •8. Первое начало термодинамики формулы
- •Примеры решения задач
6. Гармонические колебания формулы.
Дифференциальное уравнение гармонических колебаний:
 ;
;
здесь m – масса точки, k – коэффициент квазиупругой силы (k = mω02);
Уравнение механических гармонических колебаний:
 ,
,
здесь x – смещение от положения равновесия или значение колеблющейся величины, xmax – амплитуда колебаний, ω0 – циклическая собственная частота, t – время, φ0 – начальная фаза, (ω0t + φ0) – фаза колебаний;
Период колебаний:
,
здесь N – число колебаний за время t;
Частота колебаний:
 ;
;
Циклическая частота:
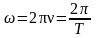 ,
,
Скорость и ускорение гармонических колебаний, соответственно:
 ,
,
 ;
;
Собственная частота и период колебаний математического маятника:
 ,
,
 ,
,
здесь g – ускорение свободного падения, ℓ – длина подвеса;
Собственная частота и период колебаний пружинного маятника:
 ,
,
 ,
,
здесь k – жёсткость пружины, m – масса тела, прикреплённого к пружине;
Период крутильных колебаний на упругой нити:
 ,
,
здесь I – момент инерции тела относительно оси, совпадающей с упругой нитью, k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается;
Сила, возвращающая тело в положение равновесия в пружинном маятнике:
Fвозвр = kx,
здесь k = mω02;
Кинетическая энергия, потенциальная энергия, полная энергия пружинного маятника, соответственно:
 ,
,
 ,
,
 ;
;
Уравнение волны:
 ,
,
здесь ℓ – расстояние вдоль луча от источника волны до некоторой точки, t – время, xmax – амплитуда колебаний, ω – циклическая частота, λ – длина волны, k – волновое число;
Скорость распространения волны:
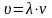 ,
,
здесь ν – частота волны,
Скорость распространения электромагнитной волны:
 ,
,
здесь n – показатель преломления волны в некоторой среде, c = 2,99792458∙108 м/с – скорость света в вакууме;
Разность фаз:
 ;
;
Дифференциальное уравнение затухающих колебаний:
 ,
,
здесь m – масса точки, r – коэффициент сопротивления, β – коэффициент затухания, β = r/(2m);
Уравнение механических затухающих колебаний:
 ,
,
здесь
A0
– начальная амплитуда, ω – частота
затухающих колебаний
 ;
;
Время релаксации, логарифмический декремент затухания и добротность, соответственно:
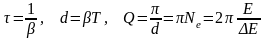 ,
,
здесь Ne – число колебаний, в течении которых амплитуда колебаний уменьшается в «e», E – среднее значение запасенной энергии в системе за некоторый промежуток времени, равный одному периоду колебаний, ΔE –потери энергии системе за тот же промежуток времени;
Дифференциальное уравнение вынужденных колебаний:
 ,
,
здесь F0cos(ωt) – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания, F0 – ее амплитудное значение, f0 = F0/m;
Амплитуда вынужденных колебаний:
 ,
,
Резонансная частота и резонансная амплитуда, соответственно:
 .
.
Оглавление
Примеры решения задач
1. Длина маятника, демонстрирующего вращение Земли в Исаакиевском соборе в Ленинграде, равна 98 м. Определите период его свободных колебаний.
Дано: ℓ = 98 м; g = 9,8 м/с2; |
Решение: Так как амплитуда колебаний маятника и размеры тела на подвесе малы по сравнению с длиной подвеса, его колебания можно считать гармоническими и для описания колебаний применить формулу периода колебаний математического маятника:
|
T – ? |
Ответ: T = 20 с.
2. При подвешивании груза массой 1 кг стальная пружина в положении равновесия удлинилась на 1 см. С каким периодом будет совершать колебания этот груз на пружине после смещения его по вертикали из положения равновесия?
Дано: m = 1 кг; x = 1 см; g = 9,8 м/с2; |
Решение: Под действием силы упругости пружины тело массой m совершает гармонические колебания с периодом, определяемым по формуле , |
T – ? |
где k – жесткость пружины.
Жесткость пружины можно найти по ее удлинению под действием силы тяжести груза массой m. По закону Гука
 .
.
Для модуля силы упругости в положении равновесия выполняется равенство
 ,
,
следовательно,
 .
.
Подставляем полученное выражение в формулу для вычисления периода колебаний:
 .
.
Мы получили, что для решения задачи достаточно было знать только удлинение пружины в положении равновесия, так как масса тела не входит в окончательную расчетную формулу.
Ответ: T = 0,2 с.
Оглавление

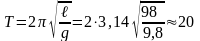 с.
с.