
- •Напряженность электростатического поля
- •Принцип суперпозиции полей
- •Г рафическое изображение электрических полей. Силовые линии
- •Поле равномерно заряженной бесконечной плоскости
- •Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)
- •Поле равномерно заряженной сферической поверхности
- •Переходные процессы в конденсаторах (разрядка конденсатора).
- •1. Проводники и диэлектрики
- •2. Заряженный проводник
- •3.Проводники во внешнем электр. Поле
- •3.Движение заряженных частиц в магнитном поле.
- •2. Заряженная частица движется перпендикулярно линиям магнитной индукции
- •3. Скорость заряженной частицы направлена под углом к вектору.
1. Проводники и диэлектрики
Проводники-вещ-ва в которых есть свободные электрические заряды. Концентрация в проводниках такая же, чтоб и концентрация атомов. Эти заряды могут перемещаться в пределах проводника, если в нём создано электрическое поле
Диэлектрики- вещ-ва, в которых почти нет свободных электрических зарядов. В модели идеального диэлектрика свободные заряды отсутствуют
Полупроводник- по концетрации свободных зарядов занимают промежуточное положение положение между проводниками и диэлектриками. У них концентрация очень зависит от температуры
2. Заряженный проводник
Если проводник заряжен, то свободные заряды в нём придут в движение и двигаться они будут до тех пор, пока напряжённость электрического поля не станет равной 0
𝐹=𝑞𝐸
𝐸𝑥=𝜕𝜑𝜕𝑥 𝐸𝑦=𝜕𝜑𝜕𝑦
𝐸𝑧=𝜕𝜑𝜕𝑧
E=0
𝐸𝑥=𝐸𝑦= 𝐸𝑧=0
𝜕𝜑𝜕𝑥 =𝜕𝜑𝜕𝑦=𝜕𝜑𝜕𝑧=0=𝑐𝑜𝑛𝑠𝑡
Следовательно внутри заряженного проводника потенциал постоянен, тоесть объём проводника и его поверхность эквипотенциальны
Если Е равняется 0, значит равен 0 поток вектора напряж. электр. поля черех любую замкнутую поверхность внутри проводника
Согласно т. Гаусса, следует, что объёмная плотность заряда внутри проводника=0
Ф=∫𝐸𝑛𝑑𝑠=0𝑆
𝜌=𝜕𝑞𝜕𝑣=0 q=const
Возьмём на поверхности проводника небольшой участок dS и построим на нём Гауссов ящик, как это делается при расчёте поля вблизи равномерно заряж. плоскости
Ф𝐸=𝜎∆𝑠𝜀𝜀0
Для уединённого проводника при заданном его потенциале поверхностная плотность заряда определяется кривизной его поверхности
3.Проводники во внешнем электр. Поле
Если внести проводник в область, где существует электр. поле, то в а начальный момент времени поле в проводнике существует от действия силы на заряды в электр. поле свободные заряды придут в движение и будут перемещаться, пока напряж. электр. поля не станет равной 0. В результате движение зарядов в противоположных концах проводника возникают поверхностные заряды противоположного знака -
𝐸0+a |𝐸|=|𝐸0|
Электроны под действием F начинают двигаться против поля
Перераспределённые заряды создают поле Е0 направленное на встречу Еполн
2.Проводник с током в магнитном поле. Взаимодействие параллельных токов. Движение заряженных частиц в магнитном поле
Рис.
10
 ,
действующая на элемент длины проводника
с током в неоднородном магнитном поле
(рис. 10) ,
,
действующая на элемент длины проводника
с током в неоднородном магнитном поле
(рис. 10) ,
 (34)
(34)
dF
= Id Вsin
Вsin .
(35)
.
(35)
Формулы (34), (35) называют законом Ампера.
Интегрируя эти выражения по элементам тока, находим силу Ампера, действующую на линейный или объемный участок проводника с током (при условии, что ток течет по тонкому проводнику,
jdV = Id ),
Рис.
11
 .(36)
.(36)
Направление силы Ампера можно найти по правилу правого винта (рис. 11). В однородном магнитном поле сила Ампера
F = I Bsin, (37)
где
угол между проводником и
 .
.
Взаимодействие параллельных токов
Найдем силу взаимодействия двух параллельных проводников с током бесконечной длины в вакууме ( = 1, рис. 12).
Рис.
12
Индукция магнитного поля проводника с током I1
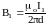 б(38)
б(38)
По закону Ампера на проводник с током I2 действует сила
 .
(39)
.
(39)
На основании третьего закона Ньютона
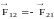 (рис.
12).
(рис.
12).
С учетом (38) формулу (39) перепишем в виде
 (40)
(40)
Так как проводники бесконечной длины, найдем силу, действующую на единицу длины проводника, в виде
 .(41)
.(41)
Если ток течет по проводам в противоположных направлениях, то они отталкиваются друг от друга.
