Билет 1

1.Закон сохранения заряда. Закон Кулона. Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется. Зако́н Куло́на — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами.

2.Уравнение непрерывности. Закон Ома для однородного участка проводника.

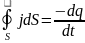–ур-ние непрерывности j- Поток вектора через фигуру S. q- суммарный электрический заряд изменяется за время dt.

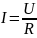– закон ома для однородного участка цепи.

Билет 2

1. Электрическое поле. Напряжённость электрического поля. Принцип суперпозиции электрических полей. Графическое изображение электрических полей

Взаимодействия зарядов передаются с помощью особого материального посредника, называемогоэлектрическим полем. Взаимодействие двух зарядов q₁ и q₂ можно объяснить так: в пространстве вокруг заряда q₁ существует особая форма материи – электрическое поле, которое и действует непосредственно на заряд q₂.

Напряженность электростатического поля

Напряженность поля  - векторная ха­рак­те­ристика электрического поля. Напря­жен­ность поля в некоторой точке определяется отно­шением силы , действующей со стороны поля на положительный зарядq₀, помещенный в данную точку поля, к величине этого заряда:

, .

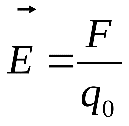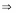
Принцип суперпозиции полей

Напряженность поля, создаваемая в какой-либо точке пространства системой зарядов, равна векторной сумме напряженностей, создаваемых в этой точке каждым из зарядов:

,

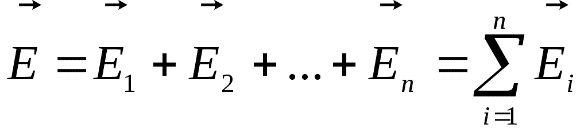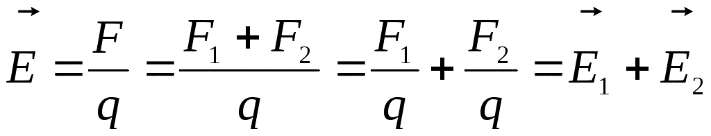
Напряженность поля непрерывно распределенного заряда:   . (4)

Характеристики распределенных зарядов

- линейная плотность зарядов;

- поверхностная плотность зарядов;

- объемная плотность зарядов;

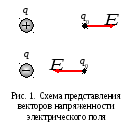
Г рафическое изображение электрических полей. Силовые линии

С иловые линии – это непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности электрического поля.

Свойства силовых линий

• силовые линии всегда начинаются на положительных зарядах и заканчиваются на отрицательных;

• силовые линии начинаются и заканчиваются либо на зарядах, либо уходят в бесконечность;

• густота силовых линий (число силовых линий, проходящих через единицу площади) пропор­ци­о­нальна напряженности электрического поля;

• силовые линии не пересекаются.

2.Сторонние силы. Закон Ома для неоднородного участка цепи.

Д ля того, чтобы поддерживать ток в цепи, нужно от конца проводника с мень­шим потенциалом непрерывно отводить приносимые током заряды, а к концу с большим потенциалом непрерывно их подводить. В замкну­той цепи наряду с участками, на которых положительные носители движутся в сто­рону убывания потенциала, должны иметься участки, на которых перенос положи­тельного заряда происходит в направлении возрастания потенциала, т.е. против сил электро­статического поля. Перемещение носителей на этих участках возможно лишь с по­мощью сил не электростатического происхождения, называемых сторон­ними сила­ми.

Закон Ома для неоднородного участка цепи имеет вид:

R-общее сопротивление неоднородного участка.

Билет 3

1. Поток вектора напряжённости электрического поля. Теорема Гаусса

Поток вектора напряженности электрического поля.

Допустим что в каждой точке пространства определено значение напряжения эл.поля. Выберем в пространстве dS площадка должна быть на столько малой чтобы в пред ее вектор Е можно было считать постоянной, ориентация площадки определяется вектором ед.нормали

При
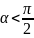
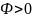
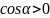
При

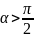
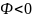
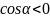
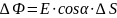
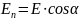
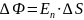
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔS_i, определить элементарные потоки  поля  через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора  через замкнутую поверхность S 

.

Теорема гаусса в интегральной форме

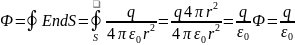
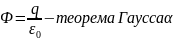
Если заряд находиться вне замкнутой поверхности то, поток Е создаваемый этим зарядом равен нулю,т.к каждая силовая линия дважды пересекает поверхность. С «-» когда входит в объём и с «+» когда выходит из него.

Теорема Гауса-поток в-ра. Е эл.поля через любую замкнутую поверхность равен алгибраической сумме зарядов находящихся внутри поверхности, делённой на эл. Постоянную.

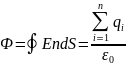
2. Работа, мощность, КПД источника тока. Тепловое действие тока. Закон Джоуля-Ленца

Рассмотрим однородный участок 1-2 проводника, к которому приложена разность потенциалов ₂ - ₁. Если по проводнику течет ток I, то за время dt через поперечное сечение его будет перенесен заряд dq = Idt.

Следовательно, силы поля совершат элементарную работу

A = dq(₂- ₁) = I(₂ - ₁)dt = IUdt.

Полезная работа на всем участке 1- 2

А= Iut = I²Rt.

Если электрическая цепь замкнута и содержит источника с ЭДС 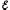, то вся затраченная источником тока работа А_З = А_П + А_ВНУТ,

где А_З = I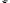 t, А_П = IU_Rt, А_ВНУТ = IU_rt.

Тогда = U_R + U_r = IR+ Ir

где U_R - напряжение на внешнем сопротивлении, U_r - напряжение на внутреннем сопротивлении источника тока.

Мощность тока можно найти по формуле N = .

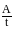Развиваемая источником тока затраченная мощность

N_З = N_П + N_ВНУТ

где N_З= I , N_П = IU_R, N_ВНУТ = IU_r.

КПД источника тока можно найти по формуле

 = .

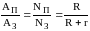Затраченная источником тока мощность

N_З = I = /(R+r),

где I = /(R + r).

Полезная мощность, выделяемая во внешнем участке цепи

N_П = IU_R = I²R = .

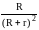
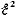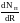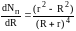
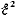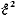Следовательно, затраченная и полезная мощности являются функциями от внешнего сопротивления. Если R 0, то N_П  0; R , то N_П  0. В этом случае функция N_П = f₂ (R) имеет один максимум. Найдем условие, при котором полезная мощность максимальна, т. е. N_П = N_П, _МАХ. Для этого производную приравняем нулю, т. е. = 0, т. е. (r²-R²) = 0. (  0, то R = r и  = 0,5). Вывод: Если R = r , то полезная мощность максимальна, а КПД источника тока равно 50%.

Тепловое действие тока. Закон Джоуля-Ленца.

При прохождении тока по проводнику происходит его нагревание, т. е. выделяется некоторое количество теплоты Q.

Для определения выделяющегося количества теплоты за единицу времени рассмотрим однородный участок проводника, к которому приложена разность потенциалов ₁  ₂.

На основании закона сохранения энергии эта работа переходит во внутреннюю (тепловую) энергию, в результате чего проводник нагревается.

Так как при прохождении тока в металлических проводниках не происходит изменение внутренней структуры металла, то вся работа сторонних сил идет на выделение тепла, т. е. А = Q.

Q = IUdt = I²Rdt.

Если на участке цепи выделить некоторый объем dV, то формула примет вид

Q = j²dVdt.

Если в последнем выражении левую и правую части разделить на dVdt,

то получим удельную тепловую мощность:

Q_уд = j²,

т. е. удельная тепловая мощность определяет количество теплоты, которое выделяется в единице объема проводника за единицу времени, и численно равна произведению удельного сопротивления проводника на квадрат плотности тока.

Если на заряды проводника действуют только электрические силы, то на основании закона Ома имеем

Q_уд = Е²

Если участок цепи неоднородный, то выделяемое количество теплоты по закону сохранения энергии будет равно алгебраической сумме работ кулоновских и сторонних сил.

Умножив правую и левую части формулы на силу тока I получим

I²R = (₁  ₂)I + ₁₂I

Следовательно, из уравнения следует, что тепловая мощность

Q = I²R ,

выделяемая на участке цепи 1-2, равна алгебраической сумме мощностей кулоновских и сторонних сил. Если цепь замкнута, то затраченная мощность

N =I  .

Билет 4

1. Применение теоремы Гаусса для расчёта электрических полей. Типы распределения заряда. Поле бесконечной равномерно заряженной плоскости

Использование теоремы Гаусса для расчета полей эффективно в тех случаях, когда поле обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической). Симметрия и конфигурация поля должны быть такими, чтобы, во-первых, заряженное тело можно было бы окружить достаточно простой замкнутой поверхностью и, во-вторых, вычисление потока вектора напряженности свести к простому умножению Е (или E_n) на площадь поверхностиSили часть ее. Если этого сделать нельзя, то задачу необходимо решать другими методами.