
- •Примеры основных процедур, которые используются в лабораторных работах
- •CommandButton 1.Caption = «Команда1»
- •If I=0 Then
- •For I=0 To 100 Step 10
- •Пример 7. Остановить выполнение программы
- •Последовательность выполнения лабораторной работы
- •Какое-то из окон во время работы может оказаться невидимым. Чтобы оно появилось, в меню основного окна надо выбрать:
- •Label1.Caption = «Привет!!!»
- •If I=0 Then
- •For I=0 To 100 Step 10
- •Button
- •OptionButton
- •Current
- •Right
- •DrawMode
- •DrawStyle
- •DrawWidth
- •VScrollBar
- •HscrollBar
- •Изображение
- •OptionButton
- •VScrollBar
- •Right
- •DrawMode
- •HScrollBar
- •DrawStyle
- •Изображение
- •Current
- •DrawWidth
- •Button
18
Лабораторная работа № 1:
"Составление простейшей программы на языке Visual Basic с рисованием основных геометрических фигур"
Основные понятия, используемые в лабораторной работе: Форма. Система координат формы. Объект. Свойство. Метод. Этапы составления программы. Процедуры. Проект. Рисование точки, линии, прямоугольника, круга, эллипса вручную и программно.
Введение
Цель первой лабораторной работы - "освоить" пространство Visual Basic, поэтому просто реализуем всё, что перечислено в разделе " Основные понятия, используемые в лабораторной работе ".
Основные операторы
'Нарисовать точку с координатами X=10,Y=20. PSet (10, 20), RGB(0, 0, 0)
'Нарисовать линию между точками X1=20,Y1=30 и X2=100,Y2=200 Line (20, 30)-(100, 200), RGB(0, 0, 0)
'Нарисовать прямоугольник, у которого координаты противоположных углов X1=150,Y1=30 X2=200,Y2=300
Line (150, 30)-(200, 300), RGB(0, 0, 0), B
'Нарисовать окружность с радиусом R=50 и центром в точке X=340, Y=80 Circle (340, 80), 50, RGB(0, 0, 0), , , 1
'Нарисовать сектор окружности
Circle (340, 80), 50, RGB(0, 0, 0), -0.7, -2.1 'Нарисовать окружность с "выкушенным" сектором
Circle (340, 80), 50, RGB(0, 0, 0), -2.1, -0.7
'Нарисовать эллипс, вытянутый по оси X (аспект=0.4) Circle (500, 80), 50, RGB(0, 0, 0), -2.1, -0.7, 0.4
'Нарисовать эллипс, вытянутый по оси Y (аспект=4) Circle (600, 80), 50, RGB(0, 0, 0), , , 4
Пример 1. Щелчком мыши по командной кнопке CommandButton1 изменить заголовок метки “Label1” на заголовок «Привет!!!» (то есть изменить свойство Caption метки Label1)
Private Sub CommandButton1_Click()
Label1.Caption = «Привет!!!»
End Sub
Пример 2. Пример процедуры с условным оператором
19
Private Выбор_Click()
I=0
If I=0 Then
Текст1.Text=” 0 “ Else
Текст1.Text=” I не равно нулю “
End If
End Sub
Пример 3. На форме имеется линия с координатами конечных точек (5,100) и (500,100). Щелчком мыши по командной кнопке CommandButton1 нарисовать на форме 11 линий, параллельных оси X и отстоящих друг от друга на расстоянии 10 пикселов (Step(Шаг)=10)
Рисуем линию между точками с координатами X1=5,Y1=100 и X2=500,Y2=100, рисуем следующую линию между точками X1=5,Y1=110=(100+10) и X2=500,Y2=110 (100+10), и т.д. Процедура для рисования этих линий будет выглядеть следующим образом (используется оператор цикла For …. Next ):
Private Sub CommandButton1_Click()
For I = 0 To 100 Step 10 ‘ верхняя граница цикла
Line (5, 100 + I) - (500, 100 + I), RGB(0, 0, 0)
Next I 'конец (нижняя граница цикла)
End Sub
Пример 4. Нарисовать концентрические окружности с радиусами 20, 30, … , 100 и центром в точке X=100, Y=200 (использовать оператор цикла For …. Next ):
Private Sub Окружности_Click()
For I=0 To 100 Step 10
Circle (100,200), 20 + I , RGB(255,0,0), , ,1
Next I
End Sub
Лабораторные основы
Цель работы: усвоить основные этапы написания программы на языке Visual Basic; научиться использовать оператор цикла и условный оператор.
Порядок выполнения работы
1."Набросать" на форму объекты: линия, фигура, командная кнопка. Изменить их свойства
в
таблице свойств:
для формы - свойство "Caption" и цвет фона;
для линии - координаты концов, тип линии, толщину, цвет рисования; для фигуры - тип фигуры, толщину контура, цвет контура, наличие заливки;
20
для командной кнопки — имя, надпись ("Caption"), шрифт надписи. Изменения этих свойств - видимы .
Это рисование вручную .
2.Сохранить файл формы Forml.frm как JIaб1.frm, файл проекта Projectl.vbp как
JIaб1.vbp.
3.Перейти в окно кода и в процедуру CommandButton_Click() вписать по одной строчке для формы, линии, фигуры, командной кнопки, которые изменяли бы какое-либо из свойств из п.1
Объект. Свойство. Метод. Это рисование программно .
4.Сконструировать цикл For.... Next для линий или окружностей.
21
Лабораторная работа № 2:
" Работа с мышью. Графический редактор "
Математические основы
Эта лабораторная работа предполагает создание маленького графического редактора. Что обычно умеет делать простейший графический редактор? Рисовать линии разной толщины и различных цветов на фоне, цвет которого мы можем изменять по нашему выбору. Значит, мы должны научить наш редактор изменять толщину линий, переключать цвета для линий и фона и, конечно, стирать нарисованное.
Программируя действия мыши, можно «заставить» появляться и исчезать курсор мыши, рисовать или, наоборот, запрещать рисование в зависимости от того, какая клавиша мыши нажата.
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ
В этой лабораторной работе делается попытка написать свой графический редактор. С имеющимися в нашем распоряжении возможностями может получиться редактор с небольшим набором инструментов, но похожий на стандартный редактор Windows Paint.
1. Запустить графический редактор Paint. Выполнить в нем самые простые операции, например, изменить цвет фона, выбрать цвет рисования, выбрать инструмент рисования и нарисовать
несколько линий разной толщины. Это нужно для того, чтобы вспомнить приемы работы в графическом редакторе, а затем написать фрагменты программы в нашем редакторе, которые обеспечат реализацию похожих инструментов: Тонкость и Ластик. Закрыть Paint без сохранения файла.
ЧАСТЬ I. "Установка основных параметров для рисования"
1.Выбрав Цвет фона и Цвет рисования, изменив толщину рисования, нарисовать на форме несколько линий. Всегда начинать рисование со щелчка мышкой по кнопке "Разрешить/Запретить рисование мышью" !!!
2.В процедуре "Тонкость" дописать строку реализации уменьшения толщины рисования (по аналогии с процедурой "Толщина").
3.В процедуре "Ластик" вписать строку реализации ластика.
ЧАСТЬ II "Основные события мыши" Существуют 3 основных события мыши:
Событие MouseDown происходит, когда нажата одна из кнопок мыши(левая или правая).
22
Событие МоusеМоve происходит, когда перемещаем указатель мыши. Событие MouseUp происходит, когда отпускаем кнопку мыши.
Написать фрагменты программы в процедурах этих событий, чтобы на форме появлялись визуальные подтверждения этих событий (например, цепочка окружностей и т.д.). В редакторе можно комбинировать использование клавиатуры и мыши. Пример использования см. в процедуре Form_MouseMove: здесь используется клавиша SHIFT.
ЧАСТЬ III "Создание кисти"
В этой части лабораторной работы написать фрагмент программы (в процедуре Form_MouseMove), который реализует кисть. Здесь наш редактор будет похож на Adobe Photoshop. Кисть - это в общем случае инструмент, содержащий некое изображение, которое является как бы мазком кисти. Мы должны понимать, что даже очень сложное изображение - это сочетание примитивов: точек, линий, основных геометрических фигур (окружности, квадраты и т.д.). При перемещении мыши мазок кисти, а значит и созданное нами изображение многократно повторится на форме.

23
Лабораторная работа № 3:
"Простейший алгоритм построения отрезка и окружности. Алгоритм Брезенхема для построения отрезка и окружности"
Математические основы
Экран дисплея - это экран растрового дисплея. Экран - это решетка с практически невидимыми глазу отдельными ячейками. Ячейки решётки называются пикселами. Очевидно, что чем меньше ячейка ( пиксел ), тем более чётким получается изображение. Принято говорить не о размере решётки или размере пиксела, а о разрешении экрана. Разрешение экрана - это количество пикселов на экране. Например, разрешение экрана может быть 640 х 480 пикселов, 1024 х 768 пикселов и т.д.
Для того, чтобы на экране появилось какое-либо изображение, надо определённым цветом высветить определённый набор пикселов. То есть ответить на вопросы:
Где на экране высветить пиксел ( то есть где на экране поставить точку ) ? Каким цветом высветить этот пиксел?
Какие пикселы высветить, чтобы получить требуемое изображение?
Рис. 1 Построение растрового изображения на экране дисплея
Когда мы рисуем отрезок на бумаге, то это просто непрерывная линия, соединяющая две точки. Рисование отрезка на экране - это выбор на каждом шаге пиксела, который надо подсветить, чтобы в итоге цепочка посвеченных пикселов создала иллюзию линии, соединяющей конечные точки отрезка. Для вертикальных, горизонтальных и наклонённых под углом 45° отрезков выбор пикселов очевиден. Если угол наклона - другой, то требуется сформулировать правила, которые бы позволили выбирать пикселы для рисования отрезка ( или кривой, если говорить в общем случае ).

24
Рис.2 Выбор пикселов при построении отрезка на экране .
Существуют алгоритмы ( и появляются новые ) рисования отрезков. Естественно, что все эти алгоритмы - разные, но есть несколько правил, общих для всех алгоритмов:
1.Отрезки должны начинаться и заканчиваться в заданных точках.
2.Отрезки должны выглядеть прямыми .
3.Яркость вдоль отрезка должна быть постоянной, не зависеть от длины и наклона.
4.Рисовать надо быстро, чтобы глаза воспринимали отрезок как единое целое, а не как цепочку бегущих пикселов.
Простейший алгоритм построения отрезка
Рассмотрим задачу построения отрезка на растровой плоскости, соединяющего точки P(x1, y1) и Q(x2, y2). Зеркальным отображением мы всегда сможем добиться, чтобы
0 ≤ y2 − y1 ≤ x2 − x1
Это несколько упростит нашу задачу.
Существует несколько подходов, зависящих от представления отрезка. Мы можем использовать математическое задание:
y = y |
+ |
y2 |
− y1 |
(x − x ), x [x , x |
2 |
] |
|
|
|
||||||
1 |
x2 |
1 |
1 |
|
|||
|
|
− x1 |
|
|
|
||
Основные недостатки этих алгоритмов очевидны. Это использование операций с вещественными числами и слишком сложные вычисления для построения обычного отрезка.
Алгоритм Брезенхема для построения отрезка.
Каждый пиксел имеет 8 соседей N, NE, NW, W, E, SE, SW, S. Предположим, что во время построения отрезка, мы поставили некоторую точку M (x,y). Тогда следующим мы поставим либо E либо NE пиксел. Как определить, какой из двух вариантов наиболее точно будет продолжать линию? Это можно определить с помощью срединной точки (рис.1) Если отрезок проходит выше срединной точки, то следующим ставится NE пиксел, иначе, если отрезок проходит ниже срединной точки, то ставится E пиксел. Сделать это математически поможет формула отрезка в неявно заданном виде:
F (x, y) = (x − x1 )dx −( y − y1 )dy dx = x2 − x1
dy = y2 − y1
F(x,y)=0 – значит точка (x,y) лежит на отрезке F(x,y)<0 – выше отрезка
F(x,y)>0 – ниже отрезка
Предположим, мы поставили точку P. тогда координаты срединной точки будут
(x p +1, y p +1/ 2)
25
А значение функции F в этой точке d = F (x p +1, y p +1/ 2)
Если следующим поставленным пикселем будет E, тогда значение функции в новой срединной точке будет:
dnew = F (x p + 2, y p +1/ 2)
dnew −dold = F (x p + 2, y p +1/ 2) − F (x p +1, y p +1/ 2)
d= dnew −dold = dy = y2 − y1
Вслучае NE:
dnew = F (x p + 2, y p +3/ 2)
d = dy −dx = ( y2 − y1 ) −(x2 − x1 )
Рассмотрим начальную точку (x1,y1):
d start = F (x1 +1,y 1 +1/ 2) = (x1 +1− x1 )dy −( y1 +1/ 2 − y1 )dx =
= dy −dx / 2
Получив начальное значение d, мы сможем определить по его знаку положение следующего пиксела. Прибавив соответствующее d, мы получим значение функции для новой срединной точки и поставим второй пиксел. Продолжая цикл мы построим весь отрезок.
Единственная неприятность – деление на 2 в первом d. Получившееся значение скорее всего будет вещественным и потребует использование вещественных операций. Однако от этого можно избавиться, использовав следующее преобразование:
F ' (x, y) = 2F (x, y) d ' = 2d
dstart = 2dy −dx
d ' = 2 d
Тогда все d становятся целыми
Для построения произвольного отрезка перед построением необходимо проверить угол наклона и провести соответствующую зеркальную симметрию:
Если 0<=x2-x1<=y2-y1 то меняем местами x и y координаты.
Если тангенс угла наклона меньше 0, то отражаем относительно оси ординат x=-x а затем, если это необходимо, меняем x и y координаты.
Некоторые дополнительные вопросы построения отрезка
Порядок конечных точек
Одна из сложностей, возникающих по ходу построения отрезка, заключается в том, что отрезок от Т1 до Т2 должен содержать те же самые пикселы, что и отрезок Т2 – Т1, для того, чтобы представление линии было независимо от порядка задания концов. Единственный случай, в котором выбор пиксела зависит от направления построения линии, это прохождение отрезка точно через срединную точку, т.е. когда индикатор d равен нулю. Строя линию слева направо мы выберем пиксел E, а в противном случае пиксел W, но он же расположен на единичку выше первого! А значит, при построении линии справа налево необходимо в случае d=0 выбирать SW – пиксел.
26
Альтернативный способ решения проблемы – менять местами концевые точки, чтобы сканирование линии проходило всегда в одном направлении. Но этот метод не работает в случае использования стилей линии. Маска стиля всегда присоединяется к нижней левой точке, в независимости от направления, что не всегда приводит к ожидаемому эффекту. Кроме того, при построении примитива, один сегмент может быть построен с маской, расположенной слева направо, а следующий – с маской справа налево, и в общей вершине появляется артефакт.
Построение отрезка в случае отсечения (клипирования)
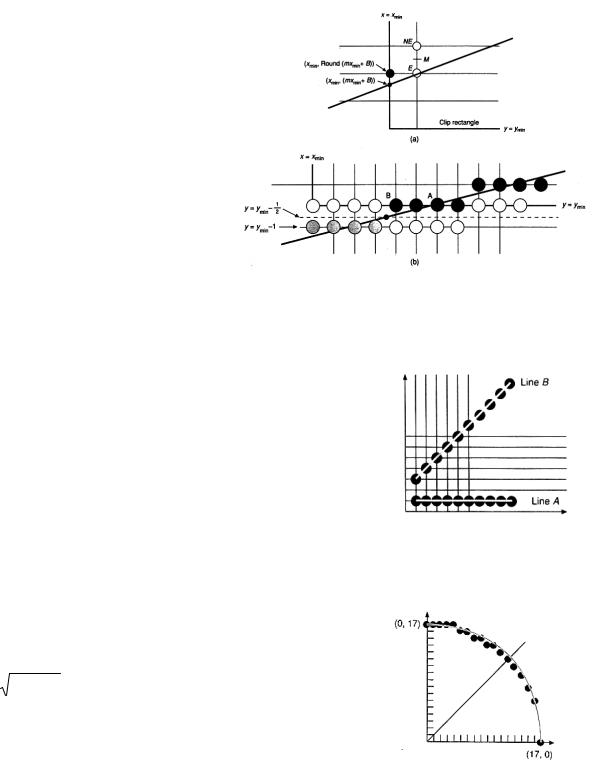
Некоторая модификация алгоритма необходима для поддержки отсечения. На рисунке (a) показан отрезок,
отсекаемый по левой границе клипирующего прямоугольника (x =min x). Точка пересечения с границей имеет целую x координату, но вещественную y. Пиксел
(xmin , Round (mxmin + B)) - тот же самый, который был бы выведен в отсутствии отсечения. Однако, приняв этот пиксел в качестве начального, нам необходимо соответствующим образом инициализировать индикатор по следующей срединной точке. Это требуется для получения правильной растеризации. В противном случае она
была бы отлична от ожидаемой, ведь наклон нового отрезка от (xmin , Round (mxmin + B)) до (x,y) не совпадает с наклоном исходного .
Еще более сложная ситуация представлена на рисунке (b) при пересечении отрезка с горизонтальной границей. Нам бы хотелось, чтобы были выведены все точки, соответствующие границе. Однако при простом вычислении точки пересечения отрезка и границы будет поставлена в качестве
первой точка A, а не B. Из рисунка видно, что первая точка, которую необходимо поставить – это ближайшая справа к точке пересечения отрезка с горизонталью y = ymin −1/ 2 . Значит, для правильного отсечения по нижней границе достаточно найти точку пересечения с линией y = ymin −1/ 2 и округлить значение x. Таким образом, первый пиксел B будет расположен в(Round(xymin −1/ 2 ), ymin ) .
Растровые алгоритмы построения окружности.
Окружность, как и отрезок, можно построить в лоб, используя математическое представление:
R2 = x2 + y 2 R = ± x2 + y 2
Тогда для каждого значения по оси абсцисс мы сможем вычислить соответствующее ему значение по ординате и поставить точку.
У данного метода существует несколько недостатков:

27
-Слишком сложные вычисления (операция извлечения корня квадратного)
-Пиксели неравномерно распределяются по окружности, и она оказывается неравномерно освещенной
От второго недостатка можно избавиться, если использовать представление окружности в полярных координатах:
x = R cosθ y = R sinθ
Тогда, пробегая все возможные значения θ с заданным шагом, для каждого из них мы определим координаты соответствующего ему пиксела, и закрасим его. На этот раз, т.к. мы каждый раз поворачиваем радиус на один и тот же угол, то пикселы будут равномерно распределены по окружности (рис.5). Однако, как и в предыдущем алгоритме, вычисление операции cos и sin слишком трудоёмки.
Задачу можно значительно упростить, если использовать то, что окружность является центрально-симметричной фигурой, а значит, если построить, к примеру, одну восьмую ее часть, то с помощью преобразования симметрии, можно достроить окружность полностью (рис.6).
Тогда можно использовать метод срединной точки для построения дуги окружности. Если за первый в дуге взять самый верхний пиксел, то следующим может быть лишь Е
или SE пиксел. И это справедливо для каждого пиксела в дуге. Если линия проходит выше срединной точки, то следующим пикселом будет E, если ниже – то SE.
Как и в случае отрезка, будем использовать задание окружности в неявном виде с помощью функции F(x,y):
Если F=0, то точка с данными координатами (x,y) расположена на окружности, если больше
F (x, y) =x2 +y 2 − R2
нуля – то вне окружности. А если меньше нуля – то внутри окружности.
(xp , yp )
Пусть поставленная точка имеет координаты:
Вычислим значение в соответствующей ей срединной точке: dold = F (x p +1, y p −1/ 2)
Если это d меньше нуля, т.е. окружность проходит выше срединной точки, то выбирается пиксел E, иначе выбирается пиксел SE.
Рассмотрим два случая (для двух различных выборов пиксела): 1) Если выбран пиксел E:
dnew = f (x p + 2, y p −1/ 2) = dold +(2x p +3) d E = (2x p +3)
2)Если выбрали пиксел SE, то он имеет координаты (x+1,y-1), а значит, соответствующая ему исрединная точка (x+2,y-3/2). И тогда:
28
dnew = dold +(2x p −2y p +5)
dSE = (2x p −2y p +5)
Таким образом, начиная с самой первой точки (верхняя точка окружности), мы определяем значение d для каждого нового пиксела, и, сравнив его значение с нулем, строим следующий пиксел в дуге окружности.
Рассчитаем значение d в начальной точке дуги (0,R):
F (1, R −1/ 2) =1+(R2 − R +1/ 4) − R2 = 5 / 4 − R
d0 = 5 / 4 − R
Значение d получается вещественным, что требует использования вещественных операций, которых желательно было бы избежать. Сделав замену h=d-1/4, получим, что h=1-R. Тогда необходимо сравнивать h с -1/4, но так как приращения d – целые числа, то сравнение можно заменить сравнением с нулем.
Построение дуги завершим, когда x станет примерно равен у. Вопрос с граничными точками соединения дуг решается отдельно в каждой реализации. Эти точки могут просто дублироваться.
Лабораторные основы
Цель работы: понять общие принципы построения изображения на примерах использования простейшего алгоритма построения отрезка, окружности и алгоритмов Брезенхема.
В этой работе будет выполнено:
1). рисование отрезка прямой линии, проходящего из точки с координатами ( xl, yl ) в точку с координатами ( х2, у2 ), реализуя простейший алгоритм,
2). рисование отрезка прямой линии, проходящего из точки с координатами ( xl, yl ) в точку с координатами ( х2, у2 ) по алгоритму Брезенхема для отрезка, 3). рисование окружности по простейшему алгоритму, 4). рисование окружности по алгоритму Брезенхема.
29
Лабораторная работа № 4:
" Построение кривых в форме Безье. Построение кривых в форме Фергюсона (Эрмита)"
Математические основы
Явный, неявный и параметрический вид задания функции.
Явный вид задания функции
у — f(x) - это явное выражение для у позволяет вычислять у при любом значении х (кроме описания вертикальных прямых , например, х=3 ) . Уравнение прямой линии у=2х+3 - пример явного задания функции.
Неявный вид задания функции f(x,y)=0 - неявное задание функции от х и у.
Пример неявного задания функции - уравнение окружности х +у — 1 = 0 с радиусом г=1. Чтобы в этом случае получить явный вид задания функции, уравнение х + у - 1=0 надо разбить на два уравнения:
для верхней половины окружности получим у = + ( 1 - х ) для нижней - у = - ( 1 + х )
Параметрический вид задания функции
В параметрическом виде задания функции х и у являются равноправными и представляются в виде функций от вспомогательного параметра t, то есть x = x(t),
У = У(0)
Параметрический вид, например, для уравнения окружности с радиусом г=1 будет записываться следующим образом:
X = COS t
У = sin t, где t лежит в интервале 0 < t < 2% .
Представление контуров в машинной графике
Наиболее распространены три типа представления контуров в машинной графике:
1.Кусочно-линейный
2.Линейно-круговой
3.Полиномиальный
Каждый из них имеет свои преимущества и свои недостатки.
1. Кусочно-линейный
По контуру кривой упорядоченно ( в порядке возрастания индекса !!! ) проставляются точки, которые затем соединяются отрезками прямых. В результате получаем массивы координат:
xi,x2,x3,......... ,х„ и уьу2,уз,.......,Уп•
2. Линейно-круговой
Используется, как правило, в оборудовании с программным управлением, где контуры описываются с помощью отрезков и дуг окружностей. Название этого типа представления контуров говорит само за себя.
30
3. Полиномиальный
Явный вид задания полинома:
у = ао + aix + 32Х +.... + anxn
Параметрический вид задания полинома:
х = аОх + ajxt + a2xt2 +....+ anxtn
у= аоу + aiyt + a2yt2 + ,... + anytn
Переход от представления контура в виде параметрической кубической кривой к кусочно-линейному представлению
Используется для упрощения вычисления размеров контура, например, для вычисления длины контура, площади внутри контура и т.д.
При конструировании пространственных форм (этим занимается геометрическое моделирование) возникают задачи трёхмерного представления поверхностей в пространстве. Рассмотрим одно из наиболее широко распространённых представлений, а , именно, параметрические кубические полиномы. Итак, почему кубический полином ( то есть кривая описывается многочленом третьей степени )? Потому что кубический многочлен является параметрической функцией наиболее низкой степени, с помощью которой можно представить кривую, описывающую реальную пространственную кривую. Имеется много способов представления параметрических бикубических кривых. Рассмотрим один из них:
кривые Безье .
Преимущество параметрических кубических кривых - нет разрывов.
Кривые Безье
Безье (1970) перегруппировал члены параметрического кубического многочлена Фергюссона и получил кривую следующего вида:
r= r(t) = (l-t)3po + 3t(l-t)2Pl+3t2(l-t)p2 + t3p3 ,
0 < t < l
Ценность этой кривой в том, что для своего построения она требуют задания всего 4 точек. Две из четырех прямых, соединяющих эти четыре точки, будут являться касательными для кривой Безье и их взаимное расположение определяет форму кривой Безье.
Свойства кривой Безье
1.Кривая Безье является гладкой кривой.
2.Начинается в 1-ой вершине ро массива из четырёх точек р0, pi, рг, рз, касается отрезка popi и заканчивается в последней точке р3, касаясь отрезка ргРз-
3.Лежит в выпуклой оболочке, порожденной массивом точек р0, pi, p2, Рз-
4.Симметрична, то есть сохраняет свою форму при перемене порядка вершин массива на
противоположный : р0, рь р2, Рз Рз, Рг, РнРо •
5.Если точки ро, pi, P2, Рз лежат на одной прямой , то кривая Безье совпадает с отрезком РоРз-
6.Если точки ро, pi, P2, Рз лежат в одной плоскости, то кривая Безье тоже лежит в этой плоскости.
7.Изменение положения хотя бы одной из четырёх опорных точек приводит к заметному изменению всей кривой Безье.
8.В уравнении, описывающем кривую Безье, нет свободных параметров - заданный набор из четырёх точек однозначно определяет кривую Безье, не давая возможности повлиять на её форму.
Кривые Безье
В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно).
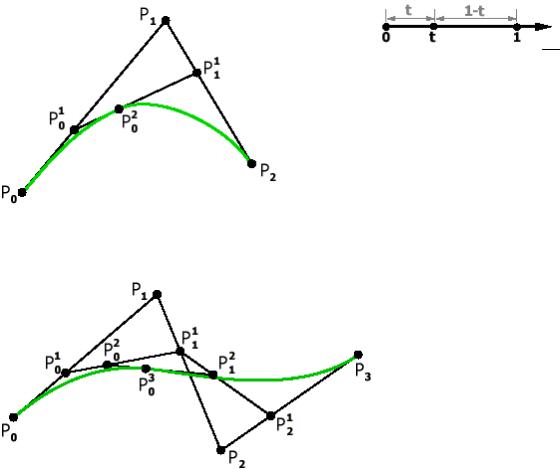
Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 8). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.
Рис. 1. Кривая Безье с 3 опорными точками.
Обозначим опорные точки как Pi ,i 0,2 , начало кривой положим в точке P0 (t=0), а конец в точке P2
(t=1), для каждого t [0,1] |
найдем точку P02 |
||||||||
P01 = (1−t) |
P |
0 |
+t 1 |
|
|
|
|
||
|
|
|
|
P |
|
|
|
|
|
P11 = (1−t) 1 |
+t 2 |
|
|
|
|
||||
|
|
|
P |
|
P |
|
|
|
|
P02 = (1−t)P01 +tP11 = |
|
P |
, |
||||||
(1−t)2 |
P |
0 + 2t(1−t) |
P |
+t2 |
2 |
||||
|
1 |
|
|||||||
таким образом, получим кривую второго порядка.
Теперь построим аналогичным методом кривую Безье с 4 опорными точками.
P01 = (1−t)P0 +tP1 P11 = (1−t)P1 +tP2 P21 = (1−t)P2 +tP3
P02 = (1−t)P01 +tP11 =
(1−t)2 P0 + 2t(1−t)P1 +t2 P2
P12 = (1−t)P11 +tP21 =
(1−t)2 P1 + 2t(1−t)P2 +t2 P3
Рис. 2. Кривая Безье с 4 опорными точками.
P03 = (1−t)P02 +tP12 = (1−t)2P12 + 2t(1−t)P12 +t2P12 =
(1−t)3 P0 +3t(1−t)2 P1 +3t2 (1−t)P2 +t3 P3
Кривые Фергюсона

Рис. 3. Кубическая интерполяция Эрмита.
32
Пусть заданы следующие условия:
f(xi ) =fi |
|
|
|
|
f(xi+1 ) =fi+1 |
|
|
|
|
,i 0, N −1 |
||||
f'(xi ) = mi |
||||
f'(xi+1 ) = mi+1 |
|
|
|
|
тогда для каждого i будем искать искомую функцию в
видеa*x3 + b*x2 +c*x +d . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно.
Класс C1
Лабораторные основы
Цель работы: программно проиллюстрировать свойства кривых Безье и Фергюсона.
Основные понятия, используемые в лабораторной работе: Явный, неявный и парамет-
рический вид задания функции. Представление контуров в машинной графике. Переход от представления контура в виде параметрической кубической кривой к кусочнолинейному представлению.Кривые в форме Безье. Кривые в форме Фергюсона.
Последовательность выполнения лабораторной работы
Задание 1. Нарисовать произвольно расположенные 4 точки - опорные точки для кривой Безье.
Задание 2. Последовательно соединить полученные 4 точки. Получим замкнутый контур, две стороны которого - будущие касательные для кривой Безье.
Задание 3. На форме заготовлены 4 метки: РО, PI, P2, РЗ, которые надо программно установить у одноименных точек. Для размещения метки на форме у определенной точки учтем, что,например, Х-координата метки РО - это свойство PO.Left, Y-координата - это свойство РО.Тор. В этом задании мы как бы развесим флажки на наши точки - "гвоздики", вбитые в форму для натяжения контура для кривой Безье.
Задание 4. Вписать в процедуру "Кривая Безье" параметрические формулы кривой Безье для координат X и Y .
Задание 5. Включить часы установкой свойства таймера Enabled.
Задание 6. Дописать цикл в процедуре для таймера, чтобы увидеть во времени построение кривой Безье.
Задание 7. Обратить внимание на работу процедуры FormMouseMove: вслед за движением мыши перемещается точка Р1 и, как следствие, перестраивается контур, а за ним и динамически перерисовывается кривая Безье.

33
Лабораторная работа № 5:
"Вычисление площади и периметра произвольного многоугольника"
Математические основы
Периметр
Периметром многоугольника называется сумма длин его сторон. В основу нахождения периметра многоугольника заложена теорема Пифагора.
0 |
xi |
xi+1 |
х |
|
|
|
|
yi+1 |
|
|
Ti=(xi, yi), где i=1, …, N |
yi |
|
|
|
|
|
|
N −1 |
|
|
|
P = ∑ (xi+1 − xi )2 +(yi+1 − yi )2 |
|
|
|
i=1 |
у
Многоугольник называется выпуклым, если он расположен по одну сторону от любой своей стороны, неограниченно продолженной.
Площадь
Трапецией называется четырёхугольник, две противоположные стороны которого параллельны, а две другие нет. Параллельные стороны называются основаниями.
b
h |
S = |
1 |
h(a +b) |
|
2 |
||||
|
|
|
||
|
a |
|
|
Метод трапеций для расчета площади многоугольника, представленного кусочнолинейным описанием
Суть метода заключается в том, что из вершин многоугольника выставляются перпендикуляры на ось х, образуя таким образом трапеции. Далее вычисляют площади этих трапеций. Одновременно при этом происходит вычитание "внешних площадей" (с момента, когда координаты по х начинают идти в обратную сторону), что приводит к вычислению истинной площади многоугольника.

|
|
|
|
|
34 |
|
|
0 |
xi |
xi+1 |
|
х |
|
||
|
|
|
|
|
|
|
|
yi+1 |
|
|
|
|
|
Ti=(xi, yi), где i=1, …, N |
|
|
|
|
|
|
|||
|
|
|
|
||||
yi |
|
|
|
|
|
N −1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
S = 0,5∑(xi − xi + 1)(yi + yi + 1) |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
h |
a+b |
у
Лабораторные основы
Цель работы: изучить способы вычисления площади и периметра замкнутых плоских деталей, представленных кусочно-линейным описанием.
Суть работы заключается в том, что в области рисования выставляются мышкой вершины многоугольника, координаты которых записываются в массив. Далее необходимо отобразить многоугольник, выставить перпендикуляры для наглядности и подсчитать площадь и периметр многоугольника. В конце работы необходимо доказать правильность расчётов.

35
Лабораторная работа № 6:
"Геометрические преобразования. Сдвиг, масштабирование, поворот, симметрия"
Математические основы
Двумерные преобразования
Преобразование точек
Точка представляется на плоскости двумя своими координатами, которые определяются как элементы матрицы размером 1х2 [х у]. В трехмерном пространстве используется матрица размером 1х3 [x у z]. Иначе говоря, точка может задаваться в виде вектор-столбца
x y
в двумерном пространстве или в виде
x y z
в трехмерном. Строку [х у] или столбец часто называют координатным вектором. Для формирования такого вектора используется матрица-строка, т. е. множество точек, каждая из которых определяет координатный вектор в некоторой системе измерения. Данное множество хранится в виде матрицы или массива чисел. Положением точек можно управлять путем манипулирования соответствующей матрицей. Линии, соединяющие точки, формируют отрезки, кривые и картинки.
Вкачестве элементов матрицы могут фигурировать различные величины: числа, сетки или коэффициенты системы уравнений. Правила в матричной алгебре определяют допустимые операции над элементами. Многие физические задачи удобно выражаются в матричном представлении. Для моделей физических систем задача обычно ставится следующим обра-
зом: даны матрицы [А] и [В], найти результирующую матрицу [Т], такую, что [А][Т] = [В]. В этом случае решением является матрица [Т] = [А]-1[В], где [А]-1 - матрица, обратная к квадратной матрице [А].
Вто же время матрицу [Т] можно интерпретировать как геометрический оператор. В этом случае для выполнения геометрического преобразования точек, представленных векторами положений в матрице [А], используется умножение матриц. Предположим, что матрицы [А] и [T] известны. Требуется определить элементы матрицы [В]. Представление [T] как геометрического оператора является основой математических преобразований, используемых в машинной графике.

36
Рассмотрим результаты умножения матрицы [х у], содержащей координаты точки Р, на матрицу общего преобразования размером 2х2:
[X][T] = [x y] |
a |
b |
[(ax + cy) (bx + dy)] |
|
c |
d |
|
Данная запись означает, что исходные координаты точки х и у преобразуются в х* и y*, где где х* = ах + су, у* = bх + dy. Представляют интерес значения х*, у* - координаты результирующей, преобразованной точки Р. Рассмотрим некоторые специальные случаи.
При а = d = 1 и с = b = 0 преобразование сведется к единичной матрице
[X][T] = [x y] |
1 |
0 |
[x y] = [x* y*] |
0 |
1 |
и координаты точки Р останутся неизменными. Как и следовало ожидать, в линейной алгебре умножение на единичную матрицу эквивалентно умножению на 1 в обычной алгебре.
В случае d = 1, b = c = 0
[X][T] = [x y] |
а |
0 |
[аx y] = [x* y*] |
|
0 |
1 |
|
где х* = ах - результат масштабирования координаты х. Эффект показан на рисунке 1.1,а.

37
Рассмотрим теперь еще случай b = с = 0, т.е.
[X][T] = [x y] |
а |
0 |
[аx yd] = [x* y*] |
|
0 |
d |
|
Данное преобразование вызывает изменение обеих координат х и у вектора Р (рис. 1.1,b). Если а <> d, то координаты масштабируются различным образом. При a = d > 1 происходит растяжение вектора Р или масштабирование координат. Если 0 < а = d < 1, то имеет место сжатие.
Если значение а или d отрицательное, то вектор отражается относительно координатных осей или относительно плоскости. Чтобы убедиться в этом, возьмем b = c = 0, d = 1 и а = 1, тогда
[X][T] = [x y] |
-1 |
0 |
[-x y] = [x* y*] |
0 |
1 |
ив результате получаем симметричное отражение относительно оси y (рис. 1.1,c). Если b = c
=0, а = 1, d = -1, то выполняется симметричное отражение относительно оси х. Если b = с = 0, а = d < 0, то происходит отражение относительно начала координат, это показано на рисунке 1.1,d, где a = -1, d =1. Заметим, что обе операции отражения и масштабирование зависят только от диагональных членов матрицы преобразования.
Рассмотрим теперь случай с недиагональными членами. Возьмем сначала значения a = d = 1, c = 0, тогда
[X][T] = [x y] |
1 |
b |
[x (bx + y)] = [x* y*] |
|
0 |
1 |
|
Заметим, что координата х точки Р осталась неизменной, тогда как координата y линейно зависит от исходных координат. Данное преобразование называется сдвигом (рис. 1.1,e). Аналогично, в случае, когда а = d = 1, b = 0, преобразование приведет к сдвигу пропорционально координате y (рис. 1.1,f). Таким образом, видно, что недиагональные члены матрицы преобразования создают эффект сдвига координат вектора точки Р.
Прежде чем закончить с преобразованием точек, разберем действие общего преобразования, когда начальный вектор лежит в точке начала координат, т.е.
[X][T] = [x y] |
a |
b |
[(ax + cy) (bx + dy)] |
c |
d |
или в случае начала координат,

|
|
|
38 |
|
|
[X][T] = [0 0] |
|
a |
b |
|
[0 0] = [x* y*] |
|
|
||||
|
|
c |
d |
|
|
Видно, что начало координат инвариантно относительно преобразования общего вида. Это ограничение устраняется при использовании однородных координат.
Преобразование параллельных линий
Прямую линию можно определить с помощью двух векторов, задающих координаты ее конечных точек. Расположение и направление линии, соединяющей две эти точки, может изменяться в зависимости от положения векторов.
Результатом преобразования двух параллельных линий с помощью (2х2)-матрицы снова будут две параллельные линии. Это можно увидеть, рассмотрев линию между точками [А] = [x1 y1], [В] = [х2 y2] и параллельную ей линию, проходящую между точками E и F. Покажем, что для этих линий любое преобразование сохраняет параллельность. Так как АВ, EF и A*B* и E*F* параллельны, то угол наклона линий АВ и EF определяется следующим образом:
y2 - y1
m =
x2 - x1
Преобразуем конечные точки АВ, воспользовавшись матрицей общего преобразования размером (2х2):
A |
[T] = |
x1 |
y1 |
|
a |
b |
= |
ax1 + cy1 bx1 + dy1 |
= |
x1* y1* |
= |
A* |
B |
|
x2 |
y2 |
|
c |
d |
|
ax2 + cy2 bx2 + dy2 |
|
x2* y2* |
|
B* |
Наклон прямой А*В* определяется следующим образом:
|
(bx2 + dy2) - (bx1 + dy1) |
b(x2 - x1) + d(y2 - y1) |
|
m* = |
= |
|
|
|
(ax2 + cy2) - (ax1 + cy1) |
|
a(x2 - x1) + c(y2 - y1) |
или
(y2 - y1)
|
b + d |
|
b + dm |
|
m* = |
|
(x2 - x1) |
= |
|
|
|
a + cm |
||
|
|
|
||
|
(y2 - y1) |
|
||
|
a + c |
|
|
|
|
|
(x2 - x1) |
|
|
Так как наклон m* не зависит от х1, х2, y1, y2, а m, а, b, с и d одинаковы для EF и AB, то m* одинаково для E*F* и А*В*. Таким образом, параллельные линии сохраняют параллельность и после преобразования. Это означает, что при преобразовании (2х2) параллелограмм преоб-

39
разуется в другой параллелограмм. Эти тривиальные выводы демонстрируют большие возможности использования матрицы преобразования для создания графических эффектов.
Преобразование пересекающихся прямых
Результатом преобразования с помощью (2х2)-матрицы пары пересекающихся прямых линий также будет пара пересекающихся линий. Проиллюстрируем это на примере двух прямых, заданных уравнениями:
y = m1x + b1
y= m2x + b2
Вматричном представлении эти уравнения будут иметь вид:
[X][T] = [x y] |
-m1 |
-m2 |
= [b1 b2] |
|
1 |
1 |
|
или
[X][M] = [B]
Если существует решение этой системы уравнений, то линии пересекаются, в противном случае они параллельны. Решение можно найти путем инверсии матрицы. В частности,
[Xi] = [xi yi] = [B][M] -1
Матрица, обратная [М], имеет следующий вид:
1
m2 - m1
-1
m2 - m1
m2
m2 - m1 -m1
m2 - m1
так как [M][M] -1 = [E], где [E] - единичная матрица. Поэтому координаты точки пересечения двух линий можно найти следующим образом:
|
|
|
1 |
|
m2 |
|
|
|
|
||
|
|
|
|
|
|
[Xi] = [xi yi] = [b1 b2] |
|
m2 |
- m1 |
|
|
|
|
|
|
m2 - m1 |
|
|
|
|
-1 |
|
-m1 |
|
|
|
|
|
|
|
|
m2 |
- m1 |
m2 - m1 |
|
|
40
b1 – b2 b1m2 - b2m1
[Xi] = [xi yi] =
m2 - m1 m2 - m1
Если обе линии преобразовать с помощью (2х2)-матрицы общего преобразования вида:
[T] = |
a |
b |
|
c |
d |
то их уравнения будут иметь вид
y* = m1*x* + b1* y* = m2*x* + b2*
Соответственно можно показать, что
mi* = |
|
b + dmi |
||
|
|
|
|
|
|
|
a + cmi |
|
|
и |
|
|
|
|
|
ad - bc |
|||
bi* = bi(d - cmi*) = bi |
|
|
|
где i = 1, 2. |
|
a + cmi |
|
||
Точка пересечения линий после преобразования отыскивается таким же образом, что и в случае исходных линий:
b1* - b2* b1*m2* - b2*m1*
[Xi*] = [xi* yi*] =
m2* - m1* m2* - m1*
Воспользовавшись тремя предыдущими выражениями, получим:
[Xi*] = [xi* yi*] = |
|
a(b1 - b2) + c(b1m2 – b2m1) |
|
b(b1 - b2) + d(b1m2 - b2m1) |
|
|
|
|
|
|
|
m2 - m1 |
|
m2 - m1 |
Возвращаясь теперь к точке пересечения [xi yi] исходных линий и применяя уже полученную матрицу преобразования, имеем
|
|
|
[xi* yi*] = [xi yi][T] = |
|
b1 – b2 |
|
b1m2 |
- b2m1 |
|
|
a |
b |
= |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
d |
||
|
m2 - m1 |
|
m2 |
- m1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
a(b1 - b2) + c(b1m2 – b2m1) |
b(b1 - b2) + d(b1m2 - b2m1) |
||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 - m1 |
|
|
|
|
m2 - m1 |
|
|
|
|||||

41
Сравнение уравнений точек пересечения исходных линий и преобразованных показывает, что они одинаковы. Итак, точка пересечения преобразуется точно в другую точку пересечения.
Поворот
Рассмотрим треугольник ABC (рис.1.2) и с помощью следующего преобразования повернем его на 90° против часовой стрелки относительно начала координат
[T] = |
0 |
1 |
-1 |
0 |
Если использовать матрицу (3 х 2), состоящую из координат x и y вершин треугольника, то можно записать
3 |
-1 |
|
0 |
1 |
|
= |
3 |
-1 |
|
|
|||||||
4 |
1 |
|
|
4 |
1 |
|||
|
-1 |
0 |
|
|||||
2 |
1 |
|
|
|
|
|
2 |
1 |
|
|
|
|
что является координатами результирующего треугольника A*B*C*. Поворот нв 180° относительно начала координат достигается путем следующего преобразования
[T] = |
-1 |
0 |
|
0 |
-1 |
а на 270° относительно начала координат - преобразованием

42
[T] = |
0 |
-1 |
1 |
0 |
Разумеется, что матрица тождественного преобразования
[T] = |
1 |
0 |
0 |
1 |
соответствует повороту вокруг начала координат на 0° или на 360°.
Как осуществить поворот вокруг точки начала координат на произвольный угол θ? Для ответа на этот вопрос рассмотрим вектор положения от начала координат до точки Р (рис. 1.3). Обозначим r - длину вектора, а φ - угол между вектором и осью х. Вектор положения поворачивается вокруг начала координат на угол θ и попадает в точку Р*. Записав векторы положений для Р и Р*, получаем:
Р = [х у] = [r cosφ r sinφ]
и
Р* = [x* у*] = [r соs(θ + φ) r sin(θ + φ].
Используя формулу для cos суммы углов, перепишем выражение для Р* следующим образом
Р* = [x* у*] = [r(cosφcosθ - sinφsinθ) r(соsφsinθ + sinφcosθ)].
Используя определения х и у, можно переписать Р* как
Р* = [x* у*] = [x cosθ - y sinθ x sinθ + y cosθ].
Таким образом, преобразованная точка имеет координаты x* = x cosθ - y sinθ y* = x sinθ + y cosθ.
Или в матричном виде
[X*] = [X][T] = [x* y*] = [x y] cosθ sinθ -sinθ cosθ

43
Итак, преобразование поворота вокруг точки начала координат на произвольный угол θ задается матрицей
[T] = cosθ sinθ -sinθ cosθ
Отражение
В то время как полный поворот на плоскости xy обычно осуществляется в двумерном пространстве относительно нормали к плоскости, отражение представляет собой тот же поворот на угол 180° в трехмерном пространстве и обратно на плоскость относительно оси, лежащей в плоскости xy. На рис. 1.4 приведены примеры двух отражений на плоскости треугольника DEF. Отражение относительно прямой y = 0 (ось x) получено с использованием матрицы
[T] = |
1 |
0 |
|
0 |
-1 |
В этом случае новые вершины треугольника D*E*F* будут определяться преобразованием
8 |
1 |
|
1 |
0 |
|
= |
8 |
-1 |
|
|
|||||||
7 |
3 |
|
|
7 |
-3 |
|||
6 |
2 |
|
0 |
-1 |
|
|
6 |
-2 |
|
|
|
|
|
Подобным образом отражение относительно оси y при x = 0 будет иметь вид

44
[T] = |
-1 |
0 |
|
0 |
1 |
Отражение относительно прямой y = x осуществляется с помощью матрицы
[T]= 0 1 1 0
Выполнив преобразования, получим координаты вершин треугольника D**E**F**
8 |
1 |
|
0 |
1 |
|
= |
1 |
8 |
|
|
|||||||
7 |
3 |
|
|
3 |
7 |
|||
6 |
2 |
|
1 |
0 |
|
|
2 |
6 |
|
|
|
|
|
Аналогичным образом отражение относительно оси x будет иметь вид
[T] = |
0 |
-1 |
-1 |
0 |
Масштабирование
Величина масштабирования определяется значением элементов исходной диагональной матрицы. Если матрица
[T]= 2 0 0 2
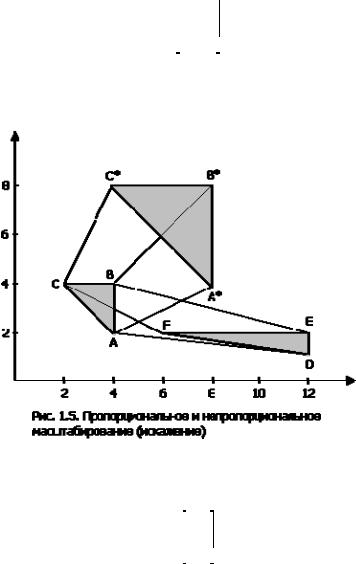
используется в качестве оператора воздействия на вершины треугольника, то имеет место «двукратное» расширение или равномерное масштабирование относительно точки начала координат. Если значения элементов не равны, то треугольник искажается, что проиллюстрировано на рис.1.5. Треугольник ABC, преобразованный с помощью матрицы
[T]= 2 0 0 2
переходит в пропорционально увеличенный треугольник A*B*C*. Тот же треугольник, но преобразованный с помощью матрицы
|
45 |
|
||
[T] = |
|
|
1/2 |
0 |
|
||||
|
|
|
0 |
3 |
переходит в треугольник DEF, имеющий искажение, вызванное разными коэффициентами масштабирования.
В общем случае при матрице
[T] = |
a |
b |
c |
d |
в которой а = d, b = с = 0, выполняется пропорциональное масштабирование; если a <> d, b = с = 0, то масштабирование будет проведено непропорционально. В первом случае для а = d > 1 происходит расширение, т.е. - увеличение изображения. Если а = d < 1, то происходит равномерное сжатие, т.е. фигура уменьшается. Непропорциональное расширение и сжатие возникают в зависимости от значений a и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.
Перемещения и однородные координаты
В предыдущих разделах был рассмотрен ряд преобразований, совершаемых с помощью (2х2)-матрицы общего преобразования. Среди них поворот, отражение, масштабирование, сдвиг и другие. Ранее отмечалось, что исходная система координат инвариантна по отношению ко всем перечисленным преобразованиям. Однако возникает необходимость изменять положение начала координат, т. е. преобразовывать каждую точку на плоскости. Этого можно достичь путем перемещения точки начала координат или любой другой точки на плоскости
x* = ax + cy + m, y* = bх + dy + n.

46
К сожалению, нельзя ввести константы перемещения m и n в (2х2)-матрицу преобразования, так как это не пространство!
Данное затруднение можно преодолеть, используя однородные координаты. Однородные координаты неоднородного координатного вектора [x y] представляют собой тройку [x' y' h], где x = x'/h, y = y'/h, а h - некоторое вещественное число. Заметим, что случай h = 0 является особым. Всегда существует один набор однородных координат вида [х у 1]. Мы выбрали эту форму, чтобы представить координатный вектор [х y] на физической плоскости хy. Все остальные однородные координаты представляются в виде [hx hy h]. Данные координаты не сохраняют однозначности, например, все следующие координаты [6 4 2], [12 8 4], [3 2 1] представляют физическую точку (3,2).
Матрица преобразования для однородных координат имеет размер 3х3. В частности,
a b 0 [T] = c d 0 m n 1
где действие элементов а, b, с и d верхней части (2х2)-матрицы точно соответствует действиям, рассмотренным ранее. Элементы m и n являются коэффициентами перемещения в направлениях x и y соответственно. Полная двумерная матрица преобразования имеет вид
|
1 |
0 0 |
|
[x* y* 1] = [x y 1] |
0 1 0 |
= [x+m y+n 1] |
|
|
m n 1 |
|
|
Отметим, что каждая точка плоскости и даже начало координат x = y = 0 теперь могут быть преобразованы.
Пространственные преобразования
Точка в трехмерном пространстве [х y z] представляется четырехмерным вектором
[x' y' z' h] = [x y z 1][T]
где [Т] является матрицей некоего преобразования. Как и ранее, преобразование из однородных координат в обычные задается формулой
|
|
x' |
y' |
z' |
|||
|
|||||||
[x* y* z* 1] = |
|
|
|
|
|
1 |
|
|
|
h |
|
h |
|
h |
|
|
|||||||
Обобщенную матрицу преобразования размерности 4х4 для трехмерных однородных координат можно представить в следующем виде:

47
|
a |
b |
с |
p |
[T] = |
d |
e |
f |
q |
g |
i |
j |
r |
|
|
l |
m |
n |
s |
Матрицу преобразования 4х4 можно разделить на четыре отдельные части. Верхння левая (3x3)-подматрица задает линейное преобразование в форме масштабирования, сдвига, отражения и вращения. Левая нижняя (1х3)-подматрица задает перемещение, а правая верхняя (3х1)-подматрица - перспективное преобразование. Последняя правая нижняя (1х1)- подматрица задает общее масштабирование. Общее преобразование, полученное после применения этой (4 х 4)-матрицы к однородному вектору и вычисления обычных координат, называется билинейным преобразованием. В общем случае данное преобразование осуществляет комбинацию сдвига, локального масштабирования, вращения, отражения, перемещения, перспективного преобразования и общего масштабирования.
Лабораторные основы
Цель работы: научиться использовать матрицы для таких двумерных преобразований, как сдвиг, масштабирование, поворот, симметрия (отражение относительно произвольно заданной точки и отрезка).
Основные понятия, используемые в лабораторной работе: Однородные координа-
ты. Двумерные преобразования (2D-преобразования). Матрицы. Суперпозиция простейших преобразований на языке матриц. Действия над матрицами.
Все изменения какого-нибудь объекта (кроме изменения цвета) на экране дисплея можно отнести к геометрическим преобразованиям, причем это относится и к изменениям при движении, и к статичным изменениям. Все превращения объекта можно представить как набор (суперпозицию) элементарных геометрических преобразований, выполненных в определённом порядке. В компьютерной графике всё, что относится к преобразованиям на плоскости, принято обозначать 2D, а к преобразованиям в пространстве - 3D.
Двумерные преобразования на плоскости
Сдвиг
На ху-плоскости есть точка Р с координатами (1,1). Сдвинем (перенесём) эту точку на новую позицию с координатами (2,6). Какие параметры этого простого геометрического преобразования? Параметра два: сдвиг по оси х, равный 1=2-1, и сдвиг по оси у, равный 5= 6-1.
Масштабирование
На ху-плоскости есть точка Р с координатами (2,6) (это точка из предыдущего примера). С помощью операции масштабирования вернём её на прежнее место, то есть на (1,1). Итак, во сколько раз надо сжать координаты точки Р? Очевидно, что по оси х в 2/1=2 раза, а по оси у в 6/1= 6 раз . Или растянуть в 1/2 и 1/6 раза соответственно.

48
Поворот
На ху-плоскости есть точка Р с координатами (1,1). Повернём точку Р относительно начала координат на угол φ=180°. Найдём её новые координаты. Получим, даже не прибегая к вычислениям (-1,-1). А если, например, φ = 25°, то "на глазок" получить новые координаты точки уже не получится. Выведем уравнения поворота точки на произвольный угол относительно начала координат. Пусть точка Р (х,у) поворотом на угол φ переводится в точку Р'(х',у'). В системе координат в Visual Basic углы по часовой стрелке - положительны. Поворот выполняется относительно начала координат, расстояния от него до точек Р и Р' пусть равны r. Получаем следующие соотношения.
Для точки Р: х = r cos α , у = r sin α .
Для точки Р': х' = r cos (α + φ) = r cos α cos φ - r sin α sin φ, у' = r sin (α + φ) = r cos α sin φ + r sin α cos φ. х' = х cos φ - у sin φ
у' = х sin φ + у cos φ
Однородные координаты
Однородными координатами точки называется тройка одновременно не равных нулю чисел. В компьютерной графике однородные координаты вводятся так: произвольной точке Р(х, у) на плоскости ставится в соответствие точка Р(х, у, 1) в пространстве.
Соединим прямой точки О(0, 0, 0) и Р(х, у, 1). Любую точку этой прямой, соединяющей начало системы координат О(0, 0, 0) с точкой Р(х, у, 1), можно задать тройкой чисел (hx, hy, h), где h≠0. Проведём плоскость z = 1, параллельную плоскости ху, через точку Р(х, у, 1). Прямая, соединяющая точки О и Р, пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху. Таким образом, между произвольной точкой с координатами (х, у) и множеством троек чисел (hx, hy, h), где h≠0, устанавливается взаимно однозначное соответствие, позволяющее считать числа hx, hy, h новыми (однородными) координатами этой точки. В компьютерной графике вслед за проективной геометрией для однородных координат принято обозначение:
х : у : 1
или в более общем случае:
х1 : х2 : х3 (числа х1, х2, х3 не должны быть равны нулю одновременно). Однородные координаты удобны для программирования геометрических преобразований. При помощи однородных координат и матриц 3-го порядка можно выполнить любое геометрическое преобразование в плоскости. Любое геометрическое преобразование выполняется следующим действием:
a b 0 (x', y', 1) = (x, y, 1) c d 0 e f 1

49
x'=xa+yc+1e; y'=xb+yd+1f
Для каждого геометрического преобразования существует своя матрица.
Рассмотрим конкретный пример сдвига. На ху-плоскости есть точка Р с координа-
тами (1,1). Требуется сдвинуть (перенести) эту точку на 1 единицу по оси х и на 5 единиц по оси у. Для сдвига существует следующее матричное выражение:
1 |
0 |
0 |
(x', y', 1) = (x, y, 1) 0 |
1 |
0 |
d x |
d y |
1 |
Здесь dx=1, dy=5. Следовательно, получаем: x'=1×1+1×0+1×1=2; y'=1×0+1×1+1×5=6
Суперпозиция
На примере поворота некоторой фигуры относительно заданной точки, рассмотрим мно-
жественные преобразования с помощью матричных выражений.
α
yв
xв
Для этого необходимо вначале переместить фигуру в начало координат, затем повернуть на необходимый угол α и вернуть обратно в точку вращения. Пусть координаты преобразованной фигуры будут xi''' , yi''' (три действия – три штриха), а исходной - xi , yi . Приведём решение.
|
1 |
0 |
0 |
cosα |
sinα |
0 |
1 |
0 |
0 |
|
(xi''' , yi''' ,1)= (xi , yi ,1) 0 |
1 |
0 |
−sinα |
cosα |
0 |
0 |
1 |
0 |
||
|
− xв |
− yв |
1 |
0 |
0 |
1 |
xв |
yв |
1 |
|
xi' |
= xi − xв ; yi' = yi − yв |
|
|
|
|
|
|
|
|
|
xi'' |
= (xi − xв ) cosα −( yi |
− yв ) sinα ; |
yi'' |
= (xi − xв ) sinα +( yi − yв ) cosα |
||||||
xi''' |
= (xi − xв ) cosα −( yi |
− yв ) sinα + xв ; |
yi''' = (xi − xв ) sinα +( yi − yв ) cosα + yв |
|||||||

50
Краткая информация из тригонометрии
Формулы сложения
Cos(α+β) = cos α cos β - sin α sin β Sin(α+β) = sin α cos β - cos α sin β
Некоторые значения тригонометрических функций
α |
0° |
30° |
45° |
60° |
90° |
180° |
|
|
|
|
|
|
|
cos α |
1 |
√3/2 |
√2/2 |
½ |
0 |
-1 |
|
|
|
|
|
|
|
sin α |
0 |
1/2 |
√22 |
√3/2 |
1 |
0 |
|
|
|
|
|
|
|
Матрицы преобразований на плоскости. Общий вид
1. Матрица сдвига (translation)
1 |
0 |
0 |
[T] = 0 |
1 |
0 |
d x |
d y |
1 |
dx - сдвиг по оси х, dy - сдвиг по оси у
2. Матрица масштабирования (dilatation)
|
Sx |
0 |
0 |
[D] = |
0 |
Sy |
0 |
|
0 |
0 |
1 |
sx - коэффициент растяжения/сжатия по оси х; sy - коэффициент растяжения/сжатия по оси у. Если sx = sy - масштабирование однородно и пропорции объекта сохраняются. Если sx≠sy - масштабирование неоднородно и пропорции объекта не сохраняются.
3. Матрица поворота (rotation)
cosϕ |
sinϕ |
0 |
[R] = −sinϕ |
cosϕ |
0 |
0 |
0 |
1 |
φ- угол поворота объекта относительно начала координат.
4.Матрица симметрии (reflection)
1 0 0 [Mox] = 0 −1 0 0 0 1

51
Матрицы преобразований в пространстве. Общий вид
1. Матрица сдвига
|
1 |
0 |
0 |
0 |
[T] = |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
d x |
d y |
d z |
1 |
2. Матрица масштабирования
|
sx |
0 |
0 |
0 |
[D] = |
0 |
sy |
0 |
0 |
0 |
0 |
sz |
0 |
|
|
0 |
0 |
0 |
1 |
3. Матрицы поворота на угол α
|
cosα |
sinα |
0 |
0 |
|
|
1 |
|
0 |
0 |
0 |
|
|
cosα |
0 |
−sinα |
0 |
|||
[Roz] = |
−sinα cosα |
0 |
0 |
[Rox] = |
0 |
cosα |
sinα |
0 |
[Roy] = |
|
0 |
1 |
0 |
0 |
||||||
|
0 |
0 |
|
1 |
0 |
0 |
−sinα |
cosα |
0 |
|
sinα |
0 |
cosα |
0 |
||||||
|
|
0 |
0 |
|
0 |
1 |
|
|
0 |
|
0 |
0 |
1 |
|
|
|
0 |
0 |
0 |
1 |
4. Матрицы симметрии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
0 |
0 |
0 |
|
|
|
−1 0 0 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
|
||
[Mxy] = |
0 |
1 |
0 |
0 |
|
[Myz] = |
0 1 0 |
0 |
[Mzx] = |
0 |
−1 0 |
0 |
|
|
|
|||||
0 0 −1 0 |
|
0 0 1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
||||||||||
|
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
|
|
|

52
Лабораторная работа № 7:
"Аппроксимация. Mетод наименьших квадратов. Интерполяция. Метод Лагранжа."
Математические основы
Интерполяция - построение кривой, проходящей через контрольные точки. Аппроксимация - приближение кривой (не обязательно проходит точно через данные точки, но удовлетворяет некоторому заданному свойству относительно этих точек).
Интерполяция
Постановка задачи:
Дано: f(xi) =fi . xi < xi+1 i 0, N .
Построить функцию f(x), удовлетворяющую этому условию.
Рис. 4. Постановка задачи.
1) Интерполяционный многочлен Лагранжа
|
|
|
N |
|
|
|
N |
|
|
|
N |
|
N |
∏(x −xj) |
|
|
∏(x −xj) |
|
|
||
LN (x) = ∑fi |
N(x) = ∑fi |
j=0,j≠i |
|
; |
N(x) = |
j=0,j≠i |
|
; |
N(xj) = δij |
|
N |
|
N |
|
|||||||
i=0 |
Li |
i=0 |
∏(x −x ) |
|
Li |
∏(x −x ) |
|
Li |
||
|
|
|
i |
k |
|
|
i |
k |
|
|
|
|
|
k=0,k≠i |
|
|
|
k=0,k≠i |
|
|
|
Получаем непрерывную функцию, проходящую через все точки.
Минусы:
1)Требует значительного объема вычислений для нахождения значения функции в произвольной точке.
2)Неопределенное поведение построенной функции между узлами, в частности можно привести следующие результаты:
1916 Бернштейн : LN(x) 
 x, N → ∞
x, N → ∞
1925 Рунге : LN(x)  (1+25x2 )−1 C∞, N → ∞
(1+25x2 )−1 C∞, N → ∞
Далее будем рассматривать интерполирующие функции, которые задаются отдельно на каждом отрезке [xi ,xi+1 ],i 0, N −1, что позволяет лучше учитывать локальное поведение тре-
буемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид).

2) Кусочно-линейная интерполяция
Рис. 5. Кусочно-линейная интерполяция.
3) Кубическая интерполяция Эрмита
Рис. 6. Кубическая интерполяция Эрмита.
Проблемы:
1)Хотелось бы C2 , а не только C1
4)Сплайны
53
Интерполяция следующей кусочно-линейной функ-
цией:
f(x) = fi+1 * (x −xi ) −fi * (x −xi+1 ) , xi+1 −xi
x [xi ,xi+1 ],i 0, N −1
Класс C0
Пусть заданы следующие условия:
f(xi ) =fi |
|
|
|
|
f(xi+1 ) =fi+1 |
|
|
|
|
,i 0, N −1 |
||||
f'(xi ) = mi |
||||
f'(xi+1 ) = mi+1 |
|
|
|
|
тогда для каждого i будем искать искомую функцию в
видеa*x3 + b*x2 +c*x +d . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно.
Класс C1
Сплайн - кусочный полином степени K с непрерывной производной степени K-1 в точках соединения сегментов.
Далее нас будут интересовать кубические сплайны.
Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной кривой, которую затем чертили по этой линейке (см. Рис. 7) Форма такой линейки, если ее рассматривать как функцию y(x),
будет удовлетворять уравнению Эйлера-Бернулли: y''(x) = ME(*xI) ,где M(x) - момент изгиба
вдоль рейки, E - модуль Юнга. зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки подпорками, то момент
изгиба на каждом отрезке [xi ,xi+1 ],i 0, N −1 меняется по линейному закону: M(x) = A*x +
B , подставляя в исходное уравнение получаем: y''(x) = A * x + B , дважды интегрируя полу-
E*I
чаем уравнение кривой на данном

54
отрезке: y(x) = a*x3 + b*x2 +c*x +d ; таким обра-
зом форма физического сплайна описывается кусочным кубическим полиномом.
Теперь рассмотрим задачу построения системы таких кубических полиномов для всего отрезка [x0 ,xN ]
Рис. 7. Сплайн.
1)Для N отрезков имеем 4N коэффициентов: y(x) =ai *x3 +bi *x2 +ci *x +di, для
x[xi ,xi+1 ],i 0, N −1;
2)Условия f(xi) =fi ( i 0, N ) дают 2N уравнений;
3)Требование C1 в точках xi ( i 1, N −1) дает N-1 уравнений;
4)Требование C2 в точках xi ( i 1, N −1) дает N-1 уравнений.
Итого имеем 4N-2 уравнения; для того чтобы система была определенной, необходимы еще 2 уравнения; их можно вывести, например, из заданных значений производных на границах или из условия периодичности. При корректно заданных условиях линейная относительно
ai , bi ,ci , di ,i 0, N −1 система имеет единственное решение. Подробнее смотри в
Ошибка! Источник ссылки не найден..
Аппроксимация
1) Кривые Безье
В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно).
Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 8). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.
Рис. 8. Кривая Безье с 3 опорными точками.
Обозначим опорные точки как Pi ,i 0,2 , начало кривой положим в точке P0 (t=0), а конец в точке P2
(t=1), для каждого t [0,1] |
найдем точку P02 |
||||||||
P01 = (1−t) |
P |
0 |
+t 1 |
|
|
|
|
||
|
|
|
|
P |
|
|
|
|
|
P11 = (1−t) 1 |
+t 2 |
|
|
|
|
||||
|
|
|
P |
|
P |
|
|
|
|
P02 = (1−t)P01 +tP11 = |
|
P |
, |
||||||
(1−t)2 |
P |
0 + 2t(1−t) |
P |
+t2 |
2 |
||||
|
1 |
|
|||||||
таким образом, получим кривую второго порядка.
Теперь построим аналогичным методом кривую Безье с 4 опорными точками.

55
P01 = (1−t)P0 +tP1 P11 = (1−t)P1 +tP2 P21 = (1−t)P2 +tP3
P02 = (1−t)P01 +tP11 =
(1−t)2 P0 + 2t(1−t)P1 +t2 P2
P12 = (1−t)P11 +tP21 =
(1−t)2 P1 + 2t(1−t)P2 +t2 P3
Рис. 9. Кривая Безье с 4 опорными точками.
P03 = (1−t)P02 +tP12 = (1−t)2P12 + 2t(1−t)P12 +t2P12 =
(1−t)3 P0 +3t(1−t)2 P1 +3t2 (1−t)P2 +t3 P3
Можно продолжать подобные построения и для большего числа узлов, получая аналогичные выкладки. Запишем общее аналитическое представление для кривой Безье с N+1 опорной точкой:
n |
|
|
n |
|
|
|
n |
n |
n |
i |
|
n−i |
|
|
n! |
|
|
i |
|
n−i |
|
P |
(t) = ∑ |
i Bi |
(t) , где Bi |
(t) =Ci |
t |
(1−t) |
|
= |
|
|
|
|
t |
(1−t) |
|
, где |
|||||
|
|
− |
)! |
|
|||||||||||||||||
|
|
|
=0P |
|
|
|
|
|
|
|
!( |
|
|
|
|
||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i n |
i |
|
|
|
|
||
n |
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ci |
= |
|
|
|
|
|
- биномиальные коэффициенты, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
− |
i)! |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
i!(n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Bin (t) называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна).
Лабораторные основы
Цель работы: изучить интерполяционный многочлен Лагранжа и научиться вычислять параметры для аппроксимирующих функций, чтобы строить графики зависимостей для произвольных наборов точек.
Основные понятия, используемые в лабораторной работе: Аппроксимация и ин-
терполяция: различие и сходство. Метод наименьших квадратов. Многочлен Лагранжа.
Под аппроксимацией обычно понимают операцию сглаживания, которая призвана уменьшить осцилляции, обусловленные неверными значениями некоторых координат. Задача аппроксимации возникает тогда, когда по заданному массиву точек [xi, yi], где i=0, 1, …, m, требуется построить функцию, проходящую не через заданные точки, а вблизи них, и изменяющуюся достаточно плавно.
δi |
Аппроксимация: δi → min |
|
Интерполяция: δi = 0 |
56
Метод наименьших квадратов
Предположим, у нас имеется набор экспериментальных точек зависимости Y от X . Возникает вопрос, как по этим экспериментальным точкам наилучшим образом воспроизвести зависимость Y от X? Для решения подобных задач обычно применяется расчетный метод, известный под названием "Метод наименьших квадратов". Этот метод дает возможность при заданном типе зависимости Y=f(X) так выбрать ее числовые параметры, чтобы график зависимости Y=f(X) наилучшим образом отображал экспериментальные данные. Тип зависимости Y=f(X), как правило, выбирается исходя из внешнего вида полученного набора точек. Он может быть линейным, квадратичным, экспоненциальным и т.д. . В методе наименьших квадратов под условием «наилучшим образом» понимают следующее требование: "Сумма квадратов отклонений экспериментальных точек от сглаживающей кривой должна быть минимальной".
Рассмотрим линейную зависимость. Пусть имеется набор из n экспериментальных точек с координатами (х1, y1), (х2, у2), ..., (хn, уn). Предполагается, что точки отображают линейную зависимость. Требуется подобрать по методу наименьших квадратов коэффициенты а и b линейной функции у = ах + b.
Решение. Запишем у как функцию не только аргумента х, но и параметров а и b (так как величины а и b неизвестны ):
у = f (х; a, b) = ax + b |
(1) |
Требуется выбрать а и b так, чтобы выполнялось условие: "Сумма квадратов отклонений экспериментальных точек от построенной линейной зависимости должна быть минимальной", то есть для набора n экспериментальных точек должно быть выполнено условие :
∑n [yi − f (xi )]2 |
= min (2) |
i=1 |
|
или |
|
∑n [yi − f (axi +b)]2 = min
i=1
где уi - значение у-координаты i-ой точки из набора экспериментальных точек, хi - значение x-координаты i-ой точки из набора экспериментальных точек, (ахi + b) - значение функции у = ах + b в i-ой точке.
Найдём значения а и b, при которых левая часть выражения (2) обращается в минимум. Для этого продифференцируем её по а и b; приравняем производные нулю:
|
|
n |
dy |
= 0 ; |
n |
dy |
= 0 |
(3) |
||
|
∑[yi − y(xi )] |
|
∑[yi − y(xi )] |
|
||||||
|
i=1 |
da i |
|
i=1 |
db i |
|
|
|||
dy |
- значение частной производной функции у(х) = ах + b по параметру а в точке c |
|||||||||
где |
|
|
||||||||
|
||||||||||
da i |
|
|
|
|
|
|
|
|
||

|
57 |
dy |
- значение частной производной функции по параметру b. |
координатами (хi, уi) , а |
|
db i |
|
Система уравнений (3) содержит столько уравнений, сколько неизвестных коэффициентов в искомой зависимости. В нашем случае их два – а и b. Продифференцируем (1) по а и b, получим:
dy |
= |
d (ax +b) |
= x ; |
dy |
= xi |
||
|
|
|
|
|
|||
da |
da |
|
|||||
|
|
da i |
|
||||
|
|
|
|
|
|
|
(4) |
dy |
= |
d (ax +b) |
=1 ; |
dy |
=1 |
||
db |
db |
|
|
|
|||
|
|
db i |
|
||||
Подставим выражения (4) в (3) и получим два уравнения для определения а и b:
∑n [yi −(axi +b)] xi = 0
i=1
(5)
∑n [yi −(axi +b)] 1 = 0
i=1
Раскроем скобки, просуммируем и получим:
∑n |
xi yi −a∑n |
xi2 −b∑n |
xi |
= 0 |
(6) |
|
i=1 |
i=1 |
i=1 |
|
|
|
|
∑n |
yi −a∑n |
xi |
−bn = 0 , |
где n – число точек |
||
i=1 |
i=1 |
|
|
|
|
|
Получили систему из двух уравнений с двумя неизвестными, которая легко решается. Рассмотрим теперь конкретный пример. Пусть имеется набор из 3 экспериментальных
точек с координатами (1,1), (2,2) и (3,0). Предполагается, что точки отображают линейную зависимость. Требуется найти коэффициенты а и b для линейной функции у = ах + b.
|
|
Решение. |
|
Xi |
|
Уi |
Воспользуемся системой уравнений (6) и подставим в неё координаты экспери- |
|
|||
1 |
|
1 |
ментальных точек. Получаем следующую систему уравнений: |
2 |
|
2 |
(1 1+2 2 +3 0) −a(12 +22 +32 ) −b(1+2 +3) = 0 |
3 |
|
0 |
(1+2 +0) −a(1+2 +3) −b 3 = 0 |
14a +6b =5
2a +b =1
Решаем и получаем a = -0.5, b = 2. Таким образом, вид линейной функции: у = - 0.5 х + 2 .

58
Под интерполяцией понимают построение гладкой функции, проходящей через все заданные точки. Для этого применяют интерполяционные кубические сплайны, NURBSсплайны, B-сплайны и т.п.
Интерполяционный многочлен Лагранжа
Многочлен Лагранжа в основном используют для учебных целей, хотя его можно применять и на практике (в случае небольшого количества точек).
По заданному массиву точек (xi, yi), где i=0, 1, …, m
Lm |
интерполяционный многочлен Лагранжа определяется |
|
|
|
формулой: |
x0 x |
xm |
m |
ϕm (x) |
|
m |
|
|
Lm (x) = ∑yi |
|
, где ϕm (x) = ∏(x − xi ) |
|
|
|
' |
(xi ) |
||
|
|
i=0 |
(x − xi )ϕm |
i=0,i≠m |
m
ϕm' (xi ) = ∏(xm − xi ) i=0,i≠m
Рассмотрим конкретный пример. Распишем интерполяционный многочлен Лагранжа для трёх точек (i=0,…, 2): Lm (x) = y0 L0 + y1 L1 + y2 L2
L0 |
= |
|
(x − x1 ) (x − x2 ) |
|||
|
(x0 |
− x1 ) (x0 − x2 ) |
||||
|
|
|
||||
L1 |
= |
|
(x − x0 ) (x − x2 ) |
|
||
(x1 |
− x0 ) (x1 − x2 ) |
|||||
|
|
|||||
L2 |
= |
|
(x − x0 ) (x − x1 ) |
|||
|
(x2 |
− x0 ) (x2 − x1 ) |
||||
|
|
|
||||

59
Лабораторная работа № 8:
"Закраска произвольных областей"
Математические основы
Простой алгоритм заполнения с затравкой
В алгоритмах заполнения с затравкой предполагается, что известен хотя бы один пиксел из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пикселы, принадлежащие внутренней области. Области могут быть либо внутренне-, либо гра- нично-определенными. Если область относится к внутренне-определенным, то все пикселы, принадлежащие внутренней части, имеют один и тот же цвет или интенсивность, а все пикселы, внешние по отношению к области, имеют другой цвет. Это продемонстрировано на рис. 2.12. Если область относится к гранично-определенным, то все пикселы на границе области имеют выделенное значение или цвет, как это показано на рис. 2.13. Ни один из пикселов из внутренней части такой области не может иметь это выделенное значение. Тем не менее пикселы, внешние по отношению к границе, также могут иметь граничное значение. Алгоритмы, заполняющие внутренне-определенные области, называются внутреннезаполняющими, а алгоритмы для гранично-определенных областей - граничнозаполняющими. Далее будут обсуждаться гранично-заполняющие алгоритмы, однако соответствующие внутренне-заполняющие алгоритмы можно получить аналогичным образом.
Внутреннеили гранично-определенные области могут быть 4-или 8-связными. Если область 4-связная, то любого пиксела в области можно достичь с помощью комбинации движений только в 4 направлениях: налево, направо, вверх, вниз. Для 8-связной области пиксела можно достичь с помощью комбинации движений в двух горизонтальных, двух вертикальных и 4 диагональных направлениях (рис. 2.14).
Далее речь в основном пойдет об алгоритмах для 4-связных областей, однако их можно легко переделать для 8-связных областей, если заполнение проводить не в 4, а в 8 направлениях.
60
Используя стек, можно разработать простой алгоритм заполнения гранично-определенной области. Стек - это просто массив или другая структура данных, в которую можно последовательно пометить значения и из которой их можно последовательно извлекать. Когда новые значения добавляются или помещаются в стек, все остальные значения опускаются вниз на один уровень. Когда значения удаляются или извлекаются из стека, остальные значения всплывают или поднимаются вверх на один уровень. Такой стек называется стеком прямого действия. Простой алгоритм заполнения с затравкой можно представить в следующем виде:
Простой алгоритм заполнения с затравкой и стеком.
Поместить затравочный пиксел в стек Пока стек не пуст Извлечь пиксел из стека
Присвоить пикселу требуемое значение Для каждого из соседних к текущему 4-связных пикселов проверить: является ли он гра-
ничным пикселом или не присвоено ли уже пикселу требуемое значение. Проигнорировать пиксел в любом из этих двух случаев. В противном случае поместить пиксел в стек.
Приведем более формальное изложение алгоритма, в котором предполагается существование затравочного пиксела и гранично-определенной области:
Затравка(х, у) - выдает затравочный пиксел Push - процедура, которая помещает пиксел в стек
Pop - процедура, которая извлекает пиксел из стека
Пиксел(х, у) = Затравка(х, у) |
|
Push Пиксел(х, у) |
/ инициализируем стек |
while (стек не пуст) |
|
Pop Пиксел(х, у) |
/ извлекаем пиксел из стека |
if Пиксел(х, у) <> Нов_значение then |
|
Пиксел(х, у) = Нов_значение |
|
end if |
|
if (Пиксел(х + 1, у) <> Нов_значение and Пиксел(х + 1, у) <> Гран_значение) then Push Пиксел (х + 1, у)
if (Пиксел(х, у + 1) <> Нов_значение and Пиксел(х, у + 1) <> Гран_значение) then Push Пиксел (х, у + 1)
if (Пиксел(х - 1, у) <> Нов_значение and Пиксел(х - 1, у) <> Гран_значение) then Push Пиксел (х - 1, у)
if (Пиксел(х, у — 1) <> Нов_значение and Пиксел(х, у - 1) <> Гран_значение) then Push Пиксел (х, у - 1)
end if end while
Пример 2.3. Алгоритм заполнения многоугольника с затравкой. В качестве примера применения алгоритма рассмотрим гранично-определенную область, содержащую дыру. Она изображена на рис. 2.15.

61
Вершины многоугольника заданы пикселами (1,0), (7,0), (8,1), (8,4), (6,6), (1,6), (0,5) и (0,1).
Внутренняя дыра определяется пикселами (3,2), (5,2), (5,3), (3,3). Затравочный пиксел — (4,4). Порядок заполнения указан на рисунке линией со стрелками. Числа в квадратике пиксела показывают позицию в стеке, занимаемую пикселом. Когда обработка доходит до пиксела (3,1), все окружающие его 4-связные пикселы либо уже заполнены, либо являются граничными. Поэтому ни один из пикселов не помещается в стек. Глубина стека в этот момент равна 15. В стеке находятся пикселы (7,1), (7,2), (7,3), (6,5), (7,4), (6,5), (3,1), (1,2), (1,3), (1,4), (2,5), (3,5), (4,5), (5,4).
После удаления из стека пиксела (7,1) заполняется колонка (7,1), (7,2), (7,3), (7,4), при этом ни один новый пиксел в стек не добавляется. Для пиксела (7,4) снова все 4-связные окружающие пикселы либо уже заполнены, либо являются граничными. Обращаясь к стеку, алгоритм извлекает пиксел (6,5), его заполнение завершает заполнение всего многоугольника. Дальнейшая o6работка происходит без какого-либо заполнения, и когда стек становится пустым, алгоритм завершает работу.
Построчный алгоритм заполнения с затравкой
Как видно из предыдущего примера, стек может стать довольно большим. Еще один недостаток предыдущего алгоритма - стек зачастую содержит дублирующую или ненужную информацию. В построчном алгоритме заполнения с затравкой размер стека минимизируется за счет хранения только одного затравочного пиксела для любого непрерывного интервала на сканирующей строке. Непрерывный интервал - это группа примыкающих друг к другу пикселов (ограниченная уже заполненными или граничными пикселами). Мы для разработки алгоритма используем эвристический подход, однако также возможен и теоретический подход, основанный на теории графов.
Данный алгоритм применим к гранично-определенным областям. Гранично-определенная 4- связная область может быть как выпуклой, так и не выпуклой, а также может содержать дыры. В области, внешней и примыкающей к нашей гранично-определенной области, не должно быть пикселов с цветом, которым область или многоугольник заполняется. Схематично работу алгоритма можно разбить на четыре этапа.
62
1.Затравочный пиксел на интервале извлекается из стека, содержащего затравочные пикселы.
2.Интервал с затравочным пикселом заполняется влево и вправо от затравки вдоль сканирующей строки до тех пор, пока не будет найдена граница.
3.В переменных Хлев и Хправ запоминаются крайний левый и крайний правый пикселы интервала.
4.В диапазоне Хлев <= x <= Xправ проверяются строки, расположенные непосредственно над и под текущей строкой. Определяется, есть ли на них еще не заполненные пикселы. Если такие пикселы есть (т. е. не все пикселы граничные, или уже заполненные), то в указанном диапазоне крайний правый пиксел в каждом интервале отмечается как затравочный и помещается в стек.
5.При инициализации алгоритма в стек помещается единственный затравочный пиксел, работа завершается при опустошении стека.
Как показано в примере ниже, алгоритм справляется с дырами и зубцами на границе. Ниже приводится более подробное описание алгоритма на псевдокоде:
Затравка (х,у) - выдает затравочный пиксел
Pop - процедура, которая извлекает пиксел из стека Push - процедура, которая помещает пиксел в стек
Push Затравка (х, у) |
/ инициализируем стек |
while (стек не пуст) |
|
Pop Пиксел (х, у)
Пиксел (х, у) = Нов_значение Врем_х = х
х = х + 1
while Пиксел (х, у) <> Гран_значение Пиксел (х, у) = Нов_значение х = х + 1
end while
Хправ = х — 1
х= Врем_х
х= х — 1
while Пиксел (х, у) <> Гран_значение Пиксел (х, у) = Нов_значение х = х — 1
end while
Хлев = х + 1
х= Врем_х
х= Хлев
у= у + 1
while х <= Хправ
Флаг = 0
while (Пиксел (х, у) <> Гран_значение and Пиксел (х, у) <> Нов_значение and х < Хправ if Флаг = 0 then Флаг = 1
x = x + 1
/извлекаем пиксел из стека и присваиваем ему новое значение
/сохраняем x-координату затравочного пиксела
/заполняем интервал справа от затравки
/сохраняем крайний справа пиксел
/восстанавливаем х-координату затравки
/заполняем интервал слева от затравки
/сохраняем крайний слева пиксел
/восстанавливаем х-координату затравки
/проверим, что строка выше не является ни границей многоугольника, ни ухе полностью заполненной; если это не так, то найти затравку, начиная с левого края подынтервала сканирующей строкивосстанавливаем х- координату затравки
/ищем затравку на строке выше
63 |
|
end while |
|
if Флаг = 1 then |
/ помещаем в стек крайний справа пиксел |
if (x = Хправ and Пиксел (х, у) <> Гран_значение and |
|
Пиксел (х, у) <> Нов_значение) then |
|
Push Пиксел (х, у) |
|
elsePush Пиксел (х — 1, у) |
|
end if |
|
Флаг = 0 |
|
end If |
|
Хвход = х |
/ продолжим проверку, если интервал был |
while ((Пиксел (х, у) = Гран_значение оr |
прерван |
Пиксел (х, у) = Нов_значение) and х < Хправ) |
|
х = х + 1 |
|
end while |
|
if х = Хвход then х = х + 1 |
/ удостоверимся, что координата пиксела |
end while |
увеличена |
эта часть алгоритма совершенно аналогична проверке |
/ проверим, что строка ниже не является ни |
для строки выше, за исключением того, что вместо y = |
границей многоугольника, ни уже полностью |
y + 1 надо подставить y = y — 1 |
заполненной |
end while |
|
finish |
|
Пример 2.4. Построчный алгоритм заполнения с затравкой. Рассмотрим работу алгорит-
ма для гранично-определенной области на рис. 2.16. При инициализации в стек помешается затравочный пиксел, помеченный как Затравка (5,7) на рис. 2.16,а. Первоначально в качестве затравки интервала из стека извлекается этот пиксел. Интервал заполняется справа и слева от затравки. Найденные при этом концы интервала Хправ = 9 и Xлев = 1. Затем проверяется строка, расположенная выше текущей и оказывается, что она не граничная и не заполненная. Крайним правым пикселом в диапазоне 1 <= x <= 9 оказывается пиксел (8,8), помеченный цифрой 1 на рис. 2.16,а. Этот пиксел помещается в стек. Затем аналогичным образом обраба-
тывается строка ниже текущей. В диапазоне Хлев <= x <= Xправ есть два подинтервала на этой стороне. Для левого интервала в качестве затравки выступает пиксел (3,6), помеченный циф-
рой 2 на рис. 2.16,а, он тоже помещается в стек. Затравка для правого подинтервала - пиксел (9,6), он помещается в стек. Заметим, что пиксел (9,6) - не самый крайний правый пиксел на интервале, однако это самый крайний правый пиксел в диапазоне Хлев <= x <= Xправ, т.е. в диапазоне 1 <= x <= 9. На этом завершается первый проход алгоритма.

64
Далее из стека извлекается верхний пиксел. Здесь заполняются интервалы, расположенные в правой части многоугольника на последовательных сканирующих строках (рис. 2.16, b, c, d). Для строки 3 затравкой служит пиксел (10,3) (рис. 2.16, d). В результате заполнения интервала справа и слева от затравки получаем новые пределы диапазона Хправ = 10 и Xлев = 1. Обрабатывая строку выше, получаем для основного подынтервала затравочный пиксел (3,4), коорый помещается в стек. Правый подинтервал к этому времени уже заполнен. Обработка строки ниже дает затравку (3,2) для левого и (10,2) для правого подынтервалов. Эти пикселы также помещаются в стек. Именно сейчас достигается максимальная глубина стека для обрабатываемого многоугольника.

65
Теперь остается только один интересный момент. После заполнения 4-связных полигональных подобластей с затравочными пикселами 5, 4 и 3 на рис. 2.16,е из стека извлекается пиксел, помеченный цифрой 2. Здесь мы обнаруживаем, что все пикселы на этой строке уже и на соседних строках (выше и ниже) уже заполнены. Таким образом, ни один пиксел в стек не помещается. Из стека извлекается пиксел 1 и строка обрабатывается, при этом вновь добавочных пикселов не появляется. Теперь стек пуст, многоугольник заполнен и работа алгоритма завершена.
По сравнению с алгоритмом из разд. 2.7 максимальная глубина стека в этом примере равна пяти.
Лабораторные основы
Цель работы: изучить рекурсивный алгоритм закраски произвольно нарисованной области.
Основные понятия, используемые в лабораторной работе: Закраска объектов и областей. Рекурсия. 4-х связные и 8-и связные области.
Рекурсией в программировании называется вызов функции из тела самой функции. Таким образом, рекурсивная функция – это функция, вызывающая сама себя. Пример рекурсивной функции вычисления факториала числа.
Private … Factorial …
If N=1 Then Factorial=1
If N>1 Then Factorial = N*Factorial(N-1) End …
При решении задач закраски выделяют четырёхсвязные и восьмисвязные области.
+y
-x

 +x
+x
-y
x, y+1 |
x-1, y+1 |
x+1, y+1 |
|
x-1, y 

 x+1, y
x+1, y
x-1, y-1 |
x+1, y-1 |
x, y-1
