
- •Понятие электрической цепи. Пассивные и активные элементы линейных электрических цепей.
- •2. Структура электрических цепей постоянного и переменного тока. Законы Ома и Кирхгофа.
- •3. Формы представления синусоидальных токов и напряжений. Метод комплексных амплитуд.
- •4. Расчет линейных электрических цепей с помощью уравнений Кирхгофа.
- •5. Типовые соединения элементов. Расчёт цепей методом эквивалентных преобразований.
- •6. Принцип суперпозиции для линейных электрических цепей. Расчет цепей методом наложения.
- •7. Расчет линейных электрических цепей методом эквивалентного генератора напряжения.
- •8. Электрические цепи трехфазного синусоидального тока.
- •9. Переходные процессы в rc и rl и rlc цепях.
- •10. Мощности и энергетические режимы электрических цепей постоянного и переменного синусоидального тока.
- •11. Понятие четырехполюсника. Системы уравнений и параметры четырехполюсника.
- •12. Определение отклика четырехполюсника на произвольное
- •13. Определение отклика четырехполюсника на произвольное воздействие с помощь переходной и импульсной функций.
- •14. Основные виды пассивных электрических фильтров. Типовые lc- и rc-звенья пассивных фильтров.
- •15. Вынужденные колебания в последовательном колебательном контуре.
- •16. Вынужденные колебания в параллельном колебательном контуре.
- •17. Электрические цепи с распределенными параметрами. Режимы работы и применение длинных линий и волноводов.
- •18. Основные типы антенн и их характеристики.
- •19. Электровакуумные приборы и газоразрядные приборы.
- •20. Электрофизические свойства полупроводниковых материалов. Полупроводниковые резисторы.
- •21. Свойства p-n-перехода. Диоды, их характеристики, условные обозначения и применение.
- •22. Биполярные транзисторы: схемы включения принцип действия в активном режиме.
- •23. Статические характеристики и параметры биполярных транзисторов, линейные схемы замещения.
- •24. Полевые транзисторы с управляющим p-n-переходом и с изолированным затвором. Принцип работы.
- •25. Статические характеристики и параметры полевых транзисторов, линейные схемы замещения.
- •26. Тиристоры: устройство, принцип работы, вольтамперные характеристики, применение.
- •27. Оптоэлектронные приборы.
- •28. Понятие интегральной микросхемы. Условное графическое обозначение и виды микросхем.
- •29. Диэлектрические и магнитные приборы.
- •30. Квантовые и оптические приборы.
- •31. Электронный усилитель. Классификация, характеристики и параметры усилительных устройств.
- •Р ис. 4. Амплитудная характеристика усилителя
- •Р ис. 5. Частотная характеристика усилителя
- •32. Энергетические режимы работы усилительного каскада. Отрицательная обратная связь в усилителях.
- •33. Апериодические и резонансные усилители.
- •34. Автогенераторы гармонических колебаний.
- •35. Устройства преобразования спектра сигналов.
- •36. Импульсные устройства.
- •37. Цифровые и аналого-дискретные устройства.
- •38. Электротехнические устройства: источники электропитания, электрические машины.
- •39. Элементы и устройства автоматики: коммутационные устройства, измерительные преобразователи.
- •40. Электронные системы.
15. Вынужденные колебания в последовательном колебательном контуре.
Последовательный
колебательный контур (рис.
1) содержит конденсатор емкостью C и
катушку индуктивностью L и
сопротивлением R.
Пусть в момент времени t =
0 на конденсаторе имеется заряд ![]() .
При разрядке конденсатора через катушку
возникнет ток и на основе второго закона
Кирхгофа
.
При разрядке конденсатора через катушку
возникнет ток и на основе второго закона
Кирхгофа
|
(1) |
Учитывая,
что ![]() уравнение
(1) может быть преобразовано к виду
уравнение
(1) может быть преобразовано к виду
|
(2) |
где
|
(3) |
(a - коэффициент затухания, w0 – собственная частота контура).
Если  ,
решение уравнения (2)может быть записано
в виде:
,
решение уравнения (2)может быть записано
в виде:
|
(4) |
где ![]()
![]() .
.
Таким
образом, при ![]() зависимость
заряда на конденсаторе от времени имеет
характер затухающих колебаний, частота
которых w,
называемая частотой
свободных колебаний,
несколько меньше собственной частоты
контура w0.
Постоянные qm и j зависят
от начальных условий. В рассматриваемом
случае можно считать w»w0 и j»0;
тогда (4) принимает вид:
зависимость
заряда на конденсаторе от времени имеет
характер затухающих колебаний, частота
которых w,
называемая частотой
свободных колебаний,
несколько меньше собственной частоты
контура w0.
Постоянные qm и j зависят
от начальных условий. В рассматриваемом
случае можно считать w»w0 и j»0;
тогда (4) принимает вид:
. |
(5) |
Закон
изменения силы тока можно найти,
дифференцируя (5) по времени с учетом,
что ![]() .
Тогда
.
Тогда
|
(6) |
Уравнение (6) дает следующее соотношение между амплитудами тока и напряжения:
 ,
,
где
|
(7) |
волновое или характеристическое сопротивлением контура и является одной из его основных характеристик, так как активное сопротивление контура не влияет на соотношение между Um и Im; оно определяет лишь степень затухания колебаний, т.е. быстроту уменьшения амплитуд с течением времени.
Кроме коэффициента затухания a для характеристики затухающих колебаний пользуются логарифмическим декрементом затухания, который равен натуральному логарифму отношения амплитуд колебаний, взятых через период Т:
|
(8) |
Важным параметром колебательного контура является добротность Q, характеризующая относительную убыль энергии в процессе колебаний:
|
(9) |
Энергия
теряемая в контуре за один период,
согласно закону Джоуля – Ленца, равна ![]() ,
где I –
эффективное значение переменного тока.
Энергия, запасенная колебательной
системой, равна максимальной энергии,
накопленной конденсатором или катушкой
индуктивности:
,
где I –
эффективное значение переменного тока.
Энергия, запасенная колебательной
системой, равна максимальной энергии,
накопленной конденсатором или катушкой
индуктивности: 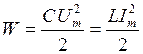 .
Подставляя в (9) выражения для W и WТ,
получим:
.
Подставляя в (9) выражения для W и WТ,
получим:
|
(10) |
16. Вынужденные колебания в параллельном колебательном контуре.
Пусть контур подключен к источнику внешней гармонической ЭДС с амплитудой Еm:
![]() .
.
В соответствии с законом Кирхгофа получаем:
|
(11) |
Решение уравнения (9) можно получить в виде:
|
(12) |
Таким образом, при воздействии на контур периодической ЭДС колебательный процесс в нем вначале представляет собой суперпозицию свободных и вынужденных колебаний. Так как свободные колебания имеют затухающий характер, по истечении некоторого времени ими можно пренебречь и считать, что в контуре существуют лишь вынужденные колебания. Чем выше добротность контура, тем медленнее затухают свободные колебания.
Резонансом в последовательном контуре называется такое явление, при котором резко возрастает амплитуда вынужденных колебаний силы тока, реактивная составляющая входного сопротивления контура равна нулю и контур представляет для генератора чисто активную нагрузку. Резонанс в последовательном колебательном контуре называют резонансом напряжений.
Из этого вытекают следующие свойства резонанса в последовательном контуре:
1. При
резонансе реактивное
сопротивление  ,
поэтому частота генератора
,
поэтому частота генератора
|
(13) |
но
,
т.е. резонанс в последовательном контуре
происходит при частоте генератора wр равной
собственной частоте контура w0.
Строго говоря, это не всегда правильно,
так как при наличии в контуре
сопротивления R собственная
частота его w0 отличается,
хотя и весьма незначительно, от ![]() .
.
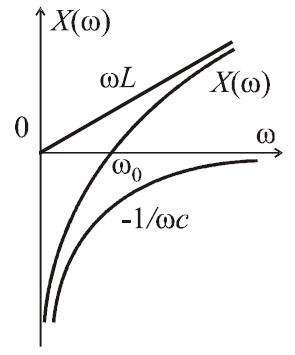
Рис. 2
Характер изменения реактивных сопротивлений катушки индуктивности XL, емкости ХС и контура в целом Х от частоты показан на рис. 2. Следует иметь в виду, что на частотах ниже резонансной сопротивление контура носит емкостной характер, а на частотах выше резонансной – индуктивный.
2.
Равенство
,
при условии. что wр =
w0= ![]() ,
дает
,
дает
|
(14) |
Таким образом, при резонансе индуктивное и емкостное сопротивления контура порознь равны его характеристическому сопротивлению.
Так как при резонансе Х = 0, то полное сопротивление контура:
![]()
Отсюда следует, что между амплитудными значениями ЭДС Еm и тока Imp существует зависимость:
|
(15) |
3. При резонансе ток и ЭДС генератора совпадают по фазе.
4. По
формулам (14) и (15) устанавливаем соотношения
между резонансными амплитудами напряжений
на индуктивности ![]() ,
емкости
,
емкости ![]() и
ЭДС генератора
и
ЭДС генератора ![]() :
:
![]() ,
, 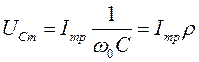 ,
, ![]() ,
,
|
(16) |
Из
выражения (16) следует, что при резонансе
в последовательном контуре амплитуды
напряжения на индуктивности и емкости
равны между собой и каждая из них
превышает амплитуду ЭДС генератора
в Q раз.
Вследствие наличия активного сопротивления
в контуре максимум значений ![]() ,
, ![]() и
и ![]() достигается
при несколько различных значениях
частот. И чем выше добротность контура,
тем ближе эти значения.
достигается
при несколько различных значениях
частот. И чем выше добротность контура,
тем ближе эти значения.
Определим зависимость тока в контуре от частоты в относительном масштабе:
|
(17) |
В
случае использования контура в качестве
фильтрующего элемента имеет смысл
анализировать поведение тока в нем при
относительно небольших отклонениях
частоты сигнала от резонансной. С учетом
этого можно принять, что ![]() .
Если отклонение частоты от резонансной
(расстройку)
обозначить через
.
Если отклонение частоты от резонансной
(расстройку)
обозначить через ![]() то
(17) примет вид
то
(17) примет вид
|
(18) |
Это
соотношение является аналитическим
описанием резонансной, или
амплитудно-частотной, характеристики
контура. Из него видно, что значительные
токи в контуре возникают лишь при
небольших ![]() ,
а следовательно, контур обладает
фильтрующими (избирательными) свойствами.
Избирательные свойства контура, т.е.
способность ослаблять сигналы, частота
которых отличается от резонансной,
характеризуются полосой пропускания.
,
а следовательно, контур обладает
фильтрующими (избирательными) свойствами.
Избирательные свойства контура, т.е.
способность ослаблять сигналы, частота
которых отличается от резонансной,
характеризуются полосой пропускания.
Полосой
пропускания контура ΔF или
ΔΩ (ΔΩ = 2π ΔF)
называется область частот вблизи
резонансной, на границах которой
отношение токов (или напряжений)  .
.
Из соотношения (18) можно получить связь между полосой пропускания, резонансной частотой и добротностью:
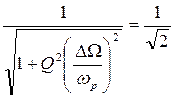 ,
,
откуда легко найти, что
|
(19) |
Ряд нормированных амплитудно-частотных характеристик контуров, отличающихся только добротностью Q, показан на рис. 3.
 Рис.
3
Рис.
3
Фазочастотной характеристикой (ФЧХ) называют зависимость фазового сдвига j тока в контуре относительно вызывающей его ЭДС от частоты. Для последовательного контура имеем


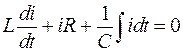
 ,
,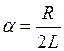 ,
,  ,
,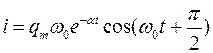 .
.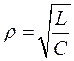
 .
.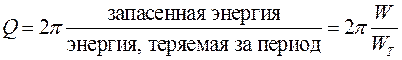 .
.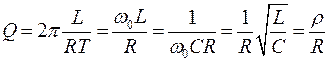 .
.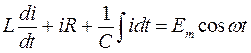 ,
,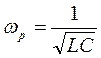 ;
;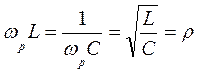 .
.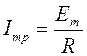 .
.
 .
. .
.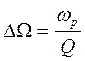 или
или 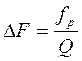 .
.