Общая схема построения интегралов. Теория поля Контрольная работа 9

Задание I. Изменить порядок интегрирования в двойном интеграле. Сделать чертеж области интегрирования.

С. .

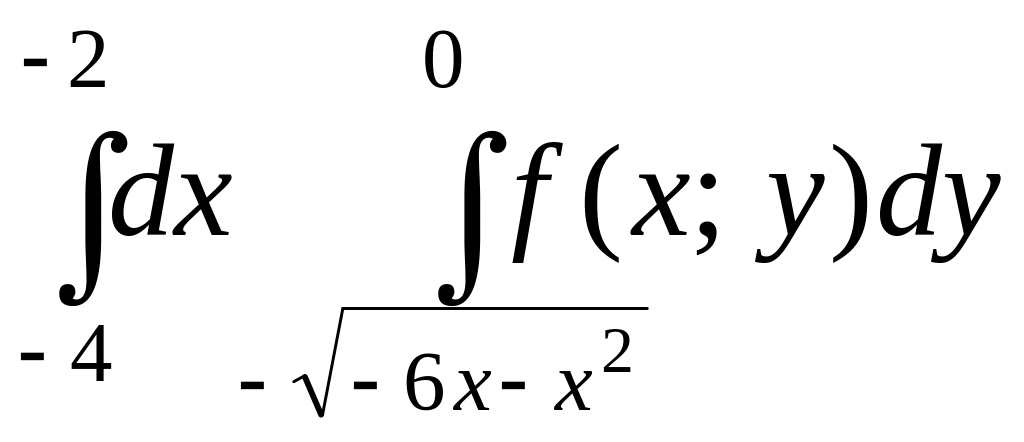Решение.

Из заданного интеграла имеем границы:

,

.

Построим область на графике, выполняя преобразования над уравнениями.

;

;

;

;

.

В результате преобразований получили уравнение окружности, с центром в точке и радиусом 3. Тогда уравнение задает часть этой окружности, расположенной ниже оси .

Построим область интегрирования.

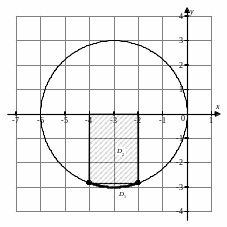
Для того чтобы изменить порядок интегрирования заштрихованную область следует разбить на две области и . Расставим пределы интегрирования по области . Здесь из уравнения или необходимо выразить переменную .

;

;

;

.

Вычислим значение переменной при и :

;

.

Тогда имеем пределы интегрирования по области :

.

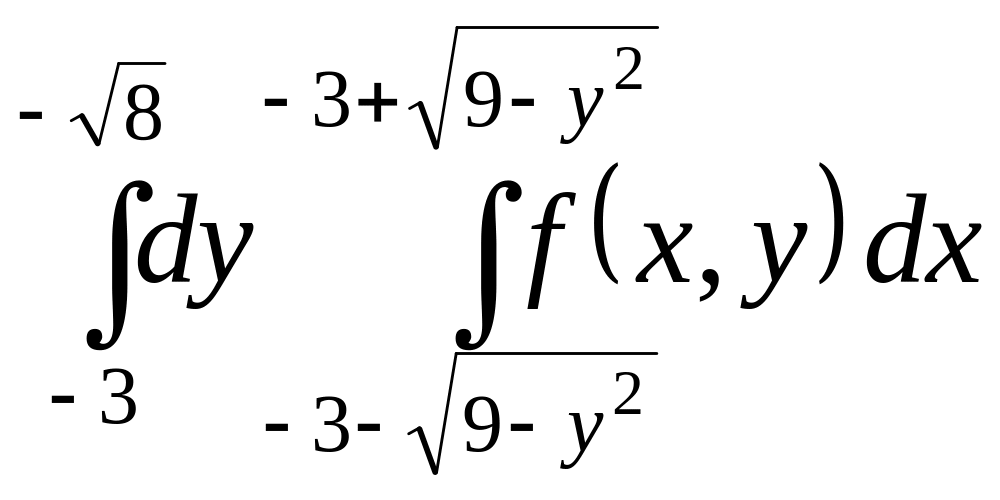Расставим пределы интегрирования по области . Эта область представляет собой прямоугольник: , . Тогда имеем пределы интегрирования по области :

.

Следовательно, объединим

.

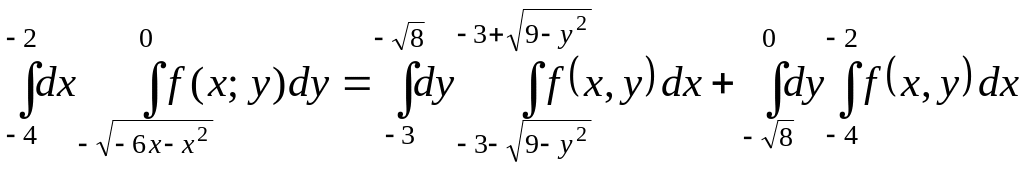Задание II. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекцию на плоскость .

С. .

Решение.

Тело расположено над плоскостью между плоскостями и , снизу ограничено плоскостью : , сверху ограничено параболическим цилиндром .

Объем тела между параболическим цилиндром и плоскостью вычислим по формуле

.

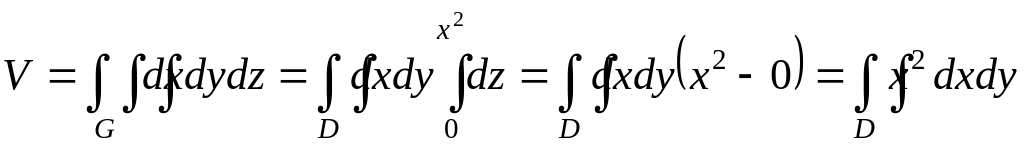Для дальнейших вычислений надо найти область – проекцию на плоскость пространственной области . Для этого решим систему:

 

Построим проекцию на плоскость :

Таким образом, получаем, что параболический цилиндр и плоскость пересекаются при . Следовательно, область – это часть плоскости : , . Таким образом,

 ед³.

Ответ: ед³.

Задание III. Вычислить криволинейный интеграл

С. , где L  ломаная линия, состоящая из отрезков прямых и , от точки до точки .

Решение.

Криволинейный интеграл сводится к вычислению определенного интеграла по формуле:

.

В данном случае имеем для отрезка : , , . Записываем и вычисляем интеграл:

.

Для отрезка : , , . Записываем и вычисляем интеграл:

.

Тогда весь криволинейный интеграл по ломаной от точки до точки :

.

Ответ: .

Задание IV. Требуется:

1) найти поток векторного поля

через замкнутую поверхность (выбирается внешняя нормаль к S);

2) вычислить циркуляцию векторного поля a по контуру , образованному пересечением поверхностей и (направление обхода должно быть выбрано так, чтобы область, ограниченная контуром , находилась слева);

3) проверить правильность вычисленных значений потока и циркуляции с помощью формул Остроградского и Стокса;

4) дать заключение о наличии источников или стоков внутри области, ограниченной поверхностью S;

5) сделать схематический чертеж поверхности S.

Решение.

Строим данные поверхности.

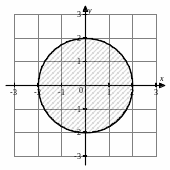
– параболоид вращения с вершиной в точке , ограничен сверху плоскостью , которая проходит параллельно плоскости .

1) Вычислим поток векторного поля через замкнутую поверхность непосредственно, разбивая замкнутую поверхность на гладкие куски поверхности, ограничивающие эту поверхность: , т.е.

Вычислим поток векторного поля с помощью поверхностного интеграла II рода

.

Для вычисления полученного интеграла изобразим на чертеже поверхность и ее проекции на плоскость .

Нормаль к поверхности : образует острый угол с осью (это видно из чертежа). Поэтому при сведении поверхностного интеграла к двойному по области перед двойным интегралом необходимо поставить знак «плюс». Нормалью к поверхности : служит вектор . Тогда поток запишется:

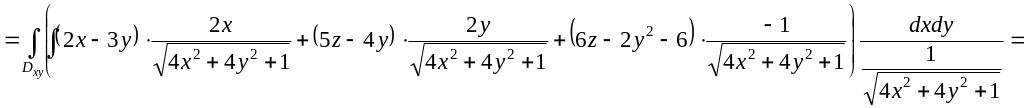
Перейдем к полярным координатам:

.

Вычислим поток векторного поля с помощью поверхностного интеграла II рода через часть поверхности : .

Нормаль к плоскости образует угол в с осью : . Поэтому при сведении поверхностного интеграла к двойному по области перед двойным интегралом необходимо поставить знак «плюс»:

Перейдем к полярным координатам:

.

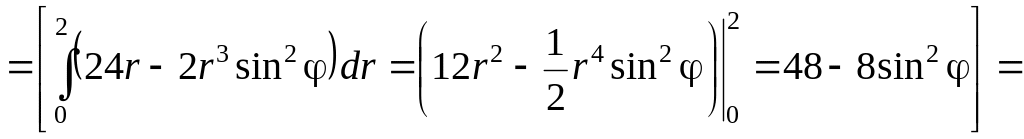
Тогда поток через всю поверхность будет:

.

2) Вычислим циркуляцию векторного поля по замкнутому контуру . Циркуляция поля вдоль контура будет равна:

.

Контуром является окружность, образующаяся при пересечении параболоида с плоскостью .

Запишем параметрические уравнения этой окружности:

,

,

.

При изменении параметра от 0 до получаем требуемое направление обхода контура . Вычислим теперь циркуляцию:

.

3) Вычислим поток векторного поля через замкнутую поверхность пирамиды с помощью теоремы Остроградского-Гаусса.

Вычислим дивергенцию поля :

.

Воспользовавшись формулой Остроградского-Гаусса и переходом к цилиндрическим координатам, вычислим поток векторного поля:

;

.

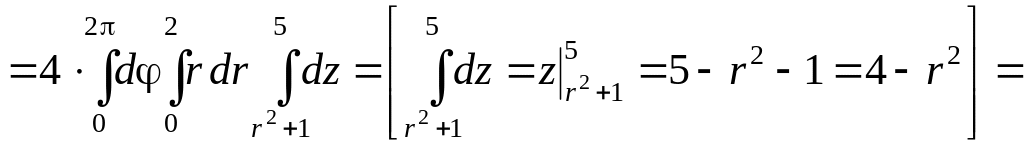
Вычислим циркуляцию, применив формулу Стокса. В качестве поверхности , ограниченной контуром , выступает часть плоскости , ограниченная параболоидом . Единичной нормалью будет вектор . Учитывая поле , по формуле Стокса имеем:

.

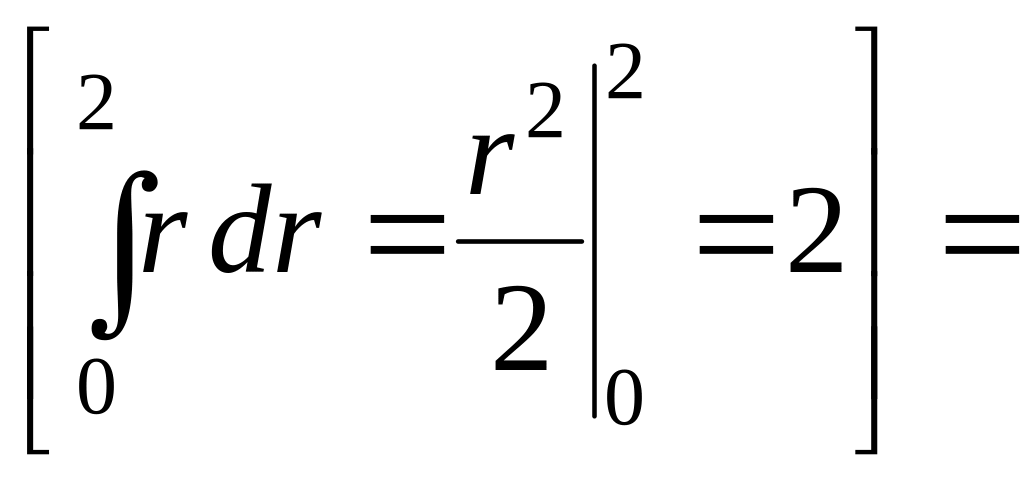
4) Выше была вычислена дивергенция векторного поля

.

Так как она положительна, то все точки являются источниками.

5) Схематический чертеж поверхности :