
Otvety_na_ekzamen_po_matematicheskomu_analizu
.docxМатематический анализ
ИнЭИ (ИЭ–61,62,63,65,66)
1 семестр 2022/2023 уч. год
ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА
1. Предел функции в точке. Свойства пределов.
Пусть
ф-я f(x) определена в некоторой окр-ти
точки x0 за исключением самой быть может
x0. Опр. Число A называется пределом ф-и
f(x) в точке x0, при x→x0, если для любых ∀
ε >0 существует δ(ε) >0 такое что для
любых x из условия модуль разности
модулей x и x0 больше δ выполняется
неравенство: ∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ |f(x)-А|< ε.
 .
0
.
0 |f(x)-А|< ε; - ε <f(x)-А< ε; А-ε<f(x)<A+ε,
бесконечно малая величина.
|f(x)-А|< ε; - ε <f(x)-А< ε; А-ε<f(x)<A+ε,
бесконечно малая величина.
Свойства:
1°
Если
существует предел и он конечен, при
x→x0, то в некоторой окр-ти точки x0 ф-я
f(x0) – ограничена. Док-во: ∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ ⇒
|f(x)-А|< ε. Пусть ε =1, тогда предел
|f(x)-А|<1 по св-ву модулей будет равняться
|f(x)|<1+А. Выполняется для всех x из окр-ти,
принадлежащей ∀x∈Uδ(x0).
Это означает, что ф-я ограничена в
указанной окр-ти. 2°
Если
 существует проколотая окр-ть точки x0
(∃U
δ(x0):) в которой для всех x f(x)>0 ∃U
δ(x0): ∀x
⇒
(x)< 0. 3° Если в некоторой проколотой
окр-ти точка x0
выполняется неравенство f(x)
⩽ f(φ)
или f(x)<
f(φ),
то
существует проколотая окр-ть точки x0
(∃U
δ(x0):) в которой для всех x f(x)>0 ∃U
δ(x0): ∀x
⇒
(x)< 0. 3° Если в некоторой проколотой
окр-ти точка x0
выполняется неравенство f(x)
⩽ f(φ)
или f(x)<
f(φ),
то
 .
4° Лемма 2 милиционера (2м). Если в некоторой
проколотой окр-ти точки x0
выполняются неравенства f(x)⩽g(x)
⩽h(x)
и при этом
.
4° Лемма 2 милиционера (2м). Если в некоторой
проколотой окр-ти точки x0
выполняются неравенства f(x)⩽g(x)
⩽h(x)
и при этом
 .
.
 ,
то
,
то
 .
5° Если
.
5° Если
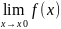 существует, конечен и равняется A,
то ф-ю f(x)
можно записать в следующем виде: f(x)=A+
α(x),
существует, конечен и равняется A,
то ф-ю f(x)
можно записать в следующем виде: f(x)=A+
α(x),
 .
б.м.ф. Док-во: необходимость:
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ1⇒|α(x)|<
ε.
Обозначим разность f(x)
– A
= α(x),
то |α(x)|
< ε
– это определение б.м.ф. ⇒
f(x)
– б.м.ф, при x→x0.
Достаточность:
α(x)
= f(x)
– А, то
и выполняется неравенство |α(x)|
< ε.
Тогда для любых х из проколотой окр-ти
точки (∀x∈Uδ(x0)),
выполняется неравенство |α(x)|
< ε,
а это значит, что у нас есть
.
6° Если существует конечные пределы
.
.
б.м.ф. Док-во: необходимость:
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ1⇒|α(x)|<
ε.
Обозначим разность f(x)
– A
= α(x),
то |α(x)|
< ε
– это определение б.м.ф. ⇒
f(x)
– б.м.ф, при x→x0.
Достаточность:
α(x)
= f(x)
– А, то
и выполняется неравенство |α(x)|
< ε.
Тогда для любых х из проколотой окр-ти
точки (∀x∈Uδ(x0)),
выполняется неравенство |α(x)|
< ε,
а это значит, что у нас есть
.
6° Если существует конечные пределы
.
 ,
то имеют место следующее неравенства:
1)
,
то имеют место следующее неравенства:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ,
при
,
при
 ≠0.
Док-ть
самостоятельно.
7°
≠0.
Док-ть
самостоятельно.
7°
 ,
С = const.
8° Если
существует и конечен, то он единственен.
Док-во: Предположим, что у ф-и 2 разных
предела
,
,
С = const.
8° Если
существует и конечен, то он единственен.
Док-во: Предположим, что у ф-и 2 разных
предела
,
 ,
A≠B,
то ф-ю представим в виде: f(x)=А+
α(x),
x
→ x0;
f(x)=B+
β(x),
x
→ x0.
A
+ α(x)
= B
+ β(x).
A
– B
= β(x)
– α(x).
Мы пришли к противоречию ⇒
A
= B.
,
A≠B,
то ф-ю представим в виде: f(x)=А+
α(x),
x
→ x0;
f(x)=B+
β(x),
x
→ x0.
A
+ α(x)
= B
+ β(x).
A
– B
= β(x)
– α(x).
Мы пришли к противоречию ⇒
A
= B.
2.
Бесконечно малые функции. Сравнение
бесконечно малых функций. Эквивалентные
бесконечно малые функции.
Ф-я f(x)
определённая в некоторой проколотой
окр-ти точки x0
называется бесконечно малой ф-ей,
стремящейся к точке x0,
если предел этой ф-и равен 0. Если
 – функция бесконечно малая или |f(x)|
⩽ ε.
Теорема 1. Сумма или разность бесконечно
малых функций есть бесконечно малая
ф-я. Док-во: α(x),
β(x),
x→x0.
,
– функция бесконечно малая или |f(x)|
⩽ ε.
Теорема 1. Сумма или разность бесконечно
малых функций есть бесконечно малая
ф-я. Док-во: α(x),
β(x),
x→x0.
,
 ;
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ1⇒|α(x)|<
ε;
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ2⇒|β(x)|<
ε.
|α(x)+β(x)|;
|α(x)+β(x)|
⩽
|α(x)+β(x)|
⩽ 2ε.
Замечание. Доказанная теорема остаётся
справедливой для любого конечного
набора бесконечно малых ф-й.
Сравнение Б.М.Ф.
Опр. БМФ α(x)
и β(x),
при x→x0 называются сравнимыми, если
существует пределы их отношения ∃предел
функции α(x)
/ β(x)
по основанию x→x0. Опр. Если
;
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ1⇒|α(x)|<
ε;
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ2⇒|β(x)|<
ε.
|α(x)+β(x)|;
|α(x)+β(x)|
⩽
|α(x)+β(x)|
⩽ 2ε.
Замечание. Доказанная теорема остаётся
справедливой для любого конечного
набора бесконечно малых ф-й.
Сравнение Б.М.Ф.
Опр. БМФ α(x)
и β(x),
при x→x0 называются сравнимыми, если
существует пределы их отношения ∃предел
функции α(x)
/ β(x)
по основанию x→x0. Опр. Если
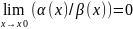 ,
то ф-ю α(x)
называют бесконечно-малая ф-я более
высокого порядка, а бетта(x)
– бесконечно малой более низкого
порядка. Опр. Если
,
то ф-ю α(x)
называют бесконечно-малая ф-я более
высокого порядка, а бетта(x)
– бесконечно малой более низкого
порядка. Опр. Если
 ,
то ф-ю α(x)
называют бесконечно малой более низкого
порядка малости. Опр. Если
,
то ф-ю α(x)
называют бесконечно малой более низкого
порядка малости. Опр. Если
 ,
причём 0<|C|<∞,
то ф-я α(x)
называется бесконечно малого порядка
k
по сравнению с β(x).
Эквивалентные Б.М.Ф. Опр. Бесконечно
малые функции α(x)
/ β(x),
при x→x0, называются эквивалентными,
если
,
причём 0<|C|<∞,
то ф-я α(x)
называется бесконечно малого порядка
k
по сравнению с β(x).
Эквивалентные Б.М.Ф. Опр. Бесконечно
малые функции α(x)
/ β(x),
при x→x0, называются эквивалентными,
если
 .
Таблица эквивалентно
б.м.ф:
.
Таблица эквивалентно
б.м.ф:
![]()
3.
Односторонние пределы.
Опр. Число А называется правосторонним
пределом ф-и f(x) в точке x0
при x→x0+0, если ∀
ε >0 ∃
δ(ε) >0: ∀
x: x0 < x< x0+ δ выполняется неравенство.
Аналогично. Опр. Число В называется
левосторонним пределом ф-и f(x) в точке
x0,
при x→x0-0, если ∀
ε >0 ∃
δ(ε) >0: ∀
x:0<|x-x0|<δ ⇒
|f(x)-А|< ε. Теорема. Для того, чтобы для
ф-и f(x), x→x0 существовал двухсторонний
предел Н и Д (необходимо и достаточно),
чтобы существовали конечные односторонние
пределы и были равны между собой:
 .
.
4.
Бесконечно большие функции и их свойства.
Опр. Пусть ф-я
f(x) определена в некоторой проколотой
окр-ти т. x0,
модуля ф-и, при x→x0 = ∞, если для любых
М>0 такое, что для любых x
∀
ε >0 ∃
δ(ε) >0: ∀
x:0< |x-x0|< δ ⇒
|f(x)-А|>M.
 f(x). Замечание. Иногда приходится различать
положительные ББФ от отрицательных,
т.е. рассматривать не двухсторонний
предел, а односторонние пределы.
f(x). Замечание. Иногда приходится различать
положительные ББФ от отрицательных,
т.е. рассматривать не двухсторонний
предел, а односторонние пределы.
Свойства ББФ: 1° Сумма ББФ одного знака и любого их конечного числа есть ББМ, при x→x0. 2° Если f(x) – ББФ, при x→x0, то 1/ f(x) – ББФ, при x→x0. 3° Если f(x) – ББФ, при x→x0, а φ(x) – ограниченная ф-я в некоторой окр-ти точки x0 и не обращается в 0, то φ(x)* f(x) – Б.Б.Ф., при x→x0.
5.
Непрерывность функции в точке.
Классификация точек разрыва. Пусть
ф-я f(x) определена в некоторой окр-ти
точки x0,
включая саму точку x0.
Опр. Функция f(x) называется непрерывной
в точке x0,
если
 f(x) (1). ∀
ε >0 ∃
δ(ε) >0, ∀
x:0 < |x-x0|< δ(M)
⇒
|f(x)-f(x0)|<
ε. x
– x0
= Δx,
y
– y0
= Δy
– приращение ф-и.
f(x) (1). ∀
ε >0 ∃
δ(ε) >0, ∀
x:0 < |x-x0|< δ(M)
⇒
|f(x)-f(x0)|<
ε. x
– x0
= Δx,
y
– y0
= Δy
– приращение ф-и.
 (2) Опр. f(x)
называется непрерывной в точке x0,
если выполняется равенство (2). Опр. f(x)
называется непрерывной (a;
b),
если она непрерывна в каждой точке этого
интервала. Опр. Если f(x)
не является непрерывной в точке x0,
то она называется разрывной ф-ей, а точка
x0
называется точкой разрыва. Опр. ф-я f(x)
называется непрерывной в точке x0,
если предел слева равен пределу справа
и равен f(x).
(2) Опр. f(x)
называется непрерывной в точке x0,
если выполняется равенство (2). Опр. f(x)
называется непрерывной (a;
b),
если она непрерывна в каждой точке этого
интервала. Опр. Если f(x)
не является непрерывной в точке x0,
то она называется разрывной ф-ей, а точка
x0
называется точкой разрыва. Опр. ф-я f(x)
называется непрерывной в точке x0,
если предел слева равен пределу справа
и равен f(x).
 (3). Классификация точек разрыва. Опр.
Точка x0
называется точкой устранимого разрыва
ф-и f(x), если выполняется неравенство:
(3). Классификация точек разрыва. Опр.
Точка x0
называется точкой устранимого разрыва
ф-и f(x), если выполняется неравенство:
 ;
f(x)
= sinx/x,
x≠0;
;
f(x)
= sinx/x,
x≠0;
 .
x
= 0 – устранимая точка разрыва. Опр. Точка
x0 называется точкой разрыва первого
рода, если существуют конечные
односторонние пределы и они не равны
между собой. ;
.
x
= 0 – устранимая точка разрыва. Опр. Точка
x0 называется точкой разрыва первого
рода, если существуют конечные
односторонние пределы и они не равны
между собой. ;
 f(x).
Опр. Точкой x0
называется точкой разрыва 2 рода, если
односторонние пределы один или оба не
существуют или = ∞.
f(x).
Опр. Точкой x0
называется точкой разрыва 2 рода, если
односторонние пределы один или оба не
существуют или = ∞.
6.
Свойства непрерывных функций на отрезке.
Теорема 1. «Первая теорема Больцано-Коши».
Если f(x) непрерывно на отрезке [a;
b]
и в концах этого отрезка принимает
значение разных знаков, то внутри отрезка
найдётся по крайней мере одна точка. В
которой значение ф-и равно 0. f(С) = 0.
 Теорема 2. «Вторая теорема Больцано-Коши».
Если f(x) непрерывно на отрезке [a;
b]
и если f(a)=A,
f(b)=B,
то значений ф-й f(x) сплошь заполняют
отрезок [A;
B]
это означает, что для произвольной точки
С из интервала [A;
B]
существует точка С из интервала (a;
b).
С∈(A;
B);
С∈(a;
b).
Теорема 2. «Вторая теорема Больцано-Коши».
Если f(x) непрерывно на отрезке [a;
b]
и если f(a)=A,
f(b)=B,
то значений ф-й f(x) сплошь заполняют
отрезок [A;
B]
это означает, что для произвольной точки
С из интервала [A;
B]
существует точка С из интервала (a;
b).
С∈(A;
B);
С∈(a;
b).
7.
Производная функции. Механический и
геометрический смысл производной.
Рассмотрим ф-ю y=f(x),
определённую на некотором интервале
(a;
b),
при а=-∞, а=+∞. Пусть точка x0∈(a;
b), y0=f(x).
![]() x-x0
= Δx – приращение аргумента. f(x)
– f(x0)
= Δf(x0)
= Δy0
– приращение ф-и в точке x0.
x-x0
= Δx – приращение аргумента. f(x)
– f(x0)
= Δf(x0)
= Δy0
– приращение ф-и в точке x0.
 (1). Если существует конечный предел (1),
то он называется производной ф-ей f(x) в
точке x0 и обозначается f '(x0) = y'. Примеры.
Механический смысл производный.
(1). Если существует конечный предел (1),
то он называется производной ф-ей f(x) в
точке x0 и обозначается f '(x0) = y'. Примеры.
Механический смысл производный.
![]() S
– путь, пройденный мат. точкой за время
от момента t0
до момента t0+
Δt.
ΔS
= S(t0
+ Δt)
– S(t0).
Рассмотрим ΔS
на Δt.
Это отношение определяет среднюю
скорость движения точки за время t0.
Опр.
S
– путь, пройденный мат. точкой за время
от момента t0
до момента t0+
Δt.
ΔS
= S(t0
+ Δt)
– S(t0).
Рассмотрим ΔS
на Δt.
Это отношение определяет среднюю
скорость движения точки за время t0.
Опр.
 называется мгновенной скоростью
движения мат. точки в момент времени t.
Геометрический смысл производной.
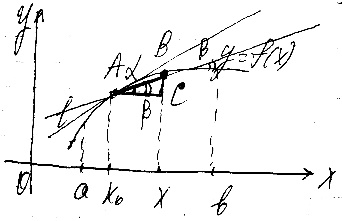
Рассмотрим y=f(x),
определённую на интервале (a;
b)
и проведём секущ. AB,
l
= кас. в точке, AB
– секущая.
называется мгновенной скоростью
движения мат. точки в момент времени t.
Геометрический смысл производной.
Рассмотрим y=f(x),
определённую на интервале (a;
b)
и проведём секущ. AB,
l
= кас. в точке, AB
– секущая.
 .
Геометрический смысл производной
состоит в том, что производная состоит
в том, что производная ф-и в точке = tg
α наклона касательной, проведённой к
данной кривой в соответствующей точке
с положительным направлением оси x.
.
Геометрический смысл производной
состоит в том, что производная состоит
в том, что производная ф-и в точке = tg
α наклона касательной, проведённой к
данной кривой в соответствующей точке
с положительным направлением оси x.
8.
Дифференцируемость функции. Правила
вычисления производной.
Пусть ф-я f(x) на интервале (a;
b) Δy = f(x+x0) - f(x). Теорема: Ф-я f(x) называется
дифференцируемой в т. x,
если её приращение можно представить
в виде Δy=А* Δx+α(Δx)* Δx;
 α(Δx). Док-во. Необходимость. Если f(x)
диф-ма в т. x по условию теоремы, т.е.
выполняется равенство:
α(Δx). Док-во. Необходимость. Если f(x)
диф-ма в т. x по условию теоремы, т.е.
выполняется равенство:
 ,
то при переходе к
,
то при переходе к
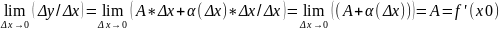 .
Достаточность.
.
Достаточность.
 ⇒ Δy
= f '(x)*Δx + α(Δx)*Δx. Теорема. Если ф-я y=f(x)
диф-ма в т. x,
то она непрерывна в этой точке.
⇒ Δy
= f '(x)*Δx + α(Δx)*Δx. Теорема. Если ф-я y=f(x)
диф-ма в т. x,
то она непрерывна в этой точке.
 .
.
Пусть ф-я f(x) и h(x) диф-мы в точке x, тогда имеют место следующие равенства: 1. (f(x) ± h(x))'=f '(x) ± h'(x); u(x)=f(x)+h(x), тогда u(x+Δx) = f (x+Δx)+h(x+Δx); Δx=f(x+Δx) =f(x) = h(x+Δx) – h(x);
 .
Следствие: если f(x)
диф-мо в т. x,
а С=const,
то производная от произведения С на
ф-ю, т.е. (с*f(x))'=C*f(x).
2. (f(x)*h(x))'=f
'*h+f*h'.
3. (f/h)'=(f
'*h
- f*h')/h^2.
.
Следствие: если f(x)
диф-мо в т. x,
а С=const,
то производная от произведения С на
ф-ю, т.е. (с*f(x))'=C*f(x).
2. (f(x)*h(x))'=f
'*h+f*h'.
3. (f/h)'=(f
'*h
- f*h')/h^2.
9.
Производная сложной функции. Таблица
производных. Пусть
ф-я f(x) диф-ма в т. x,
а ф-я u=h(x)
диф-ма в соответствующей точке y,
тогда u=h(f(x))
диф-ма в т.x
и имеет место равенство: V'
= h'
(f(x))*f
'(x);
Δx → Δy → Δu;
Δu=h'(y)*Δy
+ α(Δy)*Δy;
Δy=
f
'(x)*Δx
+ β(Δx)*Δx,
α и β
– б.м.ф.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
10.
Обратная функция и ее производная. Пусть
ф-я f(x) определена на [a;
b].
Опр. Ф-я f(x) называется взаимно-однозначной
на интервале [a;
b],
если различные точки x1,
x2
из интервала [a;
b]
соответствуют значению ф-и f(x1)
≠ f(x2).
Пусть ф-я y
= f(x) определена, взаимно-однозначно и
непрерывна на интервале [a;
b]
 y∈(f(a);
f(b)) соответствует единственное значение
x∈(a;
b), тем самым интервалам (f(a); f(b)) определена
ф-я α(y), которая яв-ся обратной ф-ей f(x).
График прямой ф-и совпадает с графиком
обратной, если x
= f^-1(y)
= h(y).
x
= siny
обратная ф-я y=arcsinx.
Теорема. Если ф-я y=f(x)
определена, взаимооднозначна и непрерывна
на интервале (a,
b),
то на интервале (f(a); f(b)) существует
обратная ф-я также взаимно-однозначно
и непрерывная y=^-1(x).
Теорема. Пусть ф-я y=f(x)
определена, взаимооднозначна и
дифференцируема на интервале (a;
b),
причём f
'(x) ≠ 0 ⇒ на
соответствующем интервале (f(a);
f(b)) существует обратная ф-я y
= f^-1(x)
также дифференцируемая, причём имеет
место равенство: (f^-1(x))'
= (1/f
'(x)).
Док-во: Фиксируемая точка x∈(a;
b). Стоим приращение Δx.
Составим отношение Δx/Δy=1/(Δy/Δx)
⇒
y∈(f(a);
f(b)) соответствует единственное значение
x∈(a;
b), тем самым интервалам (f(a); f(b)) определена
ф-я α(y), которая яв-ся обратной ф-ей f(x).
График прямой ф-и совпадает с графиком
обратной, если x
= f^-1(y)
= h(y).
x
= siny
обратная ф-я y=arcsinx.
Теорема. Если ф-я y=f(x)
определена, взаимооднозначна и непрерывна
на интервале (a,
b),
то на интервале (f(a); f(b)) существует
обратная ф-я также взаимно-однозначно
и непрерывная y=^-1(x).
Теорема. Пусть ф-я y=f(x)
определена, взаимооднозначна и
дифференцируема на интервале (a;
b),
причём f
'(x) ≠ 0 ⇒ на
соответствующем интервале (f(a);
f(b)) существует обратная ф-я y
= f^-1(x)
также дифференцируемая, причём имеет
место равенство: (f^-1(x))'
= (1/f
'(x)).
Док-во: Фиксируемая точка x∈(a;
b). Стоим приращение Δx.
Составим отношение Δx/Δy=1/(Δy/Δx)
⇒
 ;
y=arcsinx⇒x=siny=Δx/Δy=
h'(y)=1/f
'(x)
= 1/корень из 1-sin^2(y)
= ±1/корень из 1-x.
Если мы рассматриваем cos
на промежутке (π; π/2), тогда перед корнем
стоит знак +. y=arctg⇒x=tgy.
(arctg)'
= (1/(tgx)') = 1/1/cos^2(y) = cos^2(y) = 1/1+tg^2(y) = 1/1+x^2.
Таблица
производных обратных ф-й.
;
y=arcsinx⇒x=siny=Δx/Δy=
h'(y)=1/f
'(x)
= 1/корень из 1-sin^2(y)
= ±1/корень из 1-x.
Если мы рассматриваем cos
на промежутке (π; π/2), тогда перед корнем
стоит знак +. y=arctg⇒x=tgy.
(arctg)'
= (1/(tgx)') = 1/1/cos^2(y) = cos^2(y) = 1/1+tg^2(y) = 1/1+x^2.
Таблица
производных обратных ф-й.
![]()
11. Дифференциал функции первого порядка и его свойства. Геометрический смысл дифференциала. Пусть ф-я y=f(x) определена и диффундирована на интервале (a; b). Рассмотрим т. x∈(a; b); т.к. ф-я дифференцируема, то её приращение можно представить в виде: Δy=А*Δx + Δx*α(Δx), Δx→0. Дифференциалом ф-и f(x) называется главная линейная относительно Δx часть приращения ф-и и обозначается (d/dx)*(x^3 + 2x) = dy = A* Δx; A = f(x); dy = f(x)*Δx. Если x независимая переменная, то Δx=dx, т.е. приращение независимой переменной = дифференциалу этой переменной. dy = f '(x)*dx ⇒ f '(x) = dy/dx. Дифференциал. Символ dy/dx можно рассматривать как дробь, т.е. как отношение двух дифференциалов. Замечание. С одной стороны dx – число, а с другой стороны – б.м.ф.
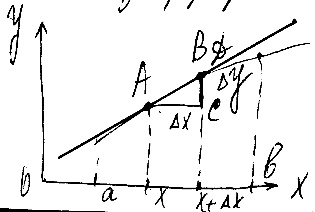 Ординаты что это
приращение ординаты касательной,
проведённой в соответствующий точке
кривой. Если dx
достаточно мало, то Δy
приближённо = dy.
Формула прогноза: f(x
+ Δx)
≈ f(x)
+ f
'(x)*Δx;
Δy=f(x+Δx)
– f(α).
Ординаты что это
приращение ординаты касательной,
проведённой в соответствующий точке
кривой. Если dx
достаточно мало, то Δy
приближённо = dy.
Формула прогноза: f(x
+ Δx)
≈ f(x)
+ f
'(x)*Δx;
Δy=f(x+Δx)
– f(α).
Пусть ф-и u(x) и V(x) диф-мы на интервале (a; b) ⇒ имеют место следующих равенства: du=f '(x)*dx – определение дифференциала. 1) d(u ± V) = du ± dV; 2) d(u*V) = du*V + u*dV; 3) d(u/V) = (du*v + u*dV)/V^2, V≠0. Дик-во: d(u*V) = (u*V)'*dx*V + u*V'*dx = du*V+u*dV.
12. Логарифмическое дифференцирование. Инвариантность формы дифференциала первого порядка. y = u(x)^V(x); lny = lnu(x)^V(x) = V(x)*lnu(x)*(lny)' = (1/y)*y' ⇒ y'=y*(lny) = y(V'*lnu+V*(1/u)*u'). Формула: y = u(x)^V(x) = e^V(x)*lnu(x) = y' = (e^V(x)*lnu(x)) * (V')*lnu + V*(1/u)*u').
Рассмотрим ф-ю y=f(x), дифференцированную на интервале (a; b), где x – независимая переменная ⇒ dy = f '(x)*dx (1); dx = Δx – число. Предположим x = φ(t) на некотором промежутке t∈(α; β). Пусть эта ф-я дифференцируема на этом промежутке ⇒ сложная ф-я y = f(φ(t)) также дифференцируема на интервале (α; β). Найдём дифференциал этой ф-и: dy = (f(φ(t)))'*dt = f '(φ(t))* φ'(t)*dt = f '(x)*dx. (2) Замечание. Форма дифференциала в равенствах (1) и (2) не изменилось, однако смысл dx разный. В (1) dx – число, а в (2) dx – дифференциал ф-и.
13. Производная параметрически заданной функции. Односторонние производные.
Пусть
ф-я y=f(x) задана параметрически. Это
означает, что ф-я задаётся с помощью
системы(1).
 ,
∈(α;
β).
,
∈(α;
β).
 , где r
– радиус окружности.
, где r
– радиус окружности.
Пусть ф-я φ(t) и ψ(t) дифференцирована на интервале (α; β). Ф-я равная φ(t) имеет обратную ф-ю, которая также яв-ся дифференцируемой на соответствующем интервале x. Запишем производную параметрически заданной ф-и. y'x = ψ'(t)/φ'(t). Док-во: 1 способ. dy = f '(x)*dx ⇒ f '(x)=dy/dx; dy/dx = ψ'(t)*dt/φ'(t)*dt = ψ'(t)/φ'(t). Док-во: 2 способ. y = ψ'(φ^-1(x)); y' = ψ'(t)/φ'(t).
Пусть
ф-я y=f(x) задана на отрезке (a;
b).
Предположим, что она дифференцируема
на интервале (a;
b).
Т.е. в каждой точке интервала существует
производная. f
'(x)
=
 .
Обычная производная называется
двухсторонней.
.
Обычная производная называется
двухсторонней.
![]() Производную в точке a
можно писать f
'(a
+ 0) =
Производную в точке a
можно писать f
'(a
+ 0) =
 (1). Производная, найденная по формуле
(1), называется правосторонней, аналогично
f
'(b
- 0) =
(1). Производная, найденная по формуле
(1), называется правосторонней, аналогично
f
'(b
- 0) =
 .
Называется левосторонней. Замечание.
Правосторонняя и левосторонняя
производные ф-и могут быть определены
произвольной точкой отрезка (a;
b).
Т.е. мы можем записать f
'(x
+ 0) =
;
f '(x + 0) =
..
Теорема. Для того чтобы для ф-и y=f(x) в
некоторой точке x существовала
двухсторонняя производная НиД, чтобы
в этой точке в ∃
- ли конечные левосторонние и правосторонние
производные и были равны между собой.
.
Называется левосторонней. Замечание.
Правосторонняя и левосторонняя
производные ф-и могут быть определены
произвольной точкой отрезка (a;
b).
Т.е. мы можем записать f
'(x
+ 0) =
;
f '(x + 0) =
..
Теорема. Для того чтобы для ф-и y=f(x) в
некоторой точке x существовала
двухсторонняя производная НиД, чтобы
в этой точке в ∃
- ли конечные левосторонние и правосторонние
производные и были равны между собой.
14.
Производные и дифференциалы высших
порядков. Формула Лейбница. Пусть
ф-я y'=f '(x) диф-ма в некоторой точке
интервала (a;
b).
Может оказаться, что производная в свою
очередь является дифференцируемой ф-й.
y'' = (f
'(x))'
= f^(2)(x)
= d^2*(y)/d*x^2.
Опр. Производная n-го
порядка от f(x)
= первой производной от производной
(n-1)-ой.
f^(n)(x)
= (f^(n-1)(x))'.
Для существующих f^(n)(x)
необходимо существование (f^(n-1)(x))
в некоторой окр-ти точки x0.
Пусть u(x)
и V(x)
диф-ма n раз на некотором интервале (a;
b) ⇒
производная (u±V)^(n) = u^(n)±V(n). Формула
Лейбница:
![]() n!
= 1*3*3*…*n; 0! = 1. Пусть ф-я y=f(x) на (a; b) ⇒
дифференциал dy = f '(x) = d(x)*dx – первый
дифференциал. Предполагает, что ф-я f(x)
дифференцируема сколько угодно раз.
d(dy) = d^2*(y) = d(f '(x)*dx) = d(f '(x))*dx + f '(x)*d(dx) = f
''(x)*dx^2… d^(n)*y = f^(n)(x)*dx^n.
n!
= 1*3*3*…*n; 0! = 1. Пусть ф-я y=f(x) на (a; b) ⇒
дифференциал dy = f '(x) = d(x)*dx – первый
дифференциал. Предполагает, что ф-я f(x)
дифференцируема сколько угодно раз.
d(dy) = d^2*(y) = d(f '(x)*dx) = d(f '(x))*dx + f '(x)*d(dx) = f
''(x)*dx^2… d^(n)*y = f^(n)(x)*dx^n.
15.
Теорема Ферма и теорема Коши. Ферма.
Если ф-я y=f(x)
диф-ма в точке x0
и эта точка яв-ся точкой экстремума, то
производная ф-и в этой точке равна 0.
Док-во: Предположим, что x0
– точка локального максимума. f(x0
+ Δx) – f(x0) ⩽ 0. Если
Δx>0. ⇒
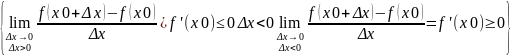 .
Коши. Если ф-я y
= f(x)
и y
= g(x)
удовлетворяют следующим 3-м условиям:
1) Они непрерывны на отрезке [a; b]. 2) Диф-мы
на интервале (a; b). 3. g(x) ≠ 0; g'(x) ≠ 0 на
интервале (a; b) ⇒
на этом интервале существует хотя бы
одна точка с, в котором выполняется
равенство (5). (f(b) – f(a))/(g(b) – g(a)) =f'(c)/g(c) 5
Док-во: Введём вспомогательную ф-ю F(x).
F(x) = f(x) – f(a) – ((f(b) – f(a))/(f(b) – g(x))) * (g(x) –
g(x)) (6). При
f(b)
– g(x)
≠ 0. Док-во проводится аналогично
предыдущей теореме Лагранжа. По условиям
теоремы Ролля существует хотя бы одна
точка с, в которой F'(x)=0 ⇒
получим (5).
.
Коши. Если ф-я y
= f(x)
и y
= g(x)
удовлетворяют следующим 3-м условиям:
1) Они непрерывны на отрезке [a; b]. 2) Диф-мы
на интервале (a; b). 3. g(x) ≠ 0; g'(x) ≠ 0 на
интервале (a; b) ⇒
на этом интервале существует хотя бы
одна точка с, в котором выполняется
равенство (5). (f(b) – f(a))/(g(b) – g(a)) =f'(c)/g(c) 5
Док-во: Введём вспомогательную ф-ю F(x).
F(x) = f(x) – f(a) – ((f(b) – f(a))/(f(b) – g(x))) * (g(x) –
g(x)) (6). При
f(b)
– g(x)
≠ 0. Док-во проводится аналогично
предыдущей теореме Лагранжа. По условиям
теоремы Ролля существует хотя бы одна
точка с, в которой F'(x)=0 ⇒
получим (5).
16.
Теорема Ролля и теорема Лагранжа. Роля.
Если ф-я y=f(x)
удовлетворяет следующим 3-м условиям:
1. Она непрерывна на отрезке [a;
b].
2. Она диф-ма на интервале (a;
b).
3. f(a)
= f(b),
тогда внутри интервала (a;
b)
хотя бы одна точка с, такая что производная
в этой точке = 0. f
'(c)
= 0.
 Лагранжа. Если ф-я y=f(x)
удовлетворяет следующим 2-м условиям:
1. Она непрерывна на отрезке [a;
b].
2. Диф-ма на интервале (a; b) ⇒
на этом интервале существует хотя бы
одна точка с, такая что выполняется
равенство: f(b)-f(a) = f '(c)*(b-a) (3). Док-во: Для
док-ва рассмотрим вспомогательную ф-ю
F(x) = f(x) – f(a)-((f(b)-f(a))/(b-a))*(x-a) (4). Заметим,
что эта ф-я удовлетворяет перечисленным
двум условиям теоремы. Посчитаем значения
ф-и на концах отрезка. F(a) = f(b) – f(a) –
((f(b) – f(a))/(b-a))*(b-a) = 0 ⇒
по теореме Ролля существует хотя бы
одна точка с, в которой F'(c) = 0. Разность
f(b) от
f(a) = F '(x) = f '(x) – (f(b) – f(a))/(b-a).
Лагранжа. Если ф-я y=f(x)
удовлетворяет следующим 2-м условиям:
1. Она непрерывна на отрезке [a;
b].
2. Диф-ма на интервале (a; b) ⇒
на этом интервале существует хотя бы
одна точка с, такая что выполняется
равенство: f(b)-f(a) = f '(c)*(b-a) (3). Док-во: Для
док-ва рассмотрим вспомогательную ф-ю
F(x) = f(x) – f(a)-((f(b)-f(a))/(b-a))*(x-a) (4). Заметим,
что эта ф-я удовлетворяет перечисленным
двум условиям теоремы. Посчитаем значения
ф-и на концах отрезка. F(a) = f(b) – f(a) –
((f(b) – f(a))/(b-a))*(b-a) = 0 ⇒
по теореме Ролля существует хотя бы
одна точка с, в которой F'(c) = 0. Разность
f(b) от
f(a) = F '(x) = f '(x) – (f(b) – f(a))/(b-a).
17. Правило Лопиталя.
Пусть имеется предел отношения двух
ф-й.
 .
Теорема Лопиталя (для неопределённости
{0/0}): пусть ф-и f(x)
и h(x)
на некотором интервале (a;
b)
удовлетворяют следующим условиям: 1.
Они определены на этом интервале за
исключением быть может точки x0.
2. Диф-мы на этом интервале за исключением
точки x0.
.
Теорема Лопиталя (для неопределённости
{0/0}): пусть ф-и f(x)
и h(x)
на некотором интервале (a;
b)
удовлетворяют следующим условиям: 1.
Они определены на этом интервале за
исключением быть может точки x0.
2. Диф-мы на этом интервале за исключением
точки x0.
 ;
;
 ,
если существует
,
если существует
 ,
то существует и предел отношения самих
ф-й, причём имеет место равенство:
,
то существует и предел отношения самих
ф-й, причём имеет место равенство:
 (1). Замечание: если при 1-ом применении
правила Лопиталя снова получайте
неопределённость типа {0/0}, то правило
Лопиталя применяется повторно. Замечание:
Предел в правой части равенства (1) может
не существовать, однако предел в левой
части равенства при этом может
существовать. Теорема Лопиталя для
({∞/∞}). Если ф-я f(x)
и h(x)
определены на интервале (a;
b)
за исключением точки x0
этого интервала и удовлетворяют следующим
условиям: 1. f(x)
и h(x)
непрерывны и диф-мы на интервале (a; b) за
исключением точки x0. 2. Пределы этих ф-й
= ∞. (
;
(1). Замечание: если при 1-ом применении
правила Лопиталя снова получайте
неопределённость типа {0/0}, то правило
Лопиталя применяется повторно. Замечание:
Предел в правой части равенства (1) может
не существовать, однако предел в левой
части равенства при этом может
существовать. Теорема Лопиталя для
({∞/∞}). Если ф-я f(x)
и h(x)
определены на интервале (a;
b)
за исключением точки x0
этого интервала и удовлетворяют следующим
условиям: 1. f(x)
и h(x)
непрерывны и диф-мы на интервале (a; b) за
исключением точки x0. 2. Пределы этих ф-й
= ∞. (
;
 ).
3. h(x) ≠ 0; h'(x) ≠ 0 на интервале (a; b) ⇒
если существует предел отношения ф-й
этих ф-1, то существует предел отношения
самих ф-й и имеет место равенство (1).
).
3. h(x) ≠ 0; h'(x) ≠ 0 на интервале (a; b) ⇒
если существует предел отношения ф-й
этих ф-1, то существует предел отношения
самих ф-й и имеет место равенство (1).
18.
Асимптоты графика функции. Опр.
Прямая x=x0
называется вертикальной асимптотой
для ф-и f(x),
если
 .
Опр. Прямая y
= kx+b
называется наклонной асимптотой для
ф-и f(x),
при x→∞,
если f(x)
можно представить в виде: y
= f(x)
= kx
+ b
+ α(x).
.
Опр. Прямая y
= kx+b
называется наклонной асимптотой для
ф-и f(x),
при x→∞,
если f(x)
можно представить в виде: y
= f(x)
= kx
+ b
+ α(x).
 .
Замечание. Для того, чтобы можно было
говорить о наклонной асимптоте ф-я f(x)
должна быть определена для сколь угодно
больших положительных x
и сколь угодно больших отрицательных
x.
Теорема. Для того, чтобы прямая y
= f(x)
= kx
+ b
была наклонной асимптотой для ф-й y
= f(x)
НиД выполнения следующих равенств. K
=
.
Замечание. Для того, чтобы можно было
говорить о наклонной асимптоте ф-я f(x)
должна быть определена для сколь угодно
больших положительных x
и сколь угодно больших отрицательных
x.
Теорема. Для того, чтобы прямая y
= f(x)
= kx
+ b
была наклонной асимптотой для ф-й y
= f(x)
НиД выполнения следующих равенств. K
=
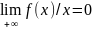 (1). b
=
(1). b
=
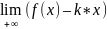 (2). Заметим, что формулами (1) и (2)
определяются коэффициенты k
и b
на положительную ∞, аналогичные формулы
имеют место для x→-∞.
Замечание. Если хотя бы один из пределов
(1) и (2) = ∞ или не существует, то наклонной
асимптоты нет. Если k=0,
то y=b
– горизонтальная асимптота.
(2). Заметим, что формулами (1) и (2)
определяются коэффициенты k
и b
на положительную ∞, аналогичные формулы
имеют место для x→-∞.
Замечание. Если хотя бы один из пределов
(1) и (2) = ∞ или не существует, то наклонной
асимптоты нет. Если k=0,
то y=b
– горизонтальная асимптота.
19.
Условия возрастания и убывания
дифференцируемой на интервале функции.
Пусть ф-я y=f(x)
определена и непрерывна на некотором
интервале (a;
b).
Опр. Ф-я y=f(x) называется неубывающей на
отрезке (a;
b),
если для любых x1,
x2
из отрезка (a;
b)
таких что a
<= x1
< x2
<= b
имеет место следующее неравенство: f
(x1)
<= f
(x2).
Если же f
(x1)
< f
(x2),
то й-я называется возрастающей. Опр. Ф-я
y=f(x) называется невозрастающей на отрезке
(a;
b).
Если для любых f1,
x2
из отрезка (a;
b)
для которых выполняется неравенство a
<= x1
< x2
<= b
имеет место следующее неравенство: f
(x1)
> f
(x2),
то ф-я называется убывающей. Опр. Ф-я не
убывающая или не возрастающая на
некотором промежутке называется
монотонной. Опр. Ф-я возрастающая или
убывающая на некотором промежутке
называется строго монотонной. Теорема.
Если ф-я y=f(x)
определена и непрерывна на отрезке [a;
b],
диф-ма на интервале (a;
b),
то если f
'(x)
>= 0 на интервале (a;
b),
то ф-я неубывающая и если f
'(x)
> 0, то ф-я возрастающая. Док-во: Пусть
ф-я удовлетворяет неравенство a
< b
и x1
< x2
⇒
![]() тогда на отрезке
[a;
b]
она удовлетворяет условиям теоремы
Лагранджа ⇒
выполняется равенство: f
(x2)
– f
(x1)
= f
'(c)
* (x2
– x1)
⇒
f(x2)
>= f(x1)
– неубывающая; f(x2)
> f(x1)
– возрастающая. Теорема. Пусть ф-я y=f(x)
удовлетворяет всем условиям: 1) определена
и непрерывна на [a;
b];
2) дифференцируема на [a;
b]
=> для любых x
из (a;
b),
если f
'(x)<=0
ф-я не возрастающая. f
'(x)<0
– ф-я убывающая. Пример.
тогда на отрезке
[a;
b]
она удовлетворяет условиям теоремы
Лагранджа ⇒
выполняется равенство: f
(x2)
– f
(x1)
= f
'(c)
* (x2
– x1)
⇒
f(x2)
>= f(x1)
– неубывающая; f(x2)
> f(x1)
– возрастающая. Теорема. Пусть ф-я y=f(x)
удовлетворяет всем условиям: 1) определена
и непрерывна на [a;
b];
2) дифференцируема на [a;
b]
=> для любых x
из (a;
b),
если f
'(x)<=0
ф-я не возрастающая. f
'(x)<0
– ф-я убывающая. Пример.
20. Локальный экстремум. Необходимое условие экстремума. Пусть y=f(x) диф-ма на интервале (a; b). Точка x0 из (a; b) называется точкой локального минимума ф-и f(x), если существует такая окр-ть точки x0, то для всех x этого интервала выполняется неравенство. x0∈(a; b). f(x) ⩾ f(x0) (1). Точка x0 из интервала (a; b) называется точкой локального максимума f(x), если существует такая окр-ть точки x0, что для всех x выполняется неравенство f(x) ⩽ f(x0) (2). Если неравенство (1) строгое и неравенство (2) тоже строгое ⇒ точка x0 называется точкой строгого локального минимума и строгого локального максимума соответственно. Опр. Точки локального минимума и максимума называются экстремальными точками или точками экстремума ф-и.
Теорема (необходимое условие экстремума). Если y=f(x) определена и непрерывна в некоторой окр-ти точки x0, включая саму точку x0 и в этой точке имеется экстремум, то производная в ней равна 0 или не существует. Док-во: пусть точка x0 – точка экстремума ⇒ по теореме Ферма производная в этой точке равна 0. Замечание. Полезность этой теоремы состоит в том, что она позволяет отсеять лишние точки и оставить только те, в которых экстремум может быть. Теорема (1-ая достаточное условие экстремума).
21. Достаточные условия экстремума (по первой и второй производной). Теорема (1-ое достаточная условия экстремума). Пусть ф-я y=f(x) удовлетворяет следующим условиям: 1) Определена и непрерывна в точке x0 из отрезка [a; b] → x0∈ [a; b]; 1) Диф-ма в окр-ти точки x0; 3) Точка x0 – критическая точка ⇒ при переходе через точку x0 слева направо производная ф-и меняет свой знак с + на -, точка x0 – точка локального максимума. Если производная ф-и меняет свой знак с – на +, то точка x0 – точка локального минимума. Если производная не меняет свой знак, то в точке x0 экстремума нет. Теорема (2-ое достаточное условие экстремума). Пусть ф-я y=f(x) удовлетворяет следующим условиям: 1) Определена и непрерывна в точке x0 из отрезка [a; b]; 2) Точка x0∈ [a; b] – критическая точка; 3) Ф-я дважды непрерывно дифференцируема на интервале (a; b). (у неё есть вторая производная), тогда если в точке x0 f ''(x) < 0, то точка x0 – точка локального максимума. Если f ''(x) > 0, то точка x0 – точка локального минимума. Док-во: Пусть в точке x0 f ''(x)<0<(f '(x))'<0, то f '(x) существует на всём промежутке по признаку убывания возрастания ф-и, ф-я убывающая, а в точке x0 по условию теоремы f '(x) = 0 ⇒ в окрестности точки x0 f '(x) меняет знак с + на -, по 1-ому достаточному условию точки x0 – точка локального максимума. Пример.
22. Направление выпуклости графика функции. Условие выпуклости (по второй производной).
Опр.
Мн-во Е называется выпуклым, если для
любых 2-х точек М1 и М2, лежащих в этом
мн-ве провести соединяющий их отрезок,
то все точки этого отрезка будут лежать
внутри мн-ва Е, то это мн-во Е, называется
выпуклым.
![]() Опр. Пусть ф-я y=f(x)
определена и диф-ма на интервале (a;
b).
Будем называть график этой ф-и выпуклым
вверх если мн-во точек, лежащих под
графиком выпукло, тогда наш график
выпуклый вверх.
Опр. Пусть ф-я y=f(x)
определена и диф-ма на интервале (a;
b).
Будем называть график этой ф-и выпуклым
вверх если мн-во точек, лежащих под
графиком выпукло, тогда наш график
выпуклый вверх.
 Аналогично. Опр. График ф-и y=f(x)
называется выпуклой вниз на (a;
b),
если мн-во точек, лежащих над графиком
этой ф-и выпуклы.
Аналогично. Опр. График ф-и y=f(x)
называется выпуклой вниз на (a;
b),
если мн-во точек, лежащих над графиком
этой ф-и выпуклы.
 Теорема 1. Пусть ф-я y=f(x)
дважды непрерывна, диф-ма на (a;
b),
если f
''(x)
< 0, то ф-я выпукла вверх на этом интервале.
Теорема 2. Пусть ф-я y=f(x)
дважды непрерывна, диф-ма на интервале
(c;
d),
если f
''(x)>0,
то ф-я выпукла вниз на этом интервале.
Теорема 1. Пусть ф-я y=f(x)
дважды непрерывна, диф-ма на (a;
b),
если f
''(x)
< 0, то ф-я выпукла вверх на этом интервале.
Теорема 2. Пусть ф-я y=f(x)
дважды непрерывна, диф-ма на интервале
(c;
d),
если f
''(x)>0,
то ф-я выпукла вниз на этом интервале.
![]() Опр.
Пусть ф-я y=f(x)
дважды непрерывно диф-ма на интервале
(a;
b).
Точка М0(x0,
f(x0)),
где x0∈(a;
b) называется точкой перегиба графика
ф-и, если направление выпуклости графика
слева и справа различны.
Опр.
Пусть ф-я y=f(x)
дважды непрерывно диф-ма на интервале
(a;
b).
Точка М0(x0,
f(x0)),
где x0∈(a;
b) называется точкой перегиба графика
ф-и, если направление выпуклости графика
слева и справа различны.

23. Точки перегиба графика функции. Необходимое условие перегиба. Достаточные условия перегиба. Теорема (Необходимое условие перегиба). Если точку M0 (x0, f(x0)), при x0∈(a; b) яв-ся точкой перегиба графика ф-и y=f(x) и если эта точка дважды дифференцируема на этом интервале, то f ''(x0) = 0. Док-во: предположим, что f ''(x0) ≠ 0 ⇒ она должна быть f ''(x0) >/< 0. По условию в некоторой окр-ти существует f '(x), т.е. можно провести касательную. Если f '(x0)>0, то ф-я выпуклой вниз, точка x0 не является точкой перегиба, что противоречит условию теоремы. Теорема (1 достаточное условие перегиба). Пусть y=f(x) удовлетворяет следующим условиям: 1) Дважды непрерывно диф-ма на интервале (a; b); 2) Точка x0∈(a; b) и f ''(x0) =0, тогда если знаки второй производной слева и справа от точки x0 различны, то точка x0 является точкой перегиба, а если знаки второй производной слева и справа от точки x0 одинаковы, то точка x0 не является точкой перегиба. Замечание. Из опр. точки перегиба следует, что если в этой точке к графику ф-и провести касательную, то графики ф-и перейдёт от одной стороны в другую. Теорема (2 достаточное условие перегиба). Пусть ф-я y=f(x) трижды диф-ма на интервале (a; b) и в точке x0 вторая производная =0, тогда если f ''(x) ≠ 0, то точка М0(x0, f(x0)) будет точкой перегиба. Пример.
