(Карина) Формула Тейлора.
1.Функции
одной переменной.
Теорема A.
Если
в U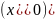
∃
,…,
,
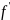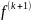то для x ∈ U
:
.
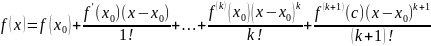(остаточный член в ф. Лагранжа)Где
c=tx+(1-t)
,t
∈ (0;1).
Об.:dx=x-
.
Перепишем
Т.A.:
Теорема B.
Если f-функция из
Т.A., то для x ∈ U(
):
f(x)=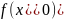
+
.
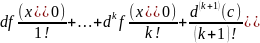Где
c=tx+(1-t)
,t
∈ (0;1).
2.Функции нескольких
переменных.
Теорема 1.
Если
f(x)=f(
,…,
)
(k+1) раз диф.-ма в U
.
Тогда для x ∈ U
:
f(x)=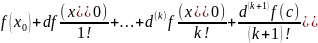
.
(остаточный член в формуле Лагранжа)Где
c=tx+(1-t)
,t
∈ (0;1).
Док.-во:
Пусть x ∈
U(
).
z*x+(1-z)
,где
z ∈ [0;1].
Рассмотрим φ(z)=f((zx)+(1-z)
)-функция
1 переменной, имеет
,…,
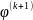в U(0)
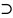[0;1].
(т.B.)
напишем раз.-е ϕ по формуле Тейлора в
точке z=1:
.
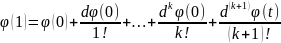Где t ∈ (0;1).
f(x)=
.
Ч.т.д.
Теорема 2.
Если f(x) k раз диф.-ма
в
∈ U(
):
f(x)=f(
)+
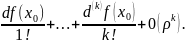(остаточный
член в форме Пеано)Где ρ=ρ(расст.)(x,
).
Без
док.-ва.
(Геля) Экстремумы (необходимое условие, достаточное условие, следствие для функций двух переменных).
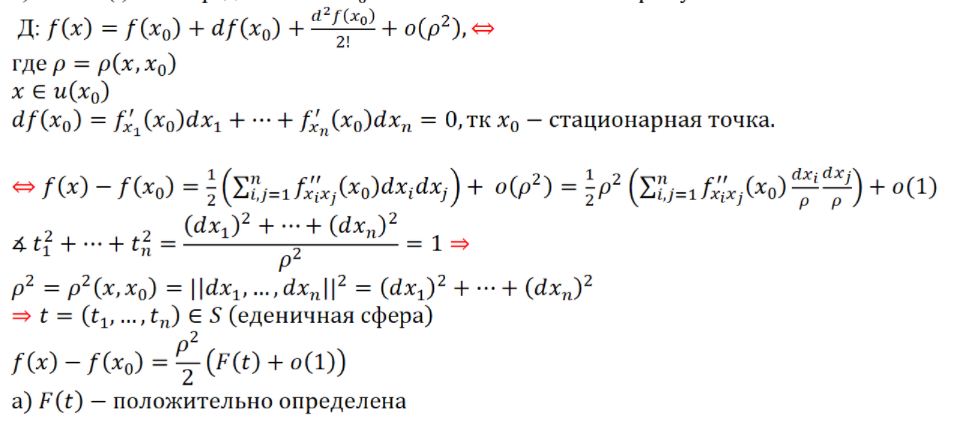
(Алина) Неявные функции, теорема об обратной функции.
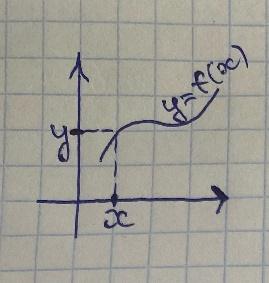
y=f(x)-явно
заданная функция.
y=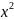
.
1.Функция
одной переменной.
F(x,y)=0.(1)
Опр. Если
∀ x из U(
)
уравнение (1) определяет функцию y=f(x),
т.е. ∀ x ∈ U(
)
∃! y, т.к. выполнилось (1), то функция y=f(x)
называется неявной функцией, заданной
в U(
).
Пример:
+
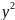-1=0.(2)
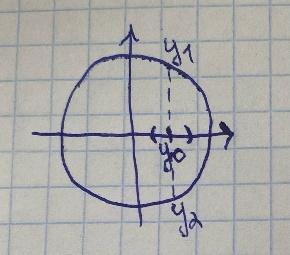x
∈ (-1;1).
(2) не задаёт неявную
функцию.
+
-1=0-определяет
неявную функцию при y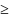
0.
Теорема
1(о неявной функции 1 переменной).
Пусть
=(
,
)
∈
,
F(x,y)=0.(1)
F такая, что:
1)F(
)=0.
2)F-непрерывна
в U(
).
3)F
имеет непрерывные частные производные
(
,
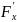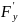) в U(
).
4)
(
)
0.
Тогда
∃ прямоугольник (
-δ;
+δ)*(
-
;
+
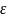)=P(
)
⊂ U(
)
такой, что в U(
)
уравнение (1) будет опр. неявную функцию
y=f(x) со знач. в U(
),
причем:
а)f(
)=
.
б)f(x)
непр. в U(
).
в)∃
f '(x)= -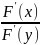
,
(x,f(x)) в U(
).
2.Неявные
функции нескольких
переменных.
F(
,…
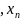,y)=0.(3)
=(
,…,
).
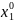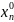Опр.
Если ∀ x ∈ U(
)
∃! Y, т.ч. (3), то уравнение (3) в U(
)
задает неявную функцию y=f(
,…,
).
Теорема
2(о неявной функции нескольких
переменных).
Пусть
=(
,…,
,
),
F
,…
,y)=0(3),
F т.ч.:
1)F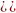
)=0.
2)F-непрерывна
в U(
).
3)F
имеет непрерывные частные производные
(
,
)
в U(
).
4)
(
)
0.
Тогда
∃ цилиндрическая окрестность U(
)*U(
),
т.ч. в U(
)
уравнение (3) определяет неявную функцию
y=f(
,…,
)
со значениями в U(
),
причем:
а) f(
)=
.
б)f
непр. в U(
).
в)∃
все частные производные
=
-
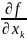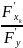непр. в U(
).
3.Матрицы
Якоби, Якобиан.
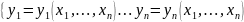диф.-мы в обл. D ⊂
.
Матрица
Якоби:
.
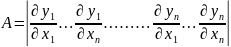Якобиан:
=
=
.
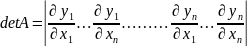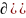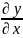4.Система
неявных функций.
(4).
Опр.
Если для любого x=
∈ U(
)
∃! y=(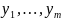
),
для которых выполняется (4), то в U(
)
(4) задает систему неявных функций.
(5).
Теорема
3(о системе неявных функций).
Пусть
=(
,…,
,…,
)
∈
,
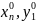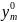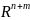есть система (4), т.ч.
:
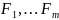1)
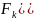)=0.
2)
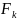-непрерывна
в U(
).
3)
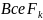имеют непрерывные частные производные
в U(
).
4)
0.
Тогда
∃ U(
),
U(
),
U(
)*U(
)
⊂ U(
),
т.ч. (4) в U(
)
задает систему неявных функций вида
(5). Причем:
а)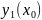
=
…
=
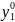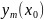б)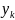
-непрерывна
в U(
).
в)
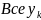имеют частные производные в U(
).