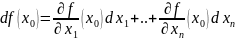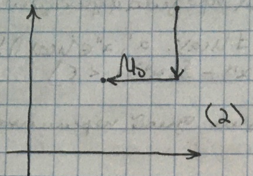
(Геля) Повторные пределы.
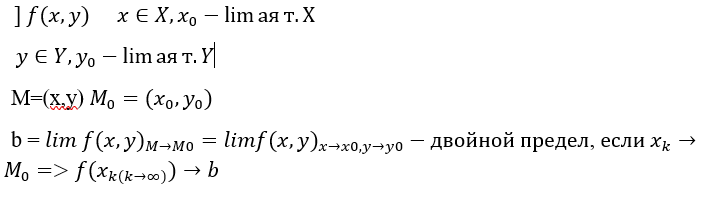
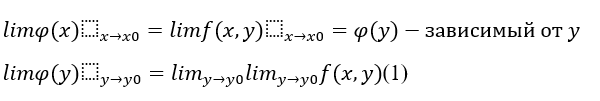
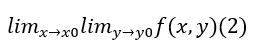
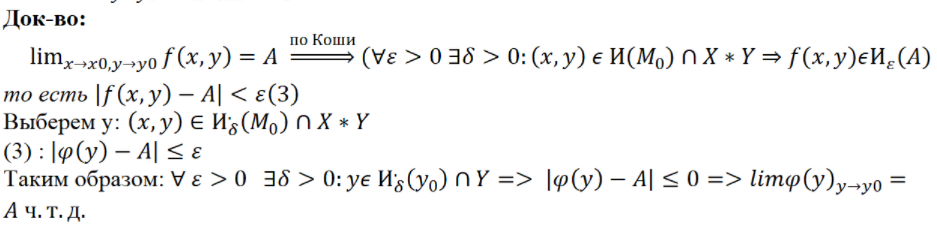
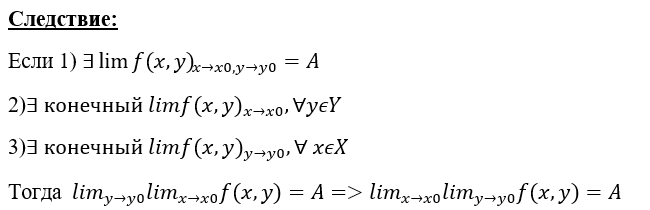
(Алина) Непрерывность функции в точке.
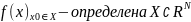
Опр.
F
непрерывна в точке
,
если
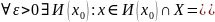
Свойства:
Совпадают со свойствами непрерывной функции одной переменной.
Если - изолированная точка множества Х, то f(x) непрерывна в
Если
-
предельная точка множества Х, то f(x)
непрерывна в
⬄
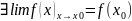
Сохранение
знака непрерывной функции в окрестности
точки непрерывности:
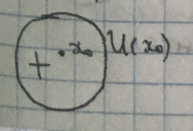
Арифметические операции
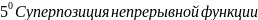
26.Линейно-связные множества и теорема Больцано-Коши о нуле.
Теорема А:(для функции одной переменной)
Если
f(x) непрерывна на [a;b], f(a)*f(b)<0, то
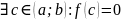
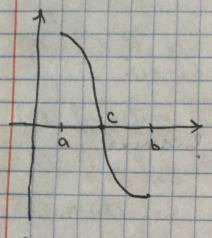
Опр.
f непрерывна на множестве Х, если f непрерывна в каждой точке этого множества.
Опр.
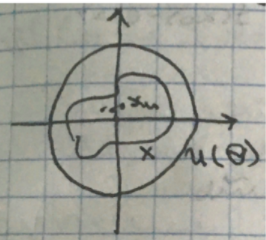
Множество
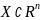называется линейно-связным, если две
любые точки этого множества можно
соединить кривой, лежащей в этом
множестве.
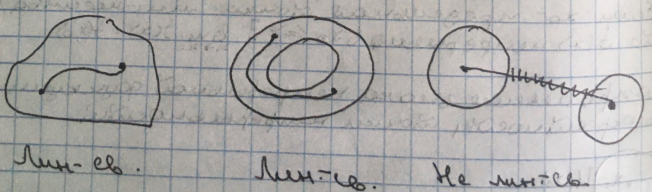
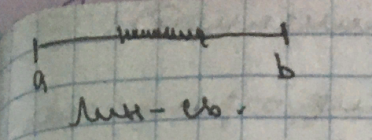
Теорема 1. (Больцано-Коши о нуле)
Если
f(x) непрерывна на линейно-связанном
множестве Х из
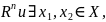в
которых f(x) принимает значения разных
знаков (f(
,
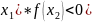то
(Карина) Линейно-связные множества и теорема Больцано-Коши о нуле.
Теорема А:(для функции одной переменной)
Если f(x) непрерывна на [a;b], f(a)*f(b)<0, то
Опр.
f непрерывна на множестве Х, если f непрерывна в каждой точке этого множества.
Опр.
Множество называется линейно-связным, если две любые точки этого множества можно соединить кривой, лежащей в этом множестве.
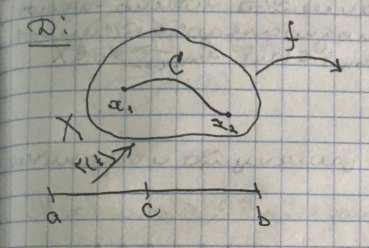
Теорема 1. (Больцано-Коши о нуле)
Если f(x) непрерывна на линейно-связанном множестве Х из в которых f(x) принимает значения разных знаков (f( , то
Доказательство:
X
– линейно связанное множество =>
,
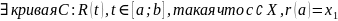r(b) =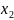
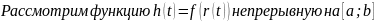
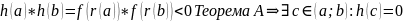
(Геля) Компактность и теорема Вейерштрасса.
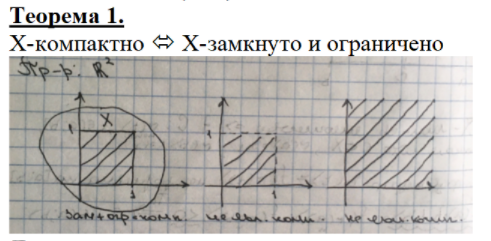
Теорема 2. (Вейерштрасса)
(Алина) Равномерная непрерывность.
f(x) ограничена на
Опр.
Функция
f равномерно непрерывна на Х, если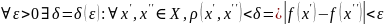
f(x) непрерывно равномерна на Х => (<≠) f(x) непрерывна на Х.
Теорема 1. (Кантора)
Непрерывная на компакте функция равномерно непрерывна.
(Карина) Частные производные, дифференцируемость, дифференциал.
f(x)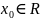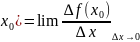
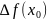f’(
=f(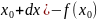
f(x)=f(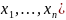
–
определена в И(
]
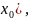
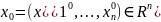
k: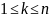
Зададим
приращения
к-ой координате вектора
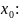Рассмотрим
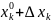
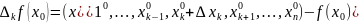
Приращение функции f по к=ой переменной (частное приращение функции f(x) )
Опр.1
Если
,
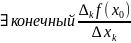то он называется частной производной
функции f(x) по переменной
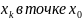
Обозначение.
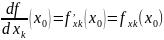
В
опр.1 меняем
,
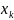а
остальные зафиксировали. => опр.1
опр.2
Опр.2
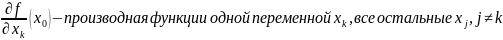считаем
константами.
Пример:
f(x,y,z)=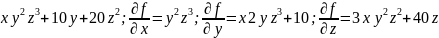
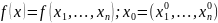
Зададим приращение каждой координате точки .
Рассмотрим
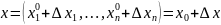
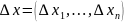
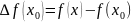– полное
приращение
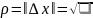
Опр.
Если
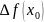может быть записана в виде
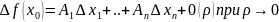
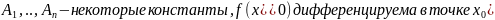
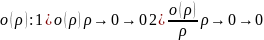
Опр.
Главная
(линейная) часть полного приращения
функции f называется дифференциалом
функции f в точке
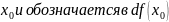
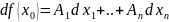
Теорема 1.
f(x)
– дифференцируема в точке
⬄
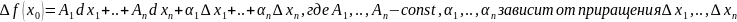
Д-во:
;
;
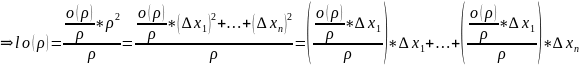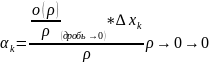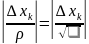
2)
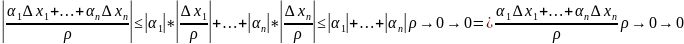ч.т.д.
Теорема 2.
Если f дифференцируема в точке , то f непрерывна в точке
Док-во
F
дифференцируема в точке
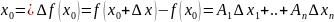
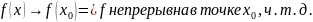
Для функции 1-ой переменной:
f(x)
дифференцируема в точке
⬄
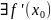
Теорема 3.
Если
f дифференцируема в точке
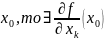и
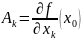
Обратное неверно !!!
Д-во:
f
– дифференцируема в точке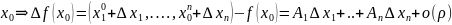
;
Зафиксируем к-ую координату:1
;
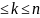Положим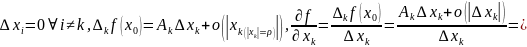
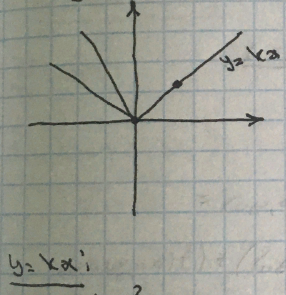
Обратное
неверно: Пример функции, имеющей все
частные производные, но не явл.
Дифференцируемой в точке
:
]
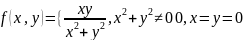
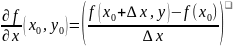
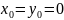
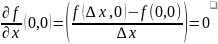
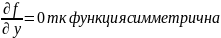
Расммотрим
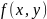
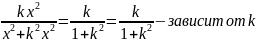
Значение
предела зависит от кривой =>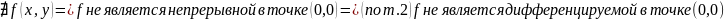
ч.т.д.
Следствие:
Если
f дифференцируема в точке
,
то
