Интерполяционный многочлен Лагранжа

Многочлен Лагранжа в основном используют для учебных целей, хотя его можно применять и на практике (в случае небольшого количества точек).

По заданному массиву точек (x_i, y_i), где i=0, 1, …, m интерполяционный многочлен Лагранжа определяется формулой:

, где

Рассмотрим конкретный пример. Распишем интерполяционный многочлен Лагранжа для трёх точек (i=0,…, 2):

Лабораторная работа № 8:

"Закраска произвольных областей"

Математические основы

Простой алгоритм заполнения с затравкой

В алгоритмах заполнения с затравкой предполагается, что известен хотя бы один пиксел из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пикселы, принадлежащие внутренней области. Области могут быть либо внутренне-, либо гранично-определенными. Если область относится к внутренне-определенным, то все пикселы, принадлежащие внутренней части, имеют один и тот же цвет или интенсивность, а все пикселы, внешние по отношению к области, имеют другой цвет. Это продемонстрировано на рис. 2.12. Если область относится к гранично-определенным, то все пикселы на границе области имеют выделенное значение или цвет, как это показано на рис. 2.13. Ни один из пикселов из внутренней части такой области не может иметь это выделенное значение. Тем не менее пикселы, внешние по отношению к границе, также могут иметь граничное значение. Алгоритмы, заполняющие внутренне-определенные области, называются внутренне-заполняющими, а алгоритмы для гранично-определенных областей - гранично-заполняющими. Далее будут обсуждаться гранично-заполняющие алгоритмы, однако соответствующие внутренне-заполняющие алгоритмы можно получить аналогичным образом.

Внутренне- или гранично-определенные области могут быть 4-или 8-связными. Если область 4-связная, то любого пиксела в области можно достичь с помощью комбинации движений только в 4 направлениях: налево, направо, вверх, вниз. Для 8-связной области пиксела можно достичь с помощью комбинации движений в двух горизонтальных, двух вертикальных и 4 диагональных направлениях (рис. 2.14).

Далее речь в основном пойдет об алгоритмах для 4-связных областей, однако их можно легко переделать для 8-связных областей, если заполнение проводить не в 4, а в 8 направлениях.

Используя стек, можно разработать простой алгоритм заполнения гранично-определенной области. Стек - это просто массив или другая структура данных, в которую можно последовательно пометить значения и из которой их можно последовательно извлекать. Когда новые значения добавляются или помещаются в стек, все остальные значения опускаются вниз на один уровень. Когда значения удаляются или извлекаются из стека, остальные значения всплывают или поднимаются вверх на один уровень. Такой стек называется стеком прямого действия. Простой алгоритм заполнения с затравкой можно представить в следующем виде:

Простой алгоритм заполнения с затравкой и стеком. Поместить затравочный пиксел в стек Пока стек не пуст   Извлечь пиксел из стека   Присвоить пикселу требуемое значение   Для каждого из соседних к текущему 4-связных пикселов проверить: является ли он граничным пикселом или   не присвоено ли уже пикселу требуемое значение. Проигнорировать пиксел в любом из этих двух случаев.   В противном случае поместить пиксел в стек.

Приведем более формальное изложение алгоритма, в котором предполагается существование затравочного пиксела и гранично-определенной области: Затравка(х, у) - выдает затравочный пиксел Push - процедура, которая помещает пиксел в стек Pop - процедура, которая извлекает пиксел из стека

Пиксел(х, у) = Затравка(х, у)
Push Пиксел(х, у) while (стек не пуст)	/ инициализируем стек
Pop Пиксел(х, у) if Пиксел(х, у) <> Нов_значение then Пиксел(х, у) = Нов_значение end if	/ извлекаем пиксел из стека
if (Пиксел(х + 1, у) <> Нов_значение and Пиксел(х + 1, у) <> Гран_значение) then Push Пиксел (х + 1, у) if (Пиксел(х, у + 1) <> Нов_значение and Пиксел(х, у + 1) <> Гран_значение) then Push Пиксел (х, у + 1) if (Пиксел(х - 1, у) <> Нов_значение and Пиксел(х - 1, у) <> Гран_значение) then Push Пиксел (х - 1, у) if (Пиксел(х, у — 1) <> Нов_значение and Пиксел(х, у - 1) <> Гран_значение) then Push Пиксел (х, у - 1) end if end while

Пример 2.3. Алгоритм заполнения многоугольника с затравкой. В качестве примера применения алгоритма рассмотрим гранично-определенную область, содержащую дыру. Она изображена на рис. 2.15.

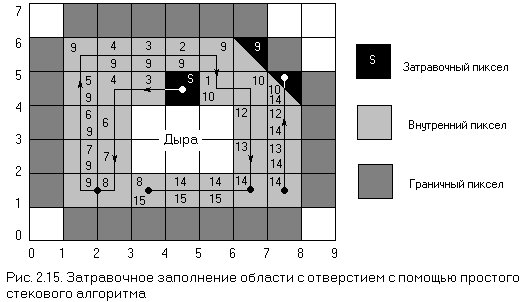
Вершины многоугольника заданы пикселами (1,0), (7,0), (8,1), (8,4), (6,6), (1,6), (0,5) и (0,1). Внутренняя дыра определяется пикселами (3,2), (5,2), (5,3), (3,3). Затравочный пиксел — (4,4). Порядок заполнения указан на рисунке линией со стрелками. Числа в квадратике пиксела показывают позицию в стеке, занимаемую пикселом. Когда обработка доходит до пиксела (3,1), все окружающие его 4-связные пикселы либо уже заполнены, либо являются граничными. Поэтому ни один из пикселов не помещается в стек. Глубина стека в этот момент равна 15. В стеке находятся пикселы (7,1), (7,2), (7,3), (6,5), (7,4), (6,5), (3,1), (1,2), (1,3), (1,4), (2,5), (3,5), (4,5), (5,4).

После удаления из стека пиксела (7,1) заполняется колонка (7,1), (7,2), (7,3), (7,4), при этом ни один новый пиксел в стек не добавляется. Для пиксела (7,4) снова все 4-связные окружающие пикселы либо уже заполнены, либо являются граничными. Обращаясь к стеку, алгоритм извлекает пиксел (6,5), его заполнение завершает заполнение всего многоугольника. Дальнейшая o6работка происходит без какого-либо заполнения, и когда стек становится пустым, алгоритм завершает работу.

Построчный алгоритм заполнения с затравкой

Как видно из предыдущего примера, стек может стать довольно большим. Еще один недостаток предыдущего алгоритма - стек зачастую содержит дублирующую или ненужную информацию. В построчном алгоритме заполнения с затравкой размер стека минимизируется за счет хранения только одного затравочного пиксела для любого непрерывного интервала на сканирующей строке. Непрерывный интервал - это группа примыкающих друг к другу пикселов (ограниченная уже заполненными или граничными пикселами). Мы для разработки алгоритма используем эвристический подход, однако также возможен и теоретический подход, основанный на теории графов.

Данный алгоритм применим к гранично-определенным областям. Гранично-определенная 4-связная область может быть как выпуклой, так и не выпуклой, а также может содержать дыры. В области, внешней и примыкающей к нашей гранично-определенной области, не должно быть пикселов с цветом, которым область или многоугольник заполняется. Схематично работу алгоритма можно разбить на четыре этапа.

1. Затравочный пиксел на интервале извлекается из стека, содержащего затравочные пикселы.

2. Интервал с затравочным пикселом заполняется влево и вправо от затравки вдоль сканирующей строки до тех пор, пока не будет найдена граница.

3. В переменных Х_лев и Х_прав запоминаются крайний левый и крайний правый пикселы интервала.

4. В диапазоне Х_лев <= x <= X_прав проверяются строки, расположенные непосредственно над и под текущей строкой. Определяется, есть ли на них еще не заполненные пикселы. Если такие пикселы есть (т. е. не все пикселы граничные, или уже заполненные), то в указанном диапазоне крайний правый пиксел в каждом интервале отмечается как затравочный и помещается в стек.

5. При инициализации алгоритма в стек помещается единственный затравочный пиксел, работа завершается при опустошении стека.

Как показано в примере ниже, алгоритм справляется с дырами и зубцами на границе. Ниже приводится более подробное описание алгоритма на псевдокоде:

Затравка (х,у) - выдает затравочный пиксел Pop - процедура, которая извлекает пиксел из стека Push - процедура, которая помещает пиксел в стек

Push Затравка (х, у) while (стек не пуст)	/ инициализируем стек
Pop Пиксел (х, у) Пиксел (х, у) = Нов_значение	/ извлекаем пиксел из стека и присваиваем ему новое значение
Врем_х = х	/ сохраняем x-координату затравочного пиксела
х = х + 1 while Пиксел (х, у) <> Гран_значение Пиксел (х, у) = Нов_значение х = х + 1 end while	/ заполняем интервал справа от затравки
Хправ = х — 1	/ сохраняем крайний справа пиксел
х = Врем_х	/ восстанавливаем х-координату затравки
х = х — 1 while Пиксел (х, у) <> Гран_значение Пиксел (х, у) = Нов_значение х = х — 1 end while	/ заполняем интервал слева от затравки
Хлев = х + 1	/ сохраняем крайний слева пиксел
х = Врем_х	/ восстанавливаем х-координату затравки
х = Хлев у = у + 1 while х <= Хправ	/ проверим, что строка выше не является ни границей мно- гоугольника, ни ухе полностью заполненной; если это не так, то найти затравку, начиная с левого края подынтер- вала сканирующей строкивосстанавливаем х-координату затравки
Флаг = 0 while (Пиксел (х, у) <> Гран_значение and Пиксел (х, у) <> Нов_значение and х < Хправ if Флаг = 0 then Флаг = 1 x = x + 1 end while	/ ищем затравку на строке выше
if Флаг = 1 then if (x = Хправ and Пиксел (х, у) <> Гран_значение and Пиксел (х, у) <> Нов_значение) then Push Пиксел (х, у) elsePush Пиксел (х — 1, у) end if Флаг = 0 end If	/ помещаем в стек крайний справа пиксел
Хвход = х while ((Пиксел (х, у) = Гран_значение оr Пиксел (х, у) = Нов_значение) and х < Хправ) х = х + 1 end while	/ продолжим проверку, если интервал был прерван
if х = Хвход then х = х + 1 end while	/ удостоверимся, что координата пиксела увеличена
эта часть алгоритма совершенно аналогична проверке для строки выше, за исключением того, что вместо y = y + 1 надо подставить y = y — 1 end while finish	/ проверим, что строка ниже не является ни границей многоугольника, ни уже полностью заполненной

Пример 2.4. Построчный алгоритм заполнения с затравкой. Рассмотрим работу алгоритма для гранично-определенной области на рис. 2.16. При инициализации в стек помешается затравочный пиксел, помеченный как Затравка (5,7) на рис. 2.16,а. Первоначально в качестве затравки интервала из стека извлекается этот пиксел. Интервал заполняется справа и слева от затравки. Найденные при этом концы интервала Х_прав = 9 и X_лев = 1. Затем проверяется строка, расположенная выше текущей и оказывается, что она не граничная и не заполненная. Крайним правым пикселом в диапазоне 1 <= x <= 9 оказывается пиксел (8,8), помеченный цифрой 1 на рис. 2.16,а. Этот пиксел помещается в стек. Затем аналогичным образом обрабатывается строка ниже текущей. В диапазоне Х_лев <= x <= X_прав есть два подинтервала на этой стороне. Для левого интервала в качестве затравки выступает пиксел (3,6), помеченный цифрой 2 на рис. 2.16,а, он тоже помещается в стек. Затравка для правого подинтервала - пиксел (9,6), он помещается в стек. Заметим, что пиксел (9,6) - не самый крайний правый пиксел на интервале, однако это самый крайний правый пиксел в диапазоне Х_лев <= x <= X_прав, т.е. в диапазоне 1 <= x <= 9. На этом завершается первый проход алгоритма.

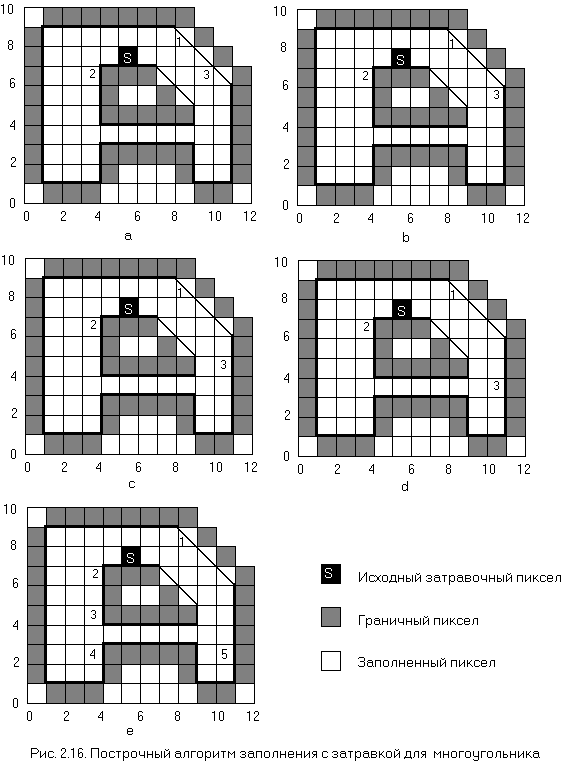
Далее из стека извлекается верхний пиксел. Здесь заполняются интервалы, расположенные в правой части многоугольника на последовательных сканирующих строках (рис. 2.16, b, c, d). Для строки 3 затравкой служит пиксел (10,3) (рис. 2.16, d). В результате заполнения интервала справа и слева от затравки получаем новые пределы диапазона Х_прав = 10 и X_лев = 1. Обрабатывая строку выше, получаем для основного подынтервала затравочный пиксел (3,4), коорый помещается в стек. Правый подинтервал к этому времени уже заполнен. Обработка строки ниже дает затравку (3,2) для левого и (10,2) для правого подынтервалов. Эти пикселы также помещаются в стек. Именно сейчас достигается максимальная глубина стека для обрабатываемого многоугольника.

Теперь остается только один интересный момент. После заполнения 4-связных полигональных подобластей с затравочными пикселами 5, 4 и 3 на рис. 2.16,е из стека извлекается пиксел, помеченный цифрой 2. Здесь мы обнаруживаем, что все пикселы на этой строке уже и на соседних строках (выше и ниже) уже заполнены. Таким образом, ни один пиксел в стек не помещается. Из стека извлекается пиксел 1 и строка обрабатывается, при этом вновь добавочных пикселов не появляется. Теперь стек пуст, многоугольник заполнен и работа алгоритма завершена.

По сравнению с алгоритмом из разд. 2.7 максимальная глубина стека в этом примере равна пяти.