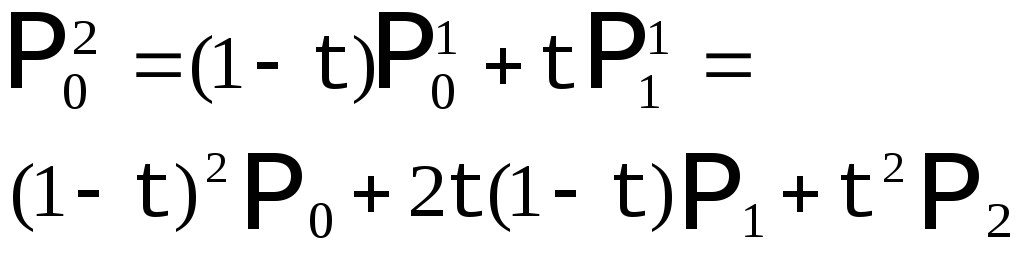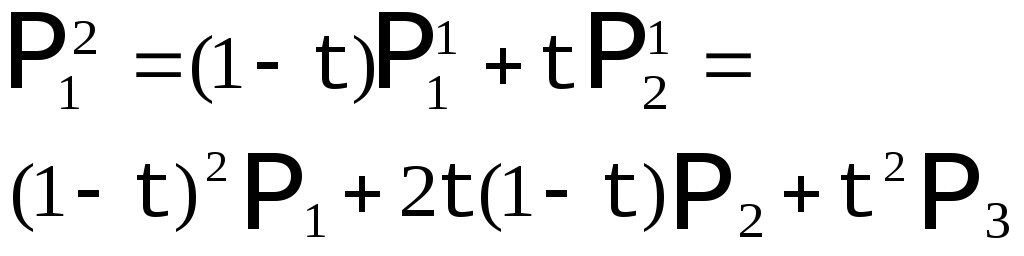1) Кривые Безье

В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно).

Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 8). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.

Рис. 8. Кривая Безье с 3 опорными точками.

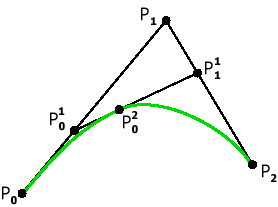
Обозначим опорные точки как ,, начало кривой положим в точке (t=0), а конец в точке (t=1), для каждого найдем точку , таким образом, получим кривую второго порядка.

Теперь построим аналогичным методом кривую Безье с 4 опорными точками.

Рис. 9. Кривая Безье с 4 опорными точками.

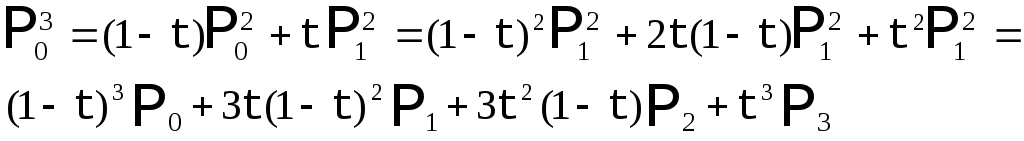
Можно продолжать подобные построения и для большего числа узлов, получая аналогичные выкладки. Запишем общее аналитическое представление для кривой Безье с N+1 опорной точкой:

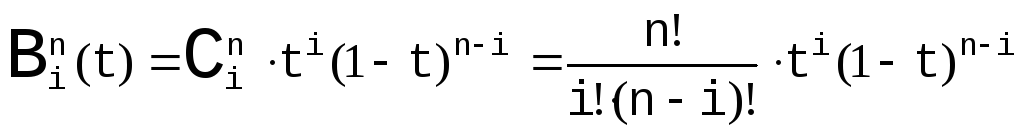, где , где- биномиальные коэффициенты,

называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна).

Лабораторные основы

Цель работы: изучить интерполяционный многочлен Лагранжа и научиться вычислять параметры для аппроксимирующих функций, чтобы строить графики зависимостей для произвольных наборов точек.

Основные понятия, используемые в лабораторной работе: Аппроксимация и интерполяция: различие и сходство. Метод наименьших квадратов. Многочлен Лагранжа.

Под аппроксимацией обычно понимают операцию сглаживания, которая призвана уменьшить осцилляции, обусловленные неверными значениями некоторых координат. Задача аппроксимации возникает тогда, когда по заданному массиву точек [x_i, y_i], где i=0, 1, …, m, требуется построить функцию, проходящую не через заданные точки, а вблизи них, и изменяющуюся достаточно плавно.

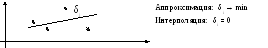
Метод наименьших квадратов

Предположим, у нас имеется набор экспериментальных точек зависимости Y от X . Возникает вопрос, как по этим экспериментальным точкам наилучшим образом воспроизвести зависимость Y от X? Для решения подобных задач обычно применяется расчетный метод, известный под названием "Метод наименьших квадратов". Этот метод дает возможность при заданном типе зависимости Y=f(X) так выбрать ее числовые параметры, чтобы график зависимости Y=f(X) наилучшим образом отображал экспериментальные данные. Тип зависимости Y=f(X), как правило, выбирается исходя из внешнего вида полученного набора точек. Он может быть линейным, квадратичным, экспоненциальным и т.д. . В методе наименьших квадратов под условием «наилучшим образом» понимают следующее требование: "Сумма квадратов отклонений экспериментальных точек от сглаживающей кривой должна быть минимальной".

Рассмотрим линейную зависимость. Пусть имеется набор из n экспериментальных точек с координатами (х₁, y₁), (х₂, у₂), ..., (х_n, у_n). Предполагается, что точки отображают линейную зависимость. Требуется подобрать по методу наименьших квадратов коэффициенты а и b линейной функции у = ах + b.

Решение. Запишем у как функцию не только аргумента х, но и параметров а и b (так как величины а и b неизвестны ):

у = f (х; a, b) = ax + b (1)

Требуется выбрать а и b так, чтобы выполнялось условие: "Сумма квадратов отклонений экспериментальных точек от построенной линейной зависимости должна быть минимальной", то есть для набора n экспериментальных точек должно быть выполнено условие :

(2)

или

где у_i - значение у-координаты i-ой точки из набора экспериментальных точек, х_i - значение x-координаты i-ой точки из набора экспериментальных точек, (ах_i + b) - значение функции у = ах + b в i-ой точке.

Найдём значения а и b, при которых левая часть выражения (2) обращается в минимум. Для этого продифференцируем её по а и b; приравняем производные нулю:

;(3)

где - значение частной производной функции у(х) = ах +b по параметру а в точке c координатами (х_i, у_i) , а - значение частной производной функции по параметруb.

Система уравнений (3) содержит столько уравнений, сколько неизвестных коэффициентов в искомой зависимости. В нашем случае их два – а и b. Продифференцируем (1) по а и b, получим:

;

(4)

;

Подставим выражения (4) в (3) и получим два уравнения для определения а и b:

(5)

Раскроем скобки, просуммируем и получим:

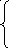(6)

, где n – число точек

Получили систему из двух уравнений с двумя неизвестными, которая легко решается.

Рассмотрим теперь конкретный пример. Пусть имеется набор из 3 экспериментальных точек с координатами (1,1), (2,2) и (3,0). Предполагается, что точки отображают линейную зависимость. Требуется найти коэффициенты а и b для линейной функции у = ах + b.

Решение.

Xi	Уi
1	1
2	2
3	0

Воспользуемся системой уравнений (6) и подставим в неё координаты экспериментальных точек. Получаем следующую систему уравнений:

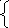
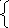
Решаем и получаем a = -0.5, b = 2. Таким образом, вид линейной функции: у = - 0.5 х + 2 .

Под интерполяцией понимают построение гладкой функции, проходящей через все заданные точки. Для этого применяют интерполяционные кубические сплайны, NURBS-сплайны, B-сплайны и т.п.
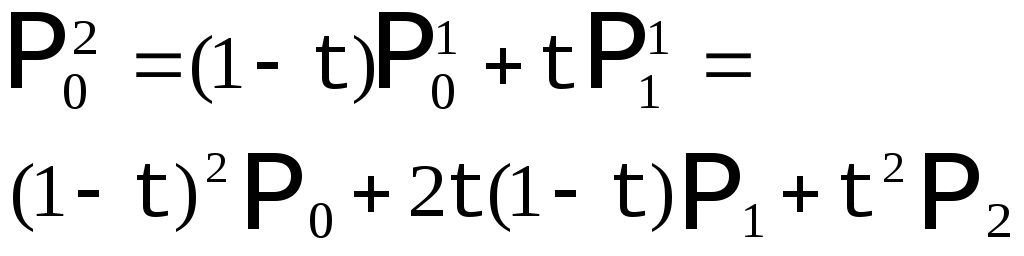