Лабораторная работа № 6:

"Геометрические преобразования.

Сдвиг, масштабирование, поворот, симметрия"

Математические основы

Двумерные преобразования

Преобразование точек

Точка представляется на плоскости двумя своими координатами, которые определяются как элементы матрицы размером 1х2 [х у]. В трехмерном пространстве используется матрица размером 1х3 [x у z]. Иначе говоря, точка может задаваться в виде вектор-столбца

	x  y

в двумерном пространстве или в виде

	x  y z

в трехмерном. Строку [х у] или столбец часто называют координатным вектором. Для формирования такого вектора используется матрица-строка, т. е. множество точек, каждая из которых определяет координатный вектор в некоторой системе измерения. Данное множество хранится в виде матрицы или массива чисел. Положением точек можно управлять путем манипулирования соответствующей матрицей. Линии, соединяющие точки, формируют отрезки, кривые и картинки.

В качестве элементов матрицы могут фигурировать различные величины: числа, сетки или коэффициенты системы уравнений. Правила в матричной алгебре определяют допустимые операции над элементами. Многие физические задачи удобно выражаются в матричном представлении. Для моделей физических систем задача обычно ставится следующим образом: даны матрицы [А] и [В], найти результирующую матрицу [Т], такую, что [А][Т] = [В]. В этом случае решением является матрица [Т] = [А]^-1[В], где [А]^-1 - матрица, обратная к квадратной матрице [А].

В то же время матрицу [Т] можно интерпретировать как геометрический оператор. В этом случае для выполнения геометрического преобразования точек, представленных векторами положений в матрице [А], используется умножение матриц. Предположим, что матрицы [А] и [T] известны. Требуется определить элементы матрицы [В]. Представление [T] как геометрического оператора является основой математических преобразований, используемых в машинной графике.

Рассмотрим результаты умножения матрицы [х у], содержащей координаты точки Р, на матрицу общего преобразования размером 2х2:

[X][T] = [x  y]		a   b  c   d		[(ax + cy) (bx + dy)]

Данная запись означает, что исходные координаты точки х и у преобразуются в х* и y*, где где х* = ах + су, у* = bх + dy. Представляют интерес значения х*, у* - координаты результирующей, преобразованной точки Р. Рассмотрим некоторые специальные случаи.

При а = d = 1 и с = b = 0 преобразование сведется к единичной матрице

[X][T] = [x  y]		1   0  0   1		[x  y] = [x*  y*]

и координаты точки Р останутся неизменными. Как и следовало ожидать, в линейной алгебре умножение на единичную матрицу эквивалентно умножению на 1 в обычной алгебре.

В случае d = 1, b = c = 0

[X][T] = [x  y]		а   0  0   1		[аx  y] = [x*  y*]

где х* = ах - результат масштабирования координаты х. Эффект показан на рисунке 1.1,а.

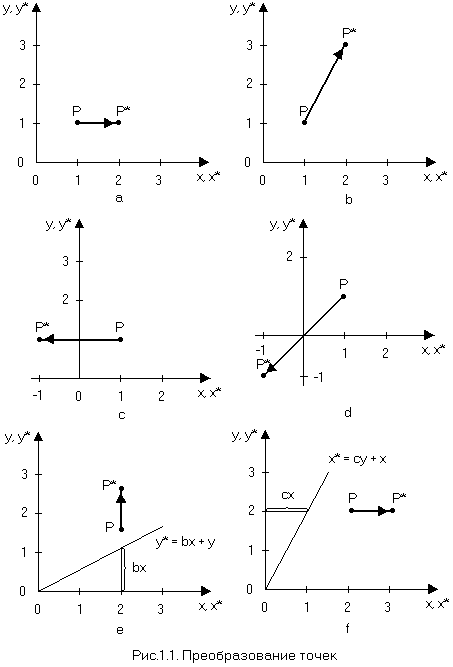
Рассмотрим теперь еще случай b = с = 0, т.е.

[X][T] = [x  y]		а   0  0   d		[аx  yd] = [x*  y*]

Данное преобразование вызывает изменение обеих координат х и у вектора Р (рис. 1.1,b). Если а <> d, то координаты масштабируются различным образом. При a = d > 1 происходит растяжение вектора Р или масштабирование координат. Если 0 < а = d < 1, то имеет место сжатие.

Если значение а или d отрицательное, то вектор отражается относительно координатных осей или относительно плоскости. Чтобы убедиться в этом, возьмем b = c = 0, d = 1 и а = 1, тогда

[X][T] = [x  y]		-1   0  0   1		[-x  y] = [x*  y*]

и в результате получаем симметричное отражение относительно оси y (рис. 1.1,c). Если b = c = 0, а = 1, d = -1, то выполняется симметричное отражение относительно оси х. Если b = с = 0, а = d < 0, то происходит отражение относительно начала координат, это показано на рисунке 1.1,d, где a = -1, d =1. Заметим, что обе операции отражения и масштабирование зависят только от диагональных членов матрицы преобразования.

Рассмотрим теперь случай с недиагональными членами. Возьмем сначала значения a = d = 1, c = 0, тогда

[X][T] = [x  y]		1   b  0   1		[x  (bx + y)] = [x*  y*]

Заметим, что координата х точки Р осталась неизменной, тогда как координата y линейно зависит от исходных координат. Данное преобразование называется сдвигом (рис. 1.1,e). Аналогично, в случае, когда а = d = 1, b = 0, преобразование приведет к сдвигу пропорционально координате y (рис. 1.1,f). Таким образом, видно, что недиагональные члены матрицы преобразования создают эффект сдвига координат вектора точки Р.

Прежде чем закончить с преобразованием точек, разберем действие общего преобразования, когда начальный вектор лежит в точке начала координат, т.е.

[X][T] = [x  y]		a   b  c   d		[(ax + cy) (bx + dy)]

или в случае начала координат,

[X][T] = [0  0]		a   b  c   d		[0  0] = [x*  y*]

Видно, что начало координат инвариантно относительно преобразования общего вида. Это ограничение устраняется при использовании однородных координат.

Преобразование параллельных линий

Прямую линию можно определить с помощью двух векторов, задающих координаты ее конечных точек. Расположение и направление линии, соединяющей две эти точки, может изменяться в зависимости от положения векторов.

Результатом преобразования двух параллельных линий с помощью (2х2)-матрицы снова будут две параллельные линии. Это можно увидеть, рассмотрев линию между точками [А] = [x₁ y₁], [В] = [х₂ y₂] и параллельную ей линию, проходящую между точками E и F. Покажем, что для этих линий любое преобразование сохраняет параллельность. Так как АВ, EF и A*B* и E*F* параллельны, то угол наклона линий АВ и EF определяется следующим образом:

m =	y2 - y1 x2 - x1

Преобразуем конечные точки АВ, воспользовавшись матрицей общего преобразования размером (2х2):

A  B

[T] =

x1   y1  x2   y2

a   b  c   d

=

ax1 + cy1   bx1 + dy1   ax2 + cy2   bx2 + dy2

=

x1*   y1*   x2*   y2*

=

A*  B*

Наклон прямой А*В* определяется следующим образом:

m* =

(bx2 + dy2) - (bx1 + dy1) (ax2 + cy2) - (ax1 + cy1)

=

b(x2 - x1) + d(y2 - y1) a(x2 - x1) + c(y2 - y1)

или

m* =	b + d	(y2 - y1) (x2 - x1)	=	b + dm a + cm
	a + c	(y2 - y1) (x2 - x1)

Так как наклон m* не зависит от х₁, х₂, y₁, y₂, а m, а, b, с и d одинаковы для EF и AB, то m* одинаково для E*F* и А*В*. Таким образом, параллельные линии сохраняют параллельность и после преобразования. Это означает, что при преобразовании (2х2) параллелограмм преобразуется в другой параллелограмм. Эти тривиальные выводы демонстрируют большие возможности использования матрицы преобразования для создания графических эффектов.

Преобразование пересекающихся прямых

Результатом преобразования с помощью (2х2)-матрицы пары пересекающихся прямых линий также будет пара пересекающихся линий. Проиллюстрируем это на примере двух прямых, заданных уравнениями:

y = m₁x + b₁ y = m₂x + b₂

В матричном представлении эти уравнения будут иметь вид:

[X][T] = [x   y]		-m1  -m2   1       1		= [b1   b2]

или

[X][M] = [B]

Если существует решение этой системы уравнений, то линии пересекаются, в противном случае они параллельны. Решение можно найти путем инверсии матрицы. В частности,

[X_i] = [x_i   y_i] = [B][M] ^-1

Матрица, обратная [М], имеет следующий вид:

				1 m2 - m1 -1m2 - m1		m2 m2 - m1 -m1 m2 - m1

так как [M][M] ^-1 = [E], где [E] - единичная матрица. Поэтому координаты точки пересечения двух линий можно найти следующим образом:

[Xi] = [xi  yi] = [b1  b2]				1 m2 - m1 -1m2 - m1		m2 m2 - m1 -m1 m2 - m1

[Xi] = [xi  yi] =				b1 – b2 m2 - m1		b1m2 - b2m1 m2 - m1

Если обе линии преобразовать с помощью (2х2)-матрицы общего преобразования вида:

[T] =		a   b  c   d

то их уравнения будут иметь вид

y* = m₁*x* + b₁* y* = m₂*x* + b₂*

Соответственно можно показать, что

mi* =

b + dmi a + cmi

и

bi* = bi(d - cmi*) = bi

ad - bc a + cmi

где i = 1, 2.

Точка пересечения линий после преобразования отыскивается таким же образом, что и в случае исходных линий:

[Xi*] = [xi*   yi*] =				b1* - b2* m2* - m1*		b1*m2* - b2*m1* m2* - m1*

Воспользовавшись тремя предыдущими выражениями, получим:

[Xi*] = [xi*   yi*] =				a(b1 - b2) + c(b1m2 – b2m1) m2 - m1		b(b1 - b2) + d(b1m2 - b2m1) m2 - m1

Возвращаясь теперь к точке пересечения [x_i y_i] исходных линий и применяя уже полученную матрицу преобразования, имеем

[xi*   yi*] = [xi   yi][T] =

b1 – b2 m2 - m1

b1m2 - b2m1 m2 - m1

a   b  c   d

=

=				a(b1 - b2) + c(b1m2 – b2m1) m2 - m1		b(b1 - b2) + d(b1m2 - b2m1) m2 - m1

Сравнение уравнений точек пересечения исходных линий и преобразованных показывает, что они одинаковы. Итак, точка пересечения преобразуется точно в другую точку пересечения.

Поворот

Рассмотрим треугольник ABC (рис.1.2) и с помощью следующего преобразования повернем его на 90° против часовой стрелки относительно начала координат

[T] =		0   1 -1   0

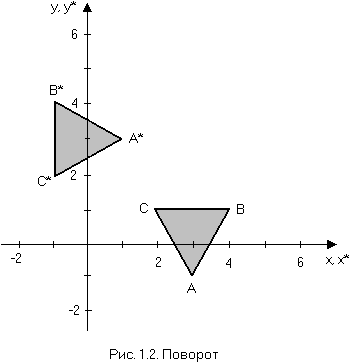
Если использовать матрицу (3 х 2), состоящую из координат x и y вершин треугольника, то можно записать

	3  -1 4   1 2   1			0   1 -1   0	=		3  -1 4   1 2   1

что является координатами результирующего треугольника A*B*C*. Поворот нв 180° относительно начала координат достигается путем следующего преобразования

[T] =		-1   0   0  -1

а на 270° относительно начала координат - преобразованием

[T] =		0  -1  1   0

Разумеется, что матрица тождественного преобразования

[T] =		1   0  0   1

соответствует повороту вокруг начала координат на 0° или на 360°.

Как осуществить поворот вокруг точки начала координат на произвольный угол θ? Для ответа на этот вопрос рассмотрим вектор положения от начала координат до точки Р (рис. 1.3). Обозначим r - длину вектора, а φ - угол между вектором и осью х. Вектор положения поворачивается вокруг начала координат на угол θ и попадает в точку Р*. Записав векторы положений для Р и Р*, получаем:

Р = [х   у] = [r cosφ   r sinφ]

и

Р* = [x*   у*] = [r соs(θ + φ)   r sin(θ + φ].

Используя формулу для cos суммы углов, перепишем выражение для Р* следующим образом

Р* = [x*   у*] = [r(cosφcosθ - sinφsinθ)   r(соsφsinθ + sinφcosθ)].

Используя определения х и у, можно переписать Р* как

Р* = [x*   у*] = [x cosθ - y sinθ   x sinθ + y cosθ].

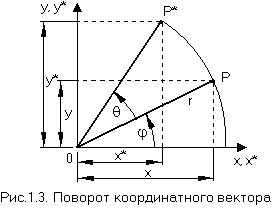
Таким образом, преобразованная точка имеет координаты

x* = x cosθ - y sinθ y* = x sinθ + y cosθ.

Или в матричном виде

[X*] = [X][T] = [x*   y*] = [x   y]		cosθ   sinθ  -sinθ   cosθ

Итак, преобразование поворота вокруг точки начала координат на произвольный угол θ задается матрицей

[T] =		cosθ   sinθ  -sinθ   cosθ

Отражение

В то время как полный поворот на плоскости xy обычно осуществляется в двумерном пространстве относительно нормали к плоскости, отражение представляет собой тот же поворот на угол 180° в трехмерном пространстве и обратно на плоскость относительно оси, лежащей в плоскости xy. На рис. 1.4 приведены примеры двух отражений на плоскости треугольника DEF. Отражение относительно прямой y = 0 (ось x) получено с использованием матрицы

[T] =		1   0  0  -1

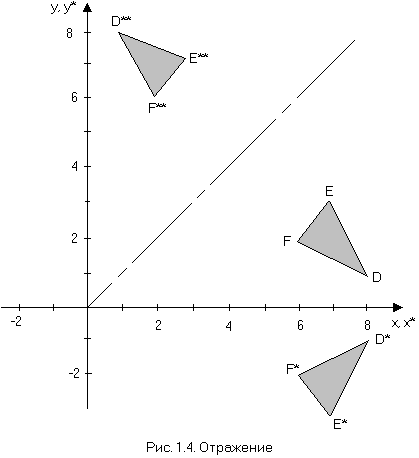
В этом случае новые вершины треугольника D*E*F* будут определяться преобразованием

	8   1 7   3 6   2			1   0  0  -1	=		8  -1 7  -3 6  -2

Подобным образом отражение относительно оси y при x = 0 будет иметь вид

[T] =		-1   0   0   1

Отражение относительно прямой y = x осуществляется с помощью матрицы

[T] =		0   1 1   0

Выполнив преобразования, получим координаты вершин треугольника D**E**F**

	8   1 7   3 6   2			0   1 1   0	=		1   8 3   7 2   6

Аналогичным образом отражение относительно оси x будет иметь вид

[T] =		0  -1 -1   0

Масштабирование

Величина масштабирования определяется значением элементов исходной диагональной матрицы. Если матрица

[T] =		2   0 0   2

используется в качестве оператора воздействия на вершины треугольника, то имеет место «двукратное» расширение или равномерное масштабирование относительно точки начала координат. Если значения элементов не равны, то треугольник искажается, что проиллюстрировано на рис.1.5. Треугольник ABC, преобразованный с помощью матрицы

[T] =		2   0 0   2

переходит в пропорционально увеличенный треугольник A*B*C*. Тот же треугольник, но преобразованный с помощью матрицы

[T] =		1/2   0   0    3

переходит в треугольник DEF, имеющий искажение, вызванное разными коэффициентами масштабирования.

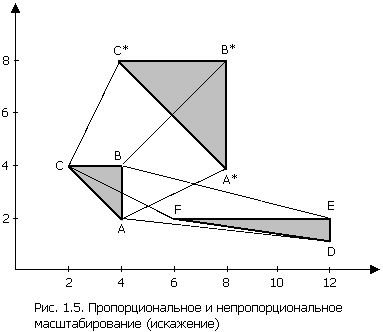
В общем случае при матрице

[T] =		a   b c   d

в которой а = d, b = с = 0, выполняется пропорциональное масштабирование; если a <> d, b = с = 0, то масштабирование будет проведено непропорционально. В первом случае для а = d > 1 происходит расширение, т.е. - увеличение изображения. Если а = d < 1, то происходит равномерное сжатие, т.е. фигура уменьшается. Непропорциональное расширение и сжатие возникают в зависимости от значений a и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.

Перемещения и однородные координаты

В предыдущих разделах был рассмотрен ряд преобразований, совершаемых с помощью (2х2)-матрицы общего преобразования. Среди них поворот, отражение, масштабирование, сдвиг и другие. Ранее отмечалось, что исходная система координат инвариантна по отношению ко всем перечисленным преобразованиям. Однако возникает необходимость изменять положение начала координат, т. е. преобразовывать каждую точку на плоскости. Этого можно достичь путем перемещения точки начала координат или любой другой точки на плоскости

x* = ax + cy + m, y* = bх + dy + n.

К сожалению, нельзя ввести константы перемещения m и n в (2х2)-матрицу преобразования, так как это не пространство!

Данное затруднение можно преодолеть, используя однородные координаты. Однородные координаты неоднородного координатного вектора [x y] представляют собой тройку [x' y' h], где x = x'/h, y = y'/h, а h - некоторое вещественное число. Заметим, что случай h = 0 является особым. Всегда существует один набор однородных координат вида [х у 1]. Мы выбрали эту форму, чтобы представить координатный вектор [х y] на физической плоскости хy. Все остальные однородные координаты представляются в виде [hx hy h]. Данные координаты не сохраняют однозначности, например, все следующие координаты [6 4 2], [12 8 4], [3 2 1] представляют физическую точку (3,2).

Матрица преобразования для однородных координат имеет размер 3х3. В частности,

[T] =		a  b  0   c  d  0   m  n  1

где действие элементов а, b, с и d верхней части (2х2)-матрицы точно соответствует действиям, рассмотренным ранее. Элементы m и n являются коэффициентами перемещения в направлениях x и y соответственно. Полная двумерная матрица преобразования имеет вид

[x*  y*  1] = [x  y  1]		1  0  0   0  1  0   m  n  1		= [x+m  y+n  1]

Отметим, что каждая точка плоскости и даже начало координат x = y = 0 теперь могут быть преобразованы.

Пространственные преобразования

Точка в трехмерном пространстве [х  y  z] представляется четырехмерным вектором

[x'  y'  z'  h] = [x  y  z  1][T]

где [Т] является матрицей некоего преобразования. Как и ранее, преобразование из однородных координат в обычные задается формулой

[x*  y*  z*  1] =		x' h		y' h		z' h		1

Обобщенную матрицу преобразования размерности 4х4 для трехмерных однородных координат можно представить в следующем виде:

[T] =		a   b   с   p d   e   f   q g   i    j    r l   m   n   s

Матрицу преобразования 4х4 можно разделить на четыре отдельные части. Верхння левая (3x3)-подматрица задает линейное преобразование в форме масштабирования, сдвига, отражения и вращения. Левая нижняя (1х3)-подматрица задает перемещение, а правая верхняя (3х1)-подматрица - перспективное преобразование. Последняя правая нижняя (1х1)-подматрица задает общее масштабирование. Общее преобразование, полученное после применения этой (4 х 4)-матрицы к однородному вектору и вычисления обычных координат, называется билинейным преобразованием. В общем случае данное преобразование осуществляет комбинацию сдвига, локального масштабирования, вращения, отражения, перемещения, перспективного преобразования и общего масштабирования.