Лабораторная работа № 4:

" Построение кривых в форме Безье. Построение кривых в форме Фергюсона (Эрмита)"

Математические основы

Явный, неявный и параметрический вид задания функции.

Явный вид задания функции

у — f(x) - это явное выражение для у позволяет вычислять у при любом значении х (кроме описания вертикальных прямых , например, х=3 ) . Уравнение прямой линии у=2х+3 - пример явного задания функции.

Неявный вид задания функции

f(x,y)=0 - неявное задание функции от х и у.

Пример неявного задания функции - уравнение окружности х +у — 1 = 0 с радиусом г=1. Чтобы в этом случае получить явный вид задания функции, уравнение х + у - 1=0 надо разбить на два уравнения:

для верхней половины окружности получим у = + ( 1 - х ) для нижней - у = -(1+х)

Параметрический вид задания функции

В параметрическом виде задания функции х и у являются равноправными и представляются в виде функций от вспомогательного параметра t, то есть x = x(t),

У = У(0)

Параметрический вид, например, для уравнения окружности с радиусом г=1 будет записываться следующим образом:

X = COS t

У = sin t, где t лежит в интервале 0 < t < 2% .

Представление контуров в машинной графике

Наиболее распространены три типа представления контуров в машинной графике:

1. Кусочно-линейный

2. Линейно-круговой

3. Полиномиальный

Каждый из них имеет свои преимущества и свои недостатки.

1. Кусочно-линейный

По контуру кривой упорядоченно ( в порядке возрастания индекса !!! ) проставляются точки, которые затем соединяются отрезками прямых. В результате получаем массивы координат: xi,x₂,x₃, ,х„ и уьу₂,уз, ,Уп •

2. Линейно-круговой

Используется, как правило, в оборудовании с программным управлением, где контуры описываются с помощью отрезков и дуг окружностей. Название этого типа представления контуров говорит само за себя.

3. Полиномиальный

Явный вид задания полинома:

у = ао + ai_x + 32Х + + a_nxⁿ

Параметрический вид задания полинома:

х = а_Ох + aj_xt + a_2xt² + + a_nxtⁿ

у= ао_у + ai_yt + a2_yt² + ,... + a_nytⁿ

Переход от представления контура в виде параметрической кубической кривой к кусочно-линейному представлению

Используется для упрощения вычисления размеров контура, например, для вычисления длины контура, площади внутри контура и т.д.

При конструировании пространственных форм (этим занимается геометрическое моделирование) возникают задачи трёхмерного представления поверхностей в пространстве. Рассмотрим одно из наиболее широко распространённых представлений, а , именно, параметрические кубические полиномы. Итак, почему кубический полином ( то есть кривая описывается многочленом третьей степени )? Потому что кубический многочлен является параметрической функцией наиболее низкой степени, с помощью которой можно представить кривую, описывающую реальную пространственную кривую. Имеется много способов представления параметрических бикубических кривых. Рассмотрим один из них: кривые Безье .

Преимущество параметрических кубических кривых - нет разрывов.

Кривые Безье

Безье (1970) перегруппировал члены параметрического кубического многочлена Фергюссона и получил кривую следующего вида:

r= r(t) = (l-t)³po + 3t(l-t)²_Pl+3t²(l-t)p₂ + t³p3 ,

0<t<l

Ценность этой кривой в том, что для своего построения она требуют задания всего 4 точек. Две из четырех прямых, соединяющих эти четыре точки, будут являться касательными для кривой Безье и их взаимное расположение определяет форму кривой Безье.

Свойства кривой Безье

1. Кривая Безье является гладкой кривой.

2. Начинается в 1-ой вершине ро массива из четырёх точек р₀, pi, рг, рз, касается отрезка popi и заканчивается в последней точке р₃, касаясь отрезка ргРз-

3. Лежит в выпуклой оболочке, порожденной массивом точек р₀, pi, p₂, Рз-

4. Симметрична, то есть сохраняет свою форму при перемене порядка вершин массива на противоположный : р₀, р_ь р₂, Рз Рз, Рг, Рн Ро •

5. Если точки ро, pi, P2, Рз лежат на одной прямой , то кривая Безье совпадает с отрезком РоРз-

6. Если точки ро, pi, P2, Рз лежат в одной плоскости, то кривая Безье тоже лежит в этой плоскости.

7. Изменение положения хотя бы одной из четырёх опорных точек приводит к заметному изменению всей кривой Безье.

8. В уравнении, описывающем кривую Безье, нет свободных параметров - заданный набор из четырёх точек однозначно определяет кривую Безье, не давая возможности повлиять на её форму.

Кривые Безье

В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно).

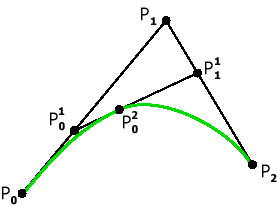
Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 8). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.

Рис. 1. Кривая Безье с 3 опорными точками.

Обозначим опорные точки как ,, начало кривой положим в точке (t=0), а конец в точке (t=1), для каждого найдем точку , таким образом, получим кривую второго порядка.

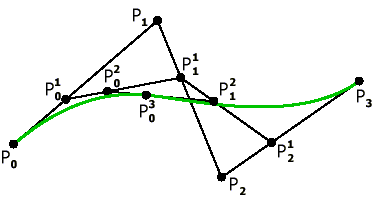
Теперь построим аналогичным методом кривую Безье с 4 опорными точками.

Рис. 2. Кривая Безье с 4 опорными точками.

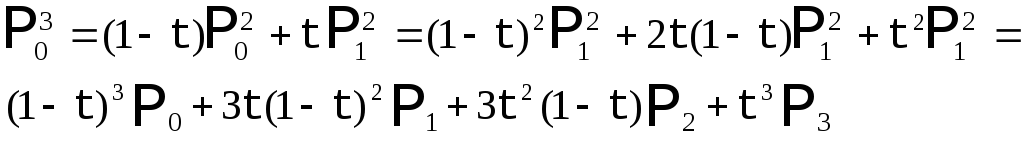
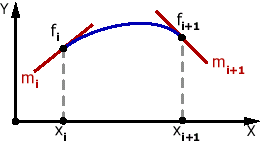
Кривые Фергюсона

Рис. 3. Кубическая интерполяция Эрмита.

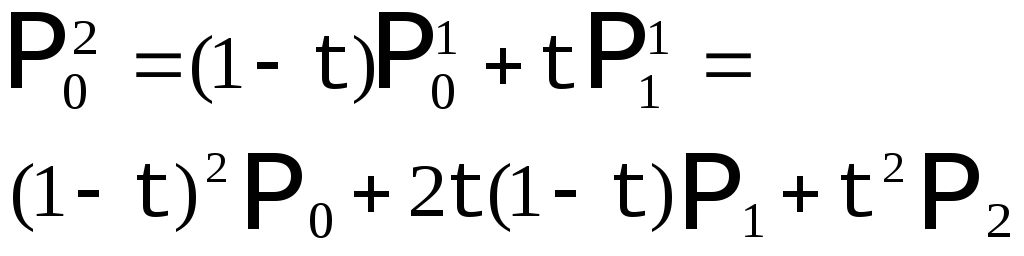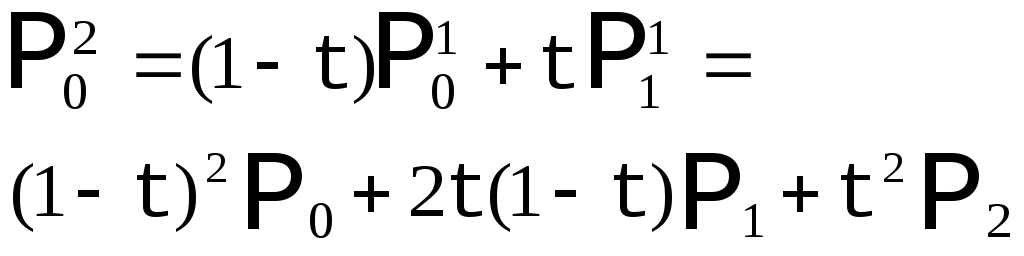
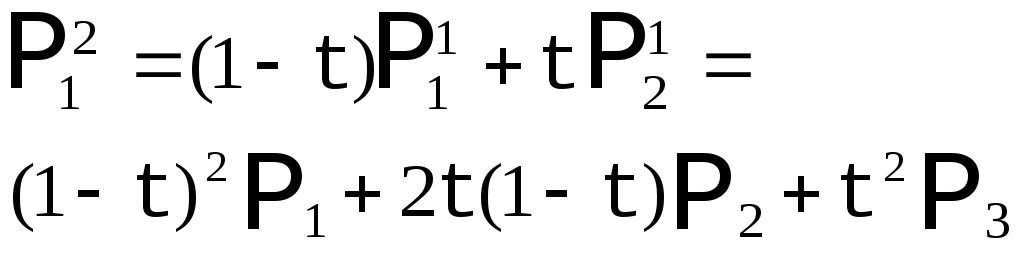
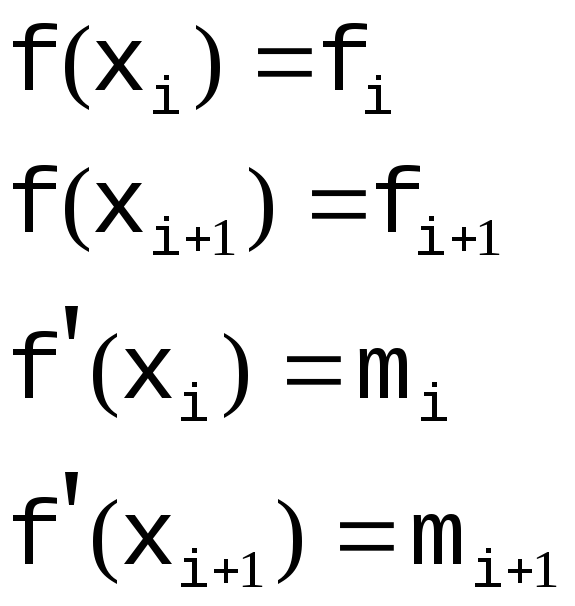Пусть заданы следующие условия: , тогда для каждого i будем искать искомую функцию в виде. Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно. Класс