
Уроки Физики / Кучеренко М. А. Стратегии смыслового чтения учебного текста по физике
.pdfЧитатель формулирует для себя вопросы «В чем особенность гармо-
нических колебаний? В чем заключается их особая роль?».
Далее выбирает основания для конкретизации элементов систематиза-
ции и выделения связи между ними:
1Что такое гармонические колебания?
2Какова особая роль гармонических колебаний в природе и технике?
3Общее условие гармоничности колебания?
4Примеры колебательных систем, в которых возникают гармониче-
ские колебания.
5 Виды представления гармонического колебания: график гармониче-
ских колебаний; векторная диаграмма гармонического колебания; представле-
ние гармонических колебаний в комплексной форме.
6 Постоянные величины, характеризующие гармонических колеба-
ния: амплитуда A, круговая (или циклическая) частота , частота , период
T , фаза колебаний Ф(t )= t + , начальная фаза .
7 Скорость при гармоническом колебательном движении.
8 Ускорение при гармоническом колебательном движении.
Сравнительная таблица как прием преобразования учебной информа-
ции эффективна в том случае, когда в мышлении читателя «перекрываются» некоторые важные аспекты рассматриваемого фрагмента действительности.
Примером такого рода фрагментов являются колебательные и волно-
вые процессы. При этом под процессом мы понимаем последовательную смену состояний системы.
Для создания сравнительной таблицы «Гармонические колебания и монохроматические волны» (см. стр. 237) использованы следующие источни-
ки:
1 Иродов, И.Е. Механика. Основные законы / И.Е.Иродов – М.: Лабо-
ратория базовых знаний, 2003.- 312 с.
221
2 Иродов, И.Е. Волновые процессы. Основные законы /И.Е.Иродов – М.: Лаборатория базовых знаний, 2001.- 256 с.
3 Белов, Д.В. Механика: учеб. пособие /Д.В.Белов – М.: Физический ф-т МГУ, НЭВЦ ФИПТ., 1998. – 144 с.
Основания для сравнения, с помощью которых выявляются качест-
венные и количественные особенности гармонических колебаний и монохро-
матических волн, перечислены ниже:
1Определение процесса.
2Примеры процессов в природе и технике.
3Что такое гармоническое колебание? Что такое монохроматическая
волна?
4Постоянные величины, характеризующие процесс.
5Графическое представление процесса.
6Кинематические величины, описывающие процесс.
7Уравнение, описывающее процесс.
Добавим, что необходимым условием успешной деятельности по соз-
данию таблиц различного вида является использование различных источни-
ков информации: учебников и учебных пособий, рекомендованных учебной программой дисциплины «Физика» или выбранных самостоятельно из пе-
речня учебников и учебных пособий для высшего профессионального обра-
зования; образовательных ресурсов Интернет; различных периодических из-
даний (научные и научно-популярных журналы); энциклопедий и энцикло-
педических словарей.
222
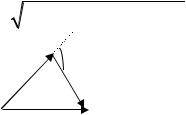
Таблица 2 - Обобщающая таблица «Законы сохранения в механике»
Какая |
Словесная |
|
Математи- |
При каких усло- |
Примеры проявления закона со- |
Следстви- |
В чем прояв- |
||||||||||||||||
физиче- |
формулиров- |
ческая |
за- |
вия |
сохраняет- |
хранения |
|
|
|
ем |
какого |
ляется свой- |
|||||||||||
ская ве- |
ка |
закона со- |
пись |
|
сяфизическая |
|
(в природе или технике) |
свойства |
|
ство |
|
про- |
|||||||||||
личина |
хранения |
фи- |
закона |
со- |
величина? |
|
|
|
|
|
|
|
простран- |
странства |
|||||||||
сохраня- |
зической |
ве- |
хранения |
|
|
|
|
|
|
|
|
|
|
|
|
ства |
|
и |
или времени, |
||||
ется? |
личины |
|
|
физической |
|
|
|
|
|
|
|
|
|
|
|
времени |
|
которое |
оп- |
||||
|
|
|
|
|
величины |
|
|
|
|
|
|
|
|
|
|
|
|
является |
|
ределяет |
со- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
закон |
со- |
хранение фи- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хранения |
зической |
ве- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
физической |
личины? |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величины? |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 Импульс |
Импульс |
|
|
|
Если сумма внеш- |
Движущаяся частица распалась на две |
Закон |
со- |
Пространство |
||||||||||||||
системы |
замкнутой |
|
P const. |
них сил равна ну- |
частицы с импульсами p1 и p , угол |
хранения |
|
однородно. |
|||||||||||||||
системы |
мате- |
лю Fi |
внешн |
0 |
между которыми |
равен . Для опре- |
импульса |
|
Это |
означает, |
|||||||||||||
матери- |
риальных |
то- |
|
|
|
|
вытекает |
из |
что |
в поведе- |
|||||||||||||
|
|
|
i |
|
|
|
деления импульса распавшейся части- |
||||||||||||||||
альных |
чек |
остается |
|
|
(система |
|
замкну- |
однородно- |
нии |
любой |
|||||||||||||
точек |
постоянным во |
|
|
тая). |
|
|
|
|
цы p, |
предполагая, что система замк- |
сти |
про- |
физической |
||||||||||
времени. |
|
|
|
|
|
|
|
|
нутая, |
воспользуемся законом сохра- |
странства. |
системы |
ни- |
||||||||||
|
Сохраняется |
|
|
Если |
сумма про- |
нения |
импульса: |
p = p1 + p2 . По- |
|
|
|
чего |
не изме- |
||||||||||
|
проекция |
им- |
Px const. |
екций |
внешних |
строим треугольник импульсов (см. |
|
|
|
нится, |
если |
||||||||||||
|
пульса |
на |
то |
сил |
на направле- |
рис) и по теореме косинусов опреде- |
|
|
|
эту |
систему |
||||||||||||
|
направление |
|
|
ние Ox равна ну- |
лим импульс распавшейся частицы: |
|
|
|
как целое по- |
||||||||||||||
|
(например, |
|
|
|
лю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
ступательно |
||||
|
|
|
|
|
|
|
|
p |
p2 |
p2 2p p cos |
|
|
|
||||||||||
|
Ox), |
на |
кото- |
|
|
|
|
|
|
|
|
|
|
сместить |
в |
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 2 |
|
|
|
|
|||||||
|
рое |
|
сумма |
|
|
|
внешн |
0 |
|
|
|
|
|
|
|
|
|
|
пространстве. |
||||
|
проекций |
|
|
|
F(i)x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ш |
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
||||||
|
внешних |
сил |
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|||||
|
равна нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
223
Продолжение таблицы 2
2 |
Закон |
Момент |
им- L const |
Если |
сумма мо- |
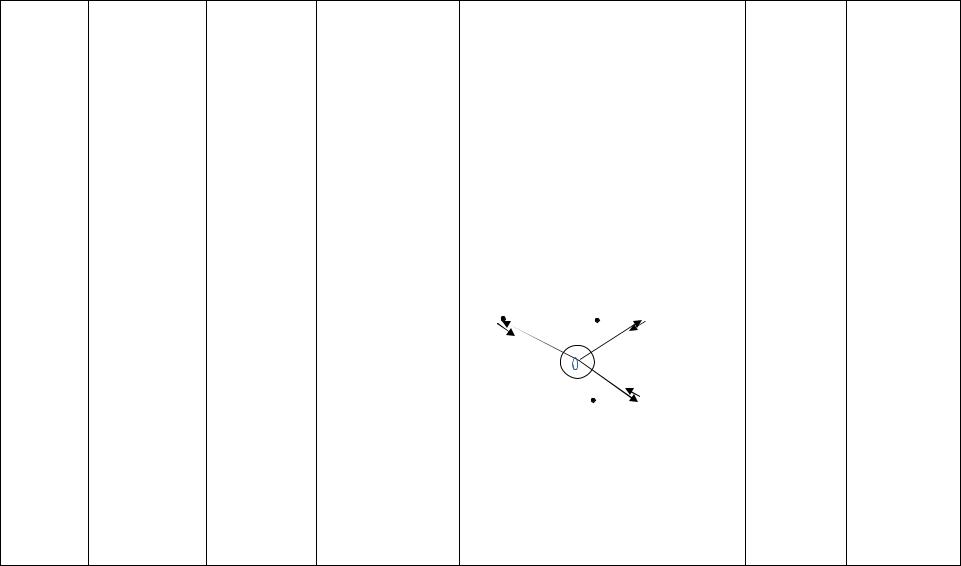
Момент импульса системы материаль- |
Закон |
со- |
Пространство |
|||||
сохране- |
пульса |
систе- |
ментов |
внешних |
ных точек, находящихся в централь- |
хранения |
|
изотропно. |
||||||
ния |
мо- |
мы материаль- |
сил (относительно |
ном поле сил, сохраняется, так как все |
момента |
|
Это |
означает, |
||||||
мента им- |
ных точек ос- |
той |
же |
точки) |
внешние силы направлены радиально к |
импульса |
|
что |
в поведе- |
|||||
пульса. |
тается |
|
посто- |
равна нулю: |
одной точке О (центру) |
или от нее. |
вытекает |
из |
нии |
любой |
||||
|
|
янным, |
если |
Mi 0. |
При этом момент каждой |
внешней си- |
изотропии |
физической |
||||||
|
|
сумма |
момен- |
лы Fi относительно центра равен ну- |
пространст- |
системы |
ни- |
|||||||
|
|
i |
|
|
||||||||||
|
|
тов |
внешних |
|
|
|
лю (поскольку угол i между радиу- |
ва. |
|
чего |
не изме- |
|||
|
|
сил |
(относи- |
|
|
|
|
|
нится, |
если |
||||
|
|
тельно той же |
|
|
|
сом-вектором ri и силой Fi равен ну- |
|
|
эту |
систему |
||||
|
|
точки) |
равна |
|
|
|
лю или 1800 ) и , следовательно, мо- |
|
|
как целое по- |
||||
|
|
нулю. |
|
|
|
|
|
|
|
вернуть |
в |
|||
|
|
|
|
|
|
|
|
мент импульса системы относительно |
|
|
пространстве. |
|||
|
|
|
|
|
|
|
|
центра сохраняется. |
|
|
|
|
|
|
m1 r |
|
|
r m2 |
|
1 |
|
2 |
F |
|
F1 |
|
|
|
2 |
|
|
|
|
|
|
M |
|
|
F3 |
|
|
|
||
|
|
|
||
|
|
r3 |
m3 |
|
|
|
|
||
224

Продолжение таблицы 2
3 Закон со- |
Механическая |
|
|
Если |
алгебраиче- |
хранения |
энергия замк- |
W W W |
ская |
сумма работ |
|
механиче- |
нутой системы |
k |
п |
всех внешних сил |
|
ской энер- |
частиц, в ко- |
const |
|
и всех внутренних |
|
гии |
торой нет дис- |
|
|
диссипативных |
|
|
сипативных |
|
|
сил равна нулю. |
|
|
сил, сохраня- |
|
|
|
|
|
ется в процес- |
|
|
|
|
|
се движения. |
|
|
|
|
|
|
|
|
|
|
При центральном упругом ударе дви- |
Закон |
со- |
Время |
одно- |
|||||||||||||||||
жущееся тело массой m1 ударяется о |
хранения |
родно. |
|
Это |
|||||||||||||||||
покоящееся |
тело массой m , в резуль- |
механиче- |
означает, |
что |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ской |
энер- |
в поведении |
|||||
тате скорость первого тела уменьшает- |
|||||||||||||||||||||
гии |
вытека- |
любой |
физи- |
||||||||||||||||||
ся в 2 раза. |
|
Для определения того, во |
ет |
из |
одно- |
ческой систе- |
|||||||||||||||
сколько раз масса первого тела больше |
|||||||||||||||||||||
родности |
мы ничего не |
||||||||||||||||||||
массы второго тела (n), воспользуемся |
|||||||||||||||||||||
времени. |
изменится, |
|
|||||||||||||||||||
законом сохранения импульса и зако- |
|
||||||||||||||||||||
|
|
|
если провести |
||||||||||||||||||
ном сохранения механической энергии |
|
|
|
||||||||||||||||||
|
|
|
в той же сис- |
||||||||||||||||||
(считаем систему из двух шаров замк- |
|
|
|
||||||||||||||||||
|
|
|
теме |
тот |
же |
||||||||||||||||
нутой; |
|
потенциальной |
энергией их |
|
|
|
|||||||||||||||
|
|
|
|
эксперимент в |
|||||||||||||||||
взаимодействия пренебрегаем): |
|
|
|
||||||||||||||||||
|
|
|
другое время. |
||||||||||||||||||
m1v1 = m1v1/ + m2v2// , |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
m |
1 |
v2 |
|
|
m |
1 |
v/ 2 |
|
m |
2 |
v |
// 2 |
|
|
|
|
|
|
|
||
|
1 |
|
= |
|
|
1 |
+ |
|
|
2 |
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
После |
|
математических |
преобразова- |
|
|
|
|
|
|
||||||||||||
ний получим n=3. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
m1 |
|
v |
m |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
// |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
v/ |
|
|
|
v2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
225
Таблица 3 - Систематизирующая таблица «Кинематика гармонических колебаний» |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основания для систематиза- |
|
|
|
|
|
|
|
|
Содержание учебной информации |
|||||
ции учебной информации |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Что такое гармонические |
Гармоническими называют колебания, в которых интересующая нас величина х (например, линейное |
|||||||||||||
колебания? |
или угловое смещение из положения равновесия) изменяется со временем t по закону |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
х Asin( t ) Acos( t ), |
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Какова особая роль гармо- |
а) В природе и технике часто встречаются колебания, близкие к гармоническим. |
|||||||||||||
нических колебаний в приро- |
б) Согласно теореме Фурье всякую периодическую функцию времени с периодом T можно предста- |
|||||||||||||
де и технике? |
вить как сумму гармонических колебаний с частотами, кратными частоте |
2 |
, и с соответствую- |
|||||||||||
|
|
|||||||||||||
|
щими значениями амплитуд и начальных фаз: |
|
|
T |
||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
х(t) а0 An sin(n t n ) |
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(a0 - постоянная, которая в большинстве задач не играет существенной роли). |
|||||||||||||
3 Общее условие гармонично- |
Если полная сохраняющаяся энергия системы выражается в виде квадратичной функции от не- |
|||||||||||||
сти колебаний. |
которой переменной и ее производной по времени, то собственными колебаниями этой системы явля- |
|||||||||||||
|
ются гармонические колебания: |
|
|
|
|
|
||||||||
|
|
|
2 |
|
m |
2 |
х |
2 |
|
|
|
|
|
|
|
|
mх |
|
|
|
|
сonst. |
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|||||
4 Примеры колебательных |
а) Вертикальный пружинный маятник: грузик массы m, подвешенный на невесомой пружине жестко- |
|||||||||||||
систем, в которых возника- |
стью k , совершающий вертикальные колебания под действием силы, направленной к положению рав- |
|||||||||||||
ют гармонические колеба- |
новесия и зависящей от смещения из этого положения линейно. |
|||||||||||||
ния. |
б) Математический маятник: материальная точка массы m, подвешенная на нерастяжимой нити дли- |
|||||||||||||
|
ной l, совершающая колебания в вертикальной плоскости под действием момента квазиупругой силы, |
|||||||||||||
|
направленной к положению равновесия и зависящей от смещения из этого положения линейно. |
|||||||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
226
Продолжение таблицы 3
5 Виды представления гармонического колебания: график гармонических колебаний; векторная диаграмма гармонического колебания; представление гармонических колебаний в комплексной форме.
а) Графический способ представления гармонического колебания
х |
|
|
A |
|
|
0 |
T 2 |
T t |
|
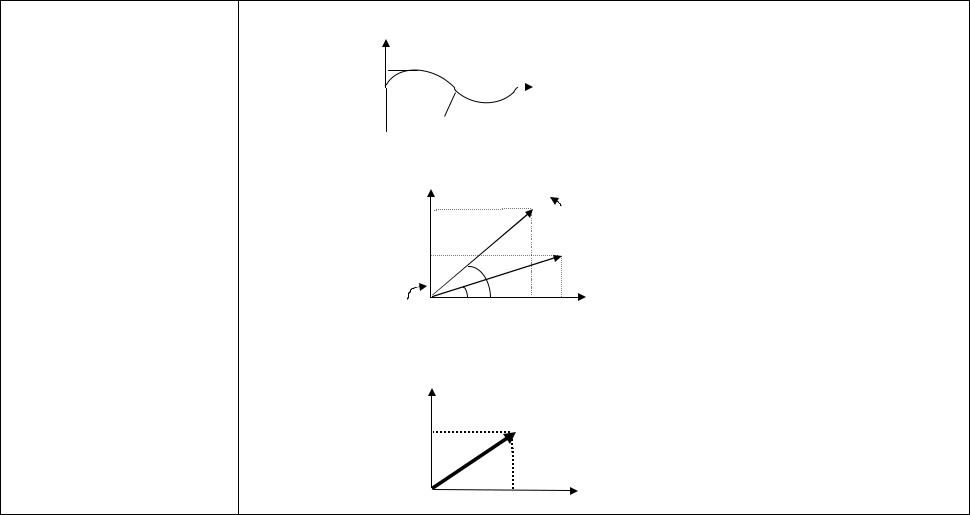
б) Векторная диаграмма гармонического колебания
y
|
|
A(t ) |
|
t + |
A(0 ) |
|
|
|
|
|
|
0 |
A cos( t + ) |
х |
A sin( t + ) |
|
|
в) Представление гармонических колебаний в комплексной форме
iy
Ae i( t+ )
A
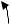 t +
t +
х
227

Продолжение таблицы 3
6 Постоянные величины, ха- |
Амплитуда A - максимальное значение колеблющейся величины. |
|||||||
рактеризующие гармониче- |
Круговая (или циклическая) частота - число колебаний, совершенное за 2 секунд. |
|||||||
ских колебания. |
Частота - число колебаний, совершаемых в единицу времени. |
|||||||
|
Период T - время одного полного колебания. |
|
|
|||||
|
Фаза колебаний Ф(t) t является аргументом синуса или косинуса в формуле гармониче- |
|||||||
|
ского колебания и характеризует стадию колебания. |
|
|
|
||||
|
Начальная фаза определяет значение фазы в момент времени t 0:Ф(0) . |
|||||||
|
|
|
|
|||||
7 Скорость при гармониче- |
Для материальной точки, совершающей колебание вдоль оси Ох скорость направлена вдоль |
|||||||
ском колебательном движе- |
оси Ох и равна: |
|
|
|
||||
нии. |
|
|
dх |
|
|
|
||
|
vх = |
|
|
= d( Asin t )/ dt = A cos t = vх0 sin( t + |
2). |
|||
|
dt |
|||||||
|
Скорость опережает координату по фазе на |
|
(по времени – на четверть периода). |
|||||
|
|
|
|
|
|
2 |
|
|
8 Ускорение при гармониче- |
Для материальной точки, совершающей колебание вдоль оси Ох ускорение направлена вдоль |
|||||||
ском колебательном движе- |
оси Ох и равно: |
|
|
|
||||
нии. |
aх |
d х |
d(A cos t)/ dt A 2 sin t aх sin( t ). |
|
||||
|
|
|
||||||
|
|
dt |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
Ускорение находится в противофазе с координатой.
228

Таблица 4 - Сравнительная таблица «Гармонические колебания и монохроматические волны»
|
Основания для сравнения |
Колебательный процесс |
|
|
|
Волновой процесс |
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
Колебаниями называют процессы, в которых одна |
При волновом процессе изменение некоторой физической |
|||||||
|
|
|
или несколько основных физических величин являются |
величины в какой-либо области пространства (возмущение |
|||||||
|
1 Определение процесса. |
периодическими или почти периодическими функция- |
(x, y,z,t)) |
не остается |
локализованным, а |
начинает |
|||||
|
ми времени |
|
|
|
распространяться с характерной для данных условий скоро- |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
стью. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Суточные и годовые колебания температуры на зем- |
Звуковые волны в жидких, твердых и газообразных средах |
|||||||
|
|
|
ле, электромагнитные колебания в колебательном кон- |
(роль возмущения играет скалярная физическая величина - |
|||||||
|
|
|
туре, колебания маятников (пружинного, математиче- |
небольшое |
переменное |
избыточное |
давление |
||||
2 Примеры процессов в природе |
ского, физического). |
|
|
|
p(t) p(x, y,z,t)), |
электромагнитные волны, |
распро- |
||||
и технике. |
|
|
|
|
|
страняющиеся в среде, и в вакууме (роль возмущения играют |
|||||
|
|
|
|
|
|
|
переменные напряженности электрического и магнитного |
||||
|
|
|
|
|
|
|
полей E(r,t)) и H(r,t)). |
|
|
||
|
|
|
|
|
|||||||
|
|
|
Гармонические колебания происходят по закону си- |
Монохроматические волны представляют собой распростра- |
|||||||
|
|
|
нуса или косинуса: |
|
|
|
нение гармонических колебаний. |
|
|||
|
|
|
|
|
|
Формула монохроматической волны, распространяющейся в |
|||||
|
3 Что такое |
гармоническое |
х(t) Asin( t ) Acos( t ), |
|
|
направлении оси Ox |
(возмущение распространяется в на- |
||||
|
2 |
|
|||||||||
|
колебание? Что |
такое моно- |
|
|
|
||||||
|
|
|
|
правлении Ox ) имеет вид: |
|
|
|||||
|
хроматическая волна? |
|
|
|
|
|
|
||||
|
|
|
|
|
(x,t) Asin( t kx ). |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
229

Продолжение таблицы 4
4 Постоянные |
величины, ха- |
1 |
x(t)-физическая величина, совершающая колебание; |
1 |
A- амплитуда волны, |
равная максимальному значению |
||||||||||
рактеризующие процесс. |
2 |
A-амплитуда колебания, равная максимальному |
колеблющейся величины; |
|
|
|
|
|
|
|||||||
|
|
значению колеблющейся величины; |
2 |
- круговая, или циклическая частота; число колебаний |
||||||||||||
|
|
3 |
- круговая, или циклическая частота; число коле- |
за 2 секунд; |
|
|
|
|
|
|
||||||
|
|
баний за 2 секунд; |
|
|
3 -частота, равная числу колебаний в единицу времени; |
|||||||||||
|
|
4 -частота, равная числу колебаний в единицу вре- |
4 T - период колебания; время одного полного колебания; |
|||||||||||||
|
|
мени; |
|
|
|
|
|
5 |
- начальная фаза, определяющая значение аргумента |
|||||||
|
|
5 T - период колебания; время одного полного колеба- |
гармонической функции в момент времени t 0; |
|||||||||||||
|
|
ния; |
|
|
|
|
|
6 |
- длина волны; путь, который проходит возмущение (со- |
|||||||
|
|
6 |
- |
начальная фаза, определяющая значение аргу- |
стояние с определенной фазой) за время. Равное периоду ко- |
|||||||||||
|
|
мента |
гармонической функции |
в момент времени |
лебаний T : T . |
|
|
|
|
|
|
|||||
|
|
t 0. |
|
|
|
|
|
7 |
k - волновое число: k |
2 |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 Графическое |
представление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
процесса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
(x,t ) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
T 2 |
T t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
o |
|
|
x |
|||
|
|
|
|
График гармонического колебания |
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
«Мгновенный профиль волны» |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
230
