
- •1. Понятие неопределённого интеграла
- •2. Свойство линейности. Простейшие интегралы
- •3. Подведение функции под знак дифференциала
- •4. Метод замены переменной в неопределённом интеграле
- •5. Интегрирование по частям
- •6. «Тригонометрические» интегралы
- •7. Интегрирование некоторых дробей
- •8. Универсальная тригонометрическая подстановка
- •9. Метод неопределённых коэффициентов
- •10. Интегрирование корней
- •11. Биномиальные интегралы
- •12. Решения и ответы

arctg(3  6x 1)dx – аналогичный мотив: замена 6x 1 t3 , и корня, как ни бывало.
6x 1)dx – аналогичный мотив: замена 6x 1 t3 , и корня, как ни бывало.
Решения этих и других примеров можно найти в статье Сложные интегралы.
И совсем редко встречается интеграл вида n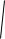 cxax db dx , который решается заменой
cxax db dx , который решается заменой
ax b t n . Конкретный пример тоже есть в указанном выше источнике. cx d
11.Биномиальные интегралы
Снекоторыми из них мы уже имели дело, и сейчас пришло время систематизировать информацию. Так называемый биномиальный интеграл имеет
следующий вид: xm (a bxn ) p dx . Он берётся в трёх случаях.
1) Случай первый. Самый лёгкий.
Если степень p – целое число.
|
|
|
|
|
|
|
|
Например: |
|
|
xdx |
|
|||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
(1 |
|
|
x ) |
||||
|
|
|
|
||||
Представим интеграл в стандартном виде (это лучше делать на черновике):
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
xdx |
|||||||||
|
|
|
|
x 2 |
(1 x5 ) 2 dx |
|||||||
|
|
|
|
|
|
|
||||||
|
|
5 |
|
|
|
2 |
||||||
(1 |
|
|
x ) |
|||||||||
|
|
|
|
|
|
|
|
|
||||
Мы видим, что степень p 2 – целая, а, значит, действительно имеет место
первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в только что рассмотренных Примерах 81, 82, поэтому приводить почти такие же решения особого смысла нет. Я просто покажу, какую замену здесь нужно провести.
Смотрим на знаменатели дробей:
Выписываем знаменатели: 2, 5. Находим наименьшее общее кратное этих чисел. Очевидно, это 10: оно делится и на 2 и на 5, кроме того – десятка самая маленькая в этом смысле.
После замены x t10 все корни гарантировано пропадут. Решать этот пример не нужно, поскольку я его придумал с ходу и легко там не будет =)
© Емелин А., http://mathprofi.ru, Высшая математика – просто и доступно! |
65 |
|

2) xm (a bxn ) p dx – случай второй |
|
||
Если |
m 1 |
– целое число, то необходимо провести замену a bxn t N , где |
N – |
|
|||
|
n |
|
|
знаменатель дроби p . |
|
||
Спокойствие, только спокойствие, сейчас во всём разберемся. |
|
||
Пример 83

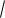 x2 1dx x
x2 1dx x
Во-первых, представим интеграл в стандартном виде xm (a bxn ) p dx :
|
|
|
|
|
|
|
1 |
|
|
|
x |
2 |
1dx |
|
|||
|
|
x 1(x2 1)2 dx . Вообще говоря, формально правильнее было записать |
||||||
|
|
x |
||||||
|
|
|
|
|
|
|
||
1
x 1 ( 1 x2 )2 dx , но перестановка слагаемых в скобках не играет никакой роли.
Выписываем степени:
m 1, n 2 , p 12
И сразу проверяем, не относится ли наш интеграл к первому случаю?
p 12 – целое? Нет.
Проверяем второй случай:
m 1 |
|
1 1 |
|
0 |
0 |
– целое, значит у нас второй случай, и согласно правилу, |
||
n |
|
2 |
2 |
|||||
|
|
|
|
|||||
нужно провести замену a bxn t N , где N – знаменатель дроби p .
В рассматриваемом примере p 12 , и знаменатель этой дроби равен «двойке».
Таким образом, «наше всё» – это замена: x2 1 t 2 .
! Несмотря на то, что она очевидна: 
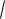 x2 1
x2 1 
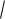 t2 t , строго следуйте алгоритму решения биномиального интеграла! Ибо не всё очевидное правильно ;)
t2 t , строго следуйте алгоритму решения биномиального интеграла! Ибо не всё очевидное правильно ;)
Оформляем решение:
© Емелин А., http://mathprofi.ru, Высшая математика – просто и доступно! |
66 |
|
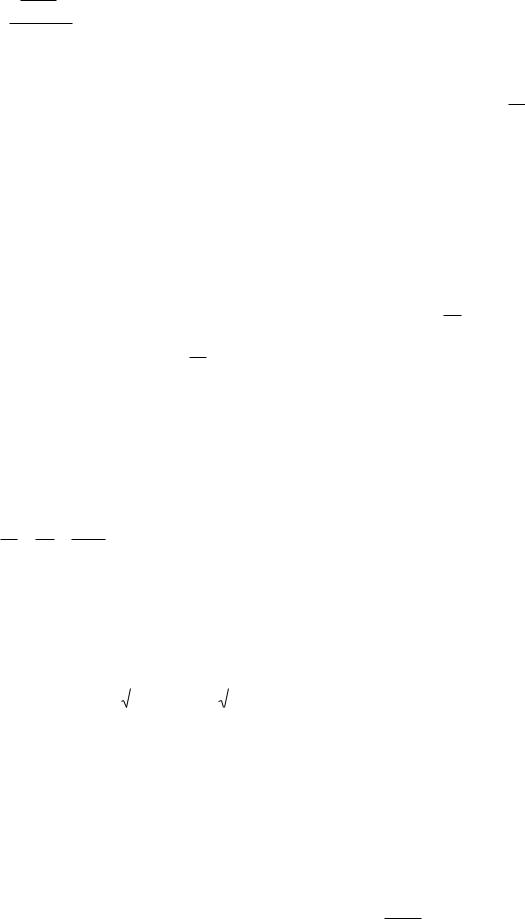

 x2 1dx (*) x
x2 1dx (*) x
Итак, в результате замены x2 1 t 2 корень у нас исчезает, и теперь нужно выяснить, во что превратится оставшаяся часть подынтегрального выражения: dxx .
Берём нашу замену x2 1 t 2 и навешиваем на обе части значки дифференциала: d (x2 1) d (t2 )
после чего оба дифференциала раскрываем:
(x2 1) dx (t 2 ) dt 2xdx 2tdt
xdx tdt
Но вот, незадача, тут получилось xdx, а нам-то нужно выразить dxx . Да без проблем – умножаем обе части на x12 :
xdx |
1 |
tdt |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
x2 |
|
|
|
|
|
|
|
||
Таким образом: |
|
dx |
|
tdt |
. Уже лучше, но нам надо выразить |
dx |
только через t , а |
|||
|
|
|
|
|||||||
|
x |
x2 |
x |
|||||||
вправой части есть «икс» в квадрате. Что делать? Снова вспоминаем нашу замену
x2 1 t 2 , выражаем из неё нужный нам x2 t 2 1. Окончательно:
dxx tdtx2 t 2tdt1 .
Несколько головоломно, но, увы, другие алгоритмы еще запутаннее. Собственно, продолжаем решение:
(1) |
|
t tdt |
(2) |
|
|
t 2dt |
(3) |
|
(t2 |
1 |
1)dt |
(4) |
|
|
|
|
1 |
|
(5) |
|||||
(*) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dt |
||
t 2 1 |
t 2 1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
t2 1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
t2 1 |
|
||||||||||||||
|
|
|
|
|
(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t arctgt C |
x2 |
1 |
arctg |
|
x2 1 C, |
где C const |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
(1)Проводим подстановку согласно замене.
(2)Записываем компактно числитель.
(3)Уже без комментариев :)
(4)Делим числитель на знаменатель.
(5)Интегрируем по таблице.
(6)Проводим обратную замену: если x2 1 t 2 , то t 
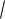 x2 1
x2 1
© Емелин А., http://mathprofi.ru, Высшая математика – просто и доступно! |
67 |
|
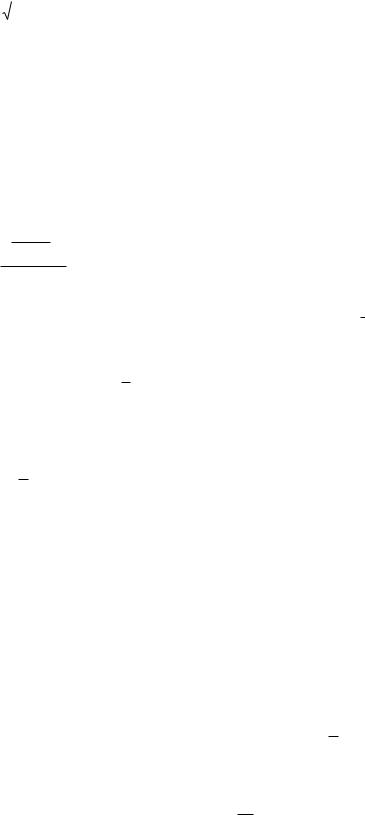
Пример 84 |
|
|
|
|
|||||||
|
|
x3dx |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
x2 4 |
|
|
|
|
|||||||
Это пример для самостоятельного решения. |
|
|
|||||||||
3) xm (a bxn ) p dx – случай третий. Самый сложный. |
|
|
|||||||||
Если |
m 1 |
|
p |
– целое число, то необходимо провести замену b |
a |
t N , где |
|||||
n |
xn |
||||||||||
|
|
|
|
|
|
||||||
N – знаменатель дроби p .
Пример 85

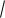 x2 4dx
x2 4dx
x2
1
Представим интеграл в стандартном виде x 2 (x2 4)2 dx и выпишем степени и
коэффициенты:
m 2 , n 2 , p 12 , a 4 , b 1
1) Не относится ли наш интеграл к первому случаю?
p 12 – целое? Нет.
2) Проверяем второй случай:
|
m 1 |
|
2 1 |
|
1 |
|
– целое? Нет. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
n |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) |
m 1 |
p |
2 1 |
|
1 |
|
1 |
|
1 |
|
0 |
– целое! Значит, у нас третий случай. |
|||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
n |
|
2 |
|
|
2 |
2 |
2 |
|
|
|
|
|
|||||
И, согласно правилу, здесь нужно провести замену b |
a |
t N , где N – |
|||||||||||||||||
xn |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
знаменатель дроби p . В рассматриваемом примере p 12 , и знаменатель этой дроби равен опять же «двойке». Коэффициенты (будьте внимательны) a 4 , b 1
Таким образом, искомая замена: 1 x42 t 2
Оформляем решение:
© Емелин А., http://mathprofi.ru, Высшая математика – просто и доступно! |
68 |
|

 x2 4dx (*)
x2 4dx (*)
x2
Проведём замену 1 x42 t 2 и сразу разберёмся с корнем. Это труднее, чем в предыдущих случаях.
Сначала из нашей замены 1 x42 t 2 нужно выразить «икс квадрат»:
|
4 |
t 2 1 x2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x2 |
t 2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теперь подставляем x2 |
|
|
4 |
|
под корень: |
|
|
|
|
|
|||||||||||||||||||||||||
t |
2 1 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 4t2 |
|
|
|
|
4t2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2t |
|
||||||||||
|
|
x2 4 |
|
|
4 |
|
|
|
|
– от корня мы пока не |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
t2 1 |
|
|
|
|
|
|
t2 1 |
t2 |
1 |
|
|
t2 1 |
|
|||||||||||||
избавились, по это только пока ;) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
На втором этапе выясняем, во что превратится оставшаяся часть |
|||||||||||||||||||||||||||||||||||
подынтегрального выражения |
|
dx |
. Берем нашу замену 1 |
4 |
t 2 и навешиваем |
||||||||||||||||||||||||||||||
|
x2 |
x2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
дифференциалы на обе части: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d 1 |
|
|
|
d (t |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вот тут-то уже не самая простая производная:
(1 4x 2 ) dx 2tdt
(0 4 ( 2)x 3 )dx 2tdt
4dx tdt
x3
теперь слева по правилу пропорции вычленяем нужный нам кусок: dxx3 14 tdt
dxx2 14 txdt
Опять проблема, в правой части у нас есть x , а нам нужно всё выразить через t .
Берём ранее найденный x2 |
|
4 |
|
|
и выражаем |
x |
|
|
4 |
|
|
|
|
2 |
|
|
||||||||||||||||||||||
|
t 2 1 |
t 2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
t 2 1 |
|||||||||||||
Окончательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dx |
1 |
txdt |
1 |
t |
|
2 |
|
dt |
|
|
tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x2 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
t 2 1 |
2 |
t 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2t |
|
|
|
dx |
|
|
tdt |
|
|
|
|
|||||||||||||||||||
В итоге мы выразили |
|
x2 4 |
|
|
|
|
|
|
|
и |
|
|
|
|
(смотрим вверх на |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 1 |
|
|
2 t 2 |
1 |
|
|
|
|
|
|
|
|
|||||||||||
исходный интеграл!), и всё готово для продолжения решения:
© Емелин А., http://mathprofi.ru, Высшая математика – просто и доступно! |
69 |
|

(*) |
|
|
|
2t |
|
|
|
|
|
|
|
tdt |
|
|
|
|
|
|
t |
2 |
dt |
|
|
(t |
2 |
1 1)dt |
|
1 |
|
|
1 |
|
dt |
|||||||||||||||||||||||||||||
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
1 |
|
|
|
|
|
|
t |
2 |
1 |
|
|
|
|
|
t |
2 |
1 |
|||||||||||||||||
|
|
|
t |
2 |
|
1 |
|
|
2 t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2 |
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t 1 |
|
|
(4) |
|
|
|
4 x2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||||
dt |
|
|
|
|
|
|
|
|
t |
|
ln |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
C |
|
|||||||||||||||||||||||||
t 2 1 |
|
2 |
t 1 |
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
x |
2 |
|
1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
4 x2 |
|
|
|
1 |
|
ln |
|
|
4 x2 |
x |
C, |
где C const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 x2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(1)Проводим подстановку согласно замене.
(2)Упрощаем выражение и выносим «минус» за знак интеграла (так удобнее).
(3)Разваливаем интеграл на 2 части и, понятно, интегрируем.
(4)Проводим обратную замену. В третьем случае биномиального интеграла это
тоже труднее. Если изначально 1 |
4 |
t 2 , то t2 |
x2 4 |
t |
|
x2 4 |
|
|
|
x2 4 |
|
. |
x2 |
x2 |
x2 |
|
|
||||||||
|
|
|
|
|
|
|
x |
|||||
(5) Избавляемся от четырехэтажности в логарифме.
Пример 86
|
|
dx |
|
|
|
|
|
|
|
|
|
(x2 1)3 |
|
Это пример для самостоятельного решения (здесь m 0 ). Полное решение и ответ только для выживших читателей =)
Что делать, если биномиальный интеграл xm (a bxn ) p dx не подходит ни под один из рассмотренных случаев? Это грустный четвертый случай, когда интеграл не берётся.
Поздравляю! Теперь Вы сможете решить почти любой интеграл!
Почти. Студентам-технарям настоятельно рекомендую проработать неоднократно упоминавшуюся статью Сложные интегралы, в частности, метод сведения интеграла к самому себе. Я намеренно не включил в данный курс «раритеты», поскольку его целью была именно быстрая помощь, и надеюсь, что этой цели мне удалось достичь.
Дополнительную информацию по теме однократных интегралов можно найти в соответствующем разделе портала mathprofi.ru (ссылка на аннотацию к разделу).
Из учебной литературы рекомендую: К.А. Бохан, 1-й том (попроще),
Г.М. Фихтенгольц, 2-й том (посложнее), Н.С. Пискунов (для ВТУЗов).
Желаю успехов!
© Емелин А., http://mathprofi.ru, Высшая математика – просто и доступно! |
70 |
|
