
- •Росжелдор
- •«Сибирский государственный университет путей сообщения» (сгупс)
- •Устройство и ремонт железнодорожного пути
- •Краткая рецензия
- •Оглавление
- •Введение
- •1 Определение класса пути. Выбор конструкции верхнего строения пути
- •1.1 Определение кода железнодорожного пути
- •1.2 Выбор конструкции верхнего строения пути
- •1.3 Установление схемы ремонтов пути и разработка календарного графика их проведения
- •1.4 Выводы по первому разделу
- •Определение основных размеров обыкновенного стрелочного перевода, укладываемого в стесненных условиях
- •2.1 Расчетная геометрическая схема стрелочного перевода
- •2.2 Расчет основных параметров и разбивочных размеров обыкновенного стрелочного перевода, укладываемого в стесненных условиях
- •2.2.1 Расчет радиуса переводной кривой, длины прямой вставки, малых и больших полуосей стрелочного перевода
- •2.2.2 Определение ординат для разбивки переводной кривой стрелочного перевода
- •2.2.3 Определение длин рельсов соединительной части стрелочного перевода
- •2.3 Установление ширины колеи
- •2.4 Выводы к разделу
- •Организация работ по очистке станционных путей от снега
- •3.1. Определение объема снега, подлежащего уборке
- •3.2 Определение продолжительности очистки станции от снега
- •3.3 Выводы по разделу
- •Заключение
- •Список использованных источников
- •Приложение 1
- •Приложение 2
2.2 Расчет основных параметров и разбивочных размеров обыкновенного стрелочного перевода, укладываемого в стесненных условиях
2.2.1 Расчет радиуса переводной кривой, длины прямой вставки, малых и больших полуосей стрелочного перевода
По заданию необходимо уменьшить длину типового перевода на величину , мм, равное 470 мм. Так как укорочение составляет более 250 мм, следует выполнить перерасчет его основных параметров и разбивочных размеров. Характеристики стрелочного перевода приведены в таблице П1.1, приложения П1.
Теоретическая длина стрелочного перевода Lту, мм, с учетом уменьшения его длины на , определяется по формуле:
Lту = Lп – m1 – p – ; |
(2.1) |
Lту = 31035 – 2765 – 2090 – 790 = 25390 мм.
При этом практическая длина стрелочного перевода Lпу, мм, после его укорочения станет равной:
Lпу = Lп – ; |
(2.2) |
Lпу = 31035 – 790 = 30245 мм.
Спроецировав контур ABC (рисунок 2.1) на вертикальную и горизонтальную оси, получаем систему уравнений:
|
(2.3) |
где S0 – ширина колеи по прямому направлению стрелочного перевода, мм, равная 1520 мм;
Ry – радиус переводной кривой по рабочей грани упорной нити стрелочного перевода после укорочения его длины, мм;
– длина прямолинейного остряка, мм;
α – угол между рабочими гранями крестовины, рад.;
βп – полный стрелочный угол, рад;
d – прямая вставка, мм;
yo – ордината в корне остряка, мм.
Решив систему уравнений, укороченный радиус переводной кривой Ry и длина прямой вставки d определятся по формулам 2.4 и 2.5:
|
(2.4) |
|
(2.5) |
Угол между рабочими гранями крестовины α, рад, определяется по формуле:
α = arctg(1/N), |
(2.6) |
где N – знаменатель марки крестовины.
α = arctg(1/9) = 0,110657 рад.
Полный стрелочный угол определяется по формуле:
|
(2.7) |
βп = 0,0079488 + (8300/300000) = 0,035616 рад.
Ордината корня остряка вычисляется по формуле:
yo
=
Ro(cos |
(2.8) |
yo = 300000(0,999968 – 0,999366) = 181 мм.
Длина прямого рамного рельса зависит от длины остряка, переднего и заднего вылетов, а также от принятого типа корневого крепления:
lpp = m1 + l‘o + m2, |
(2.9) |
Проекция криволинейного остряка на рамный рельс l′o, мм, вычисляется по формуле:
l′o = R0(sinβп – sinβн); |
(2.10) |
l′o = 300000(0,0356085 – 0,0794872) = 8298 мм.
Тогда задний вылет рамного рельса определяется по формуле:
m2 = lpp – l′o – m1; |
(2.11) |
m2 = 12500 – 8298 – 2765 = 1437 мм.
Таким образом, укороченный радиус переводной кривой Ry и длина прямой вставки d составят:
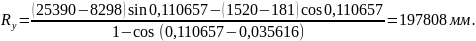
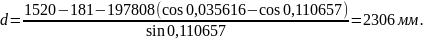
Малые полуоси стрелочного перевода b0 и a0, мм, согласно расчетной схемы (рисунок 2.1) определяются по формулам:
|
(2.12) |
|
(2.13) |
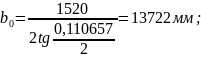
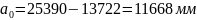 .
.
Соответственно большие полуоси:
a = a0 + m1; |
(2.14) |
b = b0 + p; |
(2.15) |
a = 11668 + 2765 = 14433 мм;
b = 13722 + 2090 = 15812 мм.
За стрелочным переводом на биссектрисе угла α устанавливается предельный столбик. Расстояния, определяющие положения предельного столбика, определяются по формулам:
g = e/2; f = 4100N ; |
(2.16) |
где e – расстояние между осями путей в месте установки предельного столбика, мм, равное 4100 мм;
g, f – расстояния от предельного столбика соответственно до оси пути и центра перевода, мм, (рисунок 2.2).
g = 4100/2 = 2050 мм;
f = 41009 = 36900 мм.
Расстояние от математического центра крестовины МЦ до предельного столбика определяется по формуле:
|
(2.17) |
f1 = 25809 = 23220 мм.
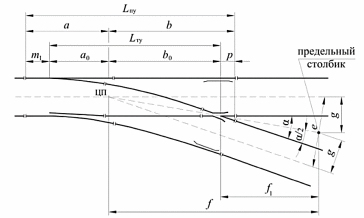
Рисунок 2.2 – Схема стрелочного перевода с основными и осевыми размерами и предельным столбиком

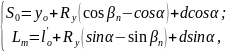
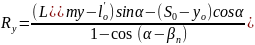 ;
;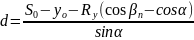
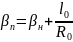 ;
;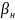 – cosβп);
– cosβп);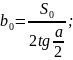
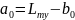 ;
;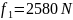 ;
;