10.Б Построим график закона распределения вероятностей отклика декодера:

Законы распределения вероятностей отклика декодера и отклика квантователя очень близки по форме, т.е. принятый сигнал декодируется корректно с требуемым отношением сигнал/шум h₀².

11. Полагая фнч на выходе цап приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:

Рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПП), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП).

СКПП:

ССКП:

ОСКП:

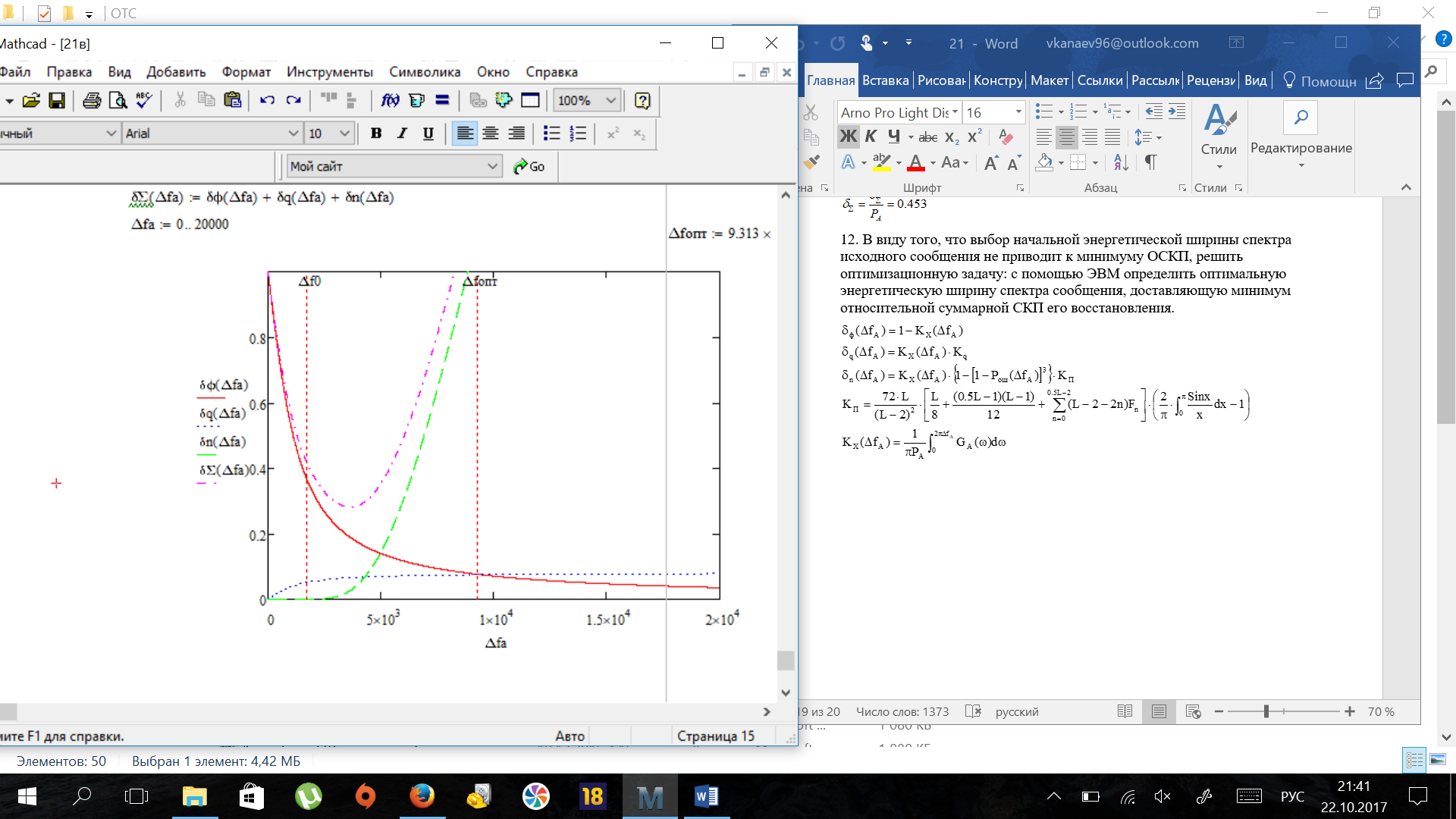
12. В виду того, что выбор начальной энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу: с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления.

Выводы:

В смешанной системе связи сообщения передаются с искажениями, которые возникают при фильтрации, квантовании двоичном и L-ичном ДКС

ОСКП получилась большая. Чтобы ее уменьшить, необходимо увеличить число уровней квантования. Тогда и уровень шума квантования будет уменьшаться, а спектр сигнала в канале – расширяться. Шум квантования уменьшить можно неравномерным квантователем.

Список использованной литературы:

1. В.Г. Санников - Методические рекомендации по выполнению курсовой работы-М.:1996.

2. Конспект лекций.