8.Б Построим в масштабе графики:

Построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП.

ФПВ:

Огибающая гауссовской помехи распределена по закону Релея:

ФПВ аддитивной смеси гармонического сигнала и узкополосной гауссовской помехи:

ФПВ огибающей принимаемого сигнала подчиняется обобщенному распределению Рэлея (распределение Райса):

9. Учитывая, что используется некогерентный метод детектирования сигнала, рассчитаем:

9.А Среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС:

За количественную меру помехоустойчивости в системах электросвязи принимают среднюю на бит вероятность ошибки:

При равенствах априорных вероятностей р(0) = р(1) = 0.5, а также условных вероятностей р(1/0) = р(0/1) = р_ош (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна р_ош.ср = р_ош

Скорость передачи информации по двоичному симметричному ДКС:

Показатель эффективности системы передачи:

9.Б Изобразим схему приёмника сигналов и опишем принцип его работы, поясним случаи, когда он вносит ошибки: Приемник сигналов дчм

сигнал дискретной модуляции

помеха (шум) в НКС

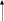
ВУ

Детектор, представляющий собой линейную систему с переменными параметрами, схема детектора состоит из перемножителя и ФНЧ, прошедшего полосовой фильтр с эффективной полосой пропускания равной к детектору подводятся опорный сигнал и перемножается с принятым, после чего оба перемноженных сигнала поступают на вычитающее устройство, далее сигнал поступает на дисретизатор к которому подводится последовательность дискретизирующих импульсов с периодом , которые необходимы для взятия отсчета в середине посылки длительностью . В РУ (решающем устройстве) отсчеты сравниваются с пороговым напряжением и принимается решение - передана 1, если , или передан 0, если . Под действием помех в канале связи амплитуда сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0.

10. Рассматривая отклик декодера пру как случайный дискретный сигнал на входе l – ичного дкс:

10.А Рассчитаем распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по L – ичному ДКС, относительные потери в скорости передачи информации по L – ичному ДКС:

Распределение вероятностей дискретного сигнала на выходе детектора:

n	0	1	2	3	4	5	6	7
Pпринn		0.023	0.1357	0.3379	0.3379	0.1357	0.02305

Энтропия ошибочных решений:

Энтропия восстановленного L-ичного сигнала:

Скорость передачи информации по L-ичному ДКС:

Относительные потери в скорости: