
573
.pdf
|
̇ ̇ |
|
̈ |
̈ |
̇ |
|
После сокращения на m2l2 ≠ 0 уравнение принимает такой вид:
̈+ ̈ |
̇ |
+ g |
|
Таким образом, нелинейная система двух дифференциальных уравнений Лагранжа записывается как
|
̈ |
|
̈ |
̇ |
{ |
|
|
||
̈ |
̈ |
|
̇ |
|
|
|
|||
|
|
|
Если считать углы α1(t), α2(t) малыми, то колебания маятников вблизи нулевого положения равновесия можно описать линейной системой уравнений. Чтобы получить такую систему, вернемся назад к исходному лагранжиану системы:
L=T V= |
̇ |
̇/2+ |
̇ ̇ |
+ |
+ g |
|
|
|
|
Запишем этот лагранжиан в более простом виде. Разложим косинусы, входящие в него, в ряд Маклорена и сохраним лишь линейные и квадратичные члены:
С учетом малости величин произведения ̇ ̇и квадратов величин углов α1, α2 в разложении косинусов, можно ограничиться линейным слагаемыми. Подставляя это в исходный лагранжиан и учитывая, что потенциальная энергия определяется с точностью до константы, получим лагранжиан двойного маятника в виде:
231

|
̇ |
|
|
̇+ |
̇ ̇ |
|||
L=T V= |
|
|
|
|
||||
g |
/2+ |
|||||||
|
|
|
|
|||||
|
|
|
|
|||||
Выведем дифференциальные уравнения Лагранжа для данного лагранжиана, которые записываются в таком виде:
|
|
|
, |
|
|
|
|
|
. |
̇ |
|
|
|
̇ |
|
||||
|
|
|
|
|
|
||||
После нахождения частных производных и несложных преобразований получаем систему двух дифференциальных уравнений Лагранжа:
̇̇
{
̇̇
или
{ |
̈ |
̈ |
|
̈ |
̈ |
||
|
Данную систему уравнений можно записать в компактной матричной форме. Введем матрицы
( |
) |
( |
), |
( |
|
) |
( ) |
Тогда система дифференциальных уравнений представляется в виде
M̈
Вслучае одного тела такое уравнение описывает свободные незатухающие колебания с определенной частотой. В случае двойного маятника решение будет содержать колебания с двумя характерными частотами, которые называются
232

нормальными модами. Нормальные моды представляют собой действительную часть комплекснозначной векторной функции
( |
) |
[( ) |
] |
где H1, H2 − собственные векторы, ω − действительная частота. Значения нормальных частот ω1, 2 определяются из решения характеристического уравнения
det(K M)=0.
Выведем общие формулы для циклических частот ω1, 2 в случае произвольных масс m1, m2 и длин l1, l2:
| |
| |
, |
|
| |
|
|
|
|=0, |
|
( |
|
) ( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
+ |
|
|
|
|
( |
) + |
= 0. |
Мы получили биквадратное уравнение для частот ω. |
|||||
Вычислим дискриминант: |
|
|
|||
D=m2(l1+l2)2g2 |
|
4m1mg2l1l2=g2m[m(l1+l2)2 |
4m1l1l2]. |
||
Таким образом, квадраты нормальных частот ω1, 2 равны
√
или
233
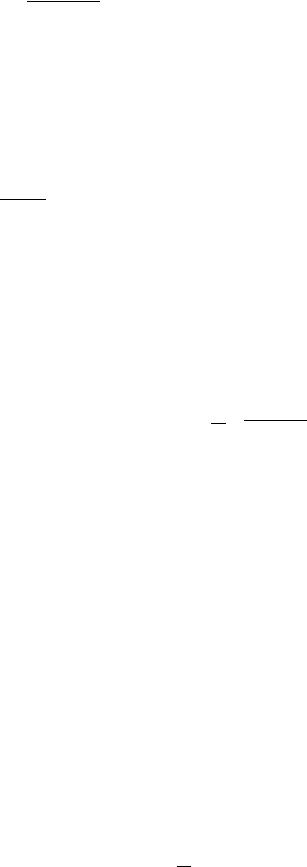
, |
√ |
|
- |
Данное выражение является несколько громоздким. Поэтому далее рассмотрим случай, когда длины стержней обоих маятников равны: l1 = l2 = l. Тогда нормальные частоты будут определяться более компактной формулой
[2lm √ |
|
|
= |
|
|
|
|
|
= |
|||
√ |
|
|
|
√ |
||||||||
|
||||||||||||
= |
|
|
|
, где |
|
|
. |
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||
Как видно, собственные частоты ω1, 2 зависят лишь от отношения масс μ = m2/m1. Зависимости частот ω1, ω2 от параметра μ (при условии /l = 1) показаны выше на рисунке 3. В частности, при равных массах m1 = m2 = m, т.е. при μ = 1, собственные частоты равны
|
|
|
√ |
|
√ |
|
|
|
|
|
|
|
|
|
|
√ |
|
||||||
|
|
|
|
|
|||||||
Общее решение системы дифференциальных уравне- |
|||||||||||
ний (1) записывается в виде |
|
|
|
|
|
|
|
|
|||
|
( |
) = Re[( |
)exp(i )]= |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
= ( √ |
|
) |
|
|
|
|
|
(√ |
|
), |
|
|
|
|
|
|
|
|
|
|
|||
где постоянные C1, C2, φ1, φ2 |
зависят от начальных положе- |
||||||||||
ний и скоростей маятников. |
|
|
|
|
|
|
|
|
|||
Рассмотрим характер малых колебаний для некоторого конкретного набора начальных данных. Пусть, например, координаты и скорости маятников в начальный момент имеют
такие значения:
̇ ̇
234

В этом случае начальные фазы равны нулю: φ1 = φ2 = 0. Определим постоянные C1 и C2:
{ |
√ |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
C1 = - C2, 2C2√ |
|
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C 2 |
|
|
√ |
|
|
, C1 |
|
|
√ |
|
|
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Тогда закон колебаний маятников выражается форму- |
|||||||||||||||||||||||||||||
лами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где циклические частоты ω1,ω 2 определяются соотношением
√ |
|
√ |
√ |
|
|
√ |
|
√ |
√ |
|
|
|
, |
|
. |
||||||||
|
|
||||||||||
Здесь углы α1(t), α2(t) выражаются в радианах, а время t в секундах. На рисунках 4-6 приведены графики малых коле-
баний маятников для трех значений μ: μ1 = 0.2, μ2 = 1, μ3 = 5,
при l = l1 = l2 = 0.25 м, g = 9.8 м/c2.
Углы отклонения маятников для удобства приведены в градусах. Из графиков видно, что в системе происходят биения, при которых энергия циклически переходит от одного маятника к другому. Когда один маятник почти останавливается, другой раскачивается с максимальной амплитудой. Через некоторое время маятники "меняются ролями" и так далее. Колебания с большей частотой ω1 модулируются более низкочастотными колебаниями с частотой ω2. Это особенно хорошо заметно на рисунке 6 при большом значении μ (μ3 = 5), когда разница между частотами ω1 и ω2 велика.
235
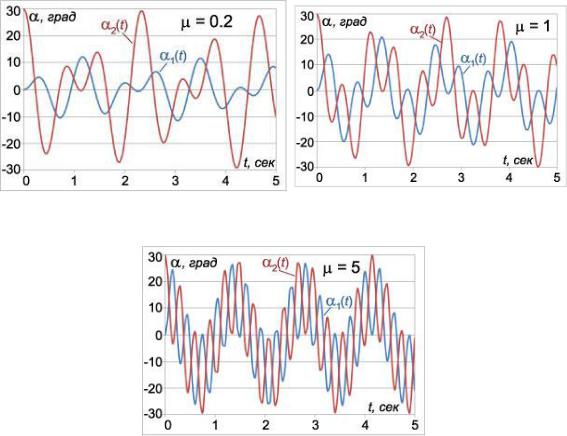
Рис. 4. Зависимость углов α1, α2 |
Рис. 5. Зависимость углов α1, α2 |
от времени t при μ1 = 0.2 |
от времени t при μ2 = 1 |
Рис. 6. Зависимость углов α1, α2 от времени t при μ = 5
Итак, малые колебания двойного маятника имеют периодический характер и описываются суммой двух гармоник с частотами ω1, ω2, зависящими от параметров системы. Характерным свойством малых колебаний двойного маятника является эффект биений.
Наиболее распространенным методом численного решения дифференциальных уравнений является метод РунгеКутты. Различные вариации этого метода используются в большинстве математических пакетов (MatLab, Maple, Mathematica, Mathcad), как правило, с автоматическим контролем точности и адаптивным временным шагом.
Для численного моделирования движения двойного маятника воспользуемся вычислительными средствами универсальной компьютерной системы «Mathematica». Предварительно несколько упростим дифференциальные уравнения
236
(11.31), полагая, что длины маятников одинаковы: l1 = l2 = l. Введем также параметр μ, равный отношению массы второго маятника к массе первого: μ = m2/m1. Тогда система уравнений (11.31) принимает следующий вид:
|
̈ |
̈ |
̇ |
|
{ |
|
|
||
̈ |
̈ |
̇ |
|
|
|
|
|||
|
|
|
||
с начальными условиями: |
, ̇(0) = |
̇(0) = |
||
|
|
|
1 |
2 |
0 и где введено обозначение |
. |
|
||
|
Описанная модель реализована для различных значений |
|||
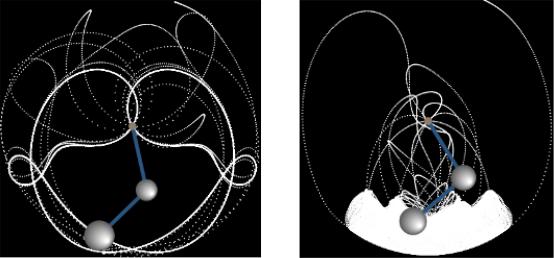
параметров α0 и μ в виде анимации, фрагменты которой приведенной ниже. Для упрощения начальные углы отклонения маятников приняты равными: α1 = α2 = α0. Данное приложение наглядно демонстрирует хаотическую динамику двойного маятника при различных значениях параметров μ и . Интересно, что в некоторых режимах в системе возникают устойчивые траектории, как, например, на рисунке 7, или компактные области притяжения, как на рисунке 8.
Рис. 7. Устойчивые траектории |
Рис. 8. Компактные области |
|
притяжения траекторий |
||
двойного маятника |
||
двойного маятника |
||
при μ = 2.75, α = 161° |
||
при μ = 1.28, α = 158° |
||
|
||
|
237 |
Заключение
Моделирование систем и процессов, исследование различных явлений на моделях стало одним из основных методов изучения сложных технических систем. Существующий аппарат современной математики, мощные средства вычислительной техники, развитые компьютерные технологии обработки информации позволяют успешно решать любые практические задачи, стоящие перед обществом.
Тема моделирования и разработки математических моделей процессов, явлений, объектов, систем весьма многогранна. В данном учебном пособии рассмотрены лишь некоторые основные формы математических моделей и пути разработки этих моделей. Изучение приведенных здесь материалов можно рассматривать как первый шаг в область современного математического моделирования технических систем.
238
Контрольные вопросы к разделам
Раздел 1.
1.1Моделирование как метод исследования.
1.2Правила моделирования.
1.3Этапы моделирования.
1.4Понятие модели.
1.5Классификация моделей.
1.6Классификация математических моделей.
1.7Свойства математических моделей.
1.8Требования к математическому моделированию.
1.9Этапы построения и применения математических моделей.
Раздел 2.
2.1Понятие системы.
2.2Принципы системного подхода.
2.3Классификация систем.
Раздел 3.
3.1Техника.
3.2Технический объект.
3.3Жизненный цикл технического объекта.
3.4Техническая система.
3.5Технология.
3.6Взаимосвязь техники и технологии
Раздел 4.
4.1Методология проектирования.
4.2Техника и технические объекты с позиций системного подхода.
4.3Структура и параметры объектов проектирования.
4.4Стадии, аспекты и режимы процесса проектирования.
4.5Постановка задач проектирования.
4.6Особенности технологии автоматизированного проектирования технического объекта.
Раздел 5.
5.1Кинематика:
5.2Динамика материальной точки.
239
5.3Две основные задачи динамики материальной точки.
5.4Дифференциальные уравнения движения материальной точки.
Раздел 6.
6.1Связи.
6.2Действительные возможные перемещения.
6.3Число степеней свободы, идеальные связи.
6.4Общие теоремы динамики системы материальных точек.
6.5Теорема о движении центра масс механической системы.
6.6Случай замкнутой механической системы.
Раздел 7.
7.1Примеры несвободных систем.
7.2Принцип виртуальных перемещений.
7.3Применение принципа виртуальных перемещений.
7.4Принцип Даламбера.
7.5Принцип Даламбера - Лагранжа.
7.6Общее уравнение механики.
7.7Уравнения Лагранжа в независимых координатах.
Раздел 8.
8.1Размерные и безразмерные величины.
8.2Основные и производные единицы измерения.
8.3О формуле размерности.
8.4О втором законе Ньютона.
8.5Структура функциональных связей между физическими величинами.
8.6Параметры, определяющие класс явлений.
Раздел 9.
9.1Метод обобщенных переменных.
9.2Теоремы подобия.
Раздел 10.
10.1Особенности экспериментальных факторных моделей.
10.2Принципы планирования эксперимента.
10.3План эксперимента.
10.4Регрессионный анализ.
240
