пр 4, Стешенко (екон)

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ БІОРЕСУРСІВ І ПРИРОДОКОРИСТУВАННЯ УКРАЇНИ

Кафедра економетрики

Практичне заняття 4

«Економетричні моделі динаміки»

Виконала студентка 3 курсу 1 групи

Економічного факультету

Стешенко Тетяна Олександрівна

Київ - 2023

Практична робота 4. Економетричні моделі динаміки

Варіант 21

Одним із основних завдань аналізу рядів динаміки є виявлення основної тенденції розвитку соціально-економічних явищ. Під загальною тенденцією динамічного ряду розуміють тенденцію до зростання, зниження або стабілізації рівня будь-якого явища.

Одним з найпростіших прийомів виявлення тенденції розвитку є прийом укрупнення періодів.

Ковзна середня згладжує варіацію рівнів, але не дає ряду динаміки, в якому всі вихідні рівні були б замінені вирівняними. Це пояснюється недоліком вирівнювання ряду способом ковзної середньої, при якому вирівняний ряд “скорочується”, порівняно з вихідним, на члена з одного та з другого кінця (під розуміють кількість членів, з яких визначають ковзні середні).

Прагнення в процесі вимірювання ряду замінити всі рівні вирівняними зумовлює застосування досконаліших прийомів вирівнювання рядів динаміки. До таких прийомів належать: вирівнювання за середнім абсолютним приростом, середнім коефіцієнтом зростання і способом найменших квадратів.

В основі застосування способу вимірювання ряду динаміки за середнім абсолютним приростом лежить припущення , що кожен наступний рівень змінюється, порівняно з попереднім, приблизно на однакову величину, що дорівнює середньому абсолютному приросту.

Рівняння, яке відображає тенденцію розвитку явища за цим способом вирівнювання ряду динаміки, має такий вигляд:

,

де - вирівняні рівні ряду динаміки; - початковий рівень ряду динаміки; - середній абсолютний приріст; 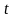- порядковий номер дати .

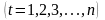Вирівняний за середнім абсолютним приростом ряд динаміки на графіку – це пряма лінія, яка з’єднує два крайніх вирівняних рівні (мінімальне і максимальне значення). Недолік вирівнювання за цим способом полягає у ому, що розрахунок спирається лише на два крайніх значення ряду, які зазнають випадкових коливань.

Вирівнювання ряду динаміки за середнім коефіцієнтом зростання застосовують тоді, коли в досліджуваному ряду кожен наступний рівень змінюється, порівняно з попереднім, приблизно в ту саму кількість разів, що дорівнює величині середнього коефіцієнту зростання.

Вирівняні значення рівнів ряду динаміки визначаються за формулою:

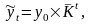
де - середній коефіцієнт зростання.

На графіку вирівняний ряд динаміки зображують як показникову криву, яка з’єднує початковий і кінцевий рівні динаміки. Цей спосіб вирівнювання, який спирається на два крайніх значення, має ті самі недоліки, що і вирівнювання за абсолютним приростом.

Досконалішим і точнішим прийомом вирівнювання рядів динаміки, який враховує всі рівні вихідного ряду, є аналітичне вирівнювання способом найменших квадратів. Вирівнювання цим способом ґрунтується на припущенні, що зміни досліджуваного ряду динаміки можна наближено виразити певним математичним рівнянням (функцією, що апроксимується), за яким і визначають вирівняні рівні динамічного ряду. Іншими словами, рівні ряду динаміки розглядають як функцію часу, де - рівні динамічного ряду, визначені за відповідним рівнянням на момент часу .

Аналітичне вирівнювання можна провести з використанням різних типів функцій: прямої лінії, параболи другого порядку, функції кривої (експоненти), гіперболи тощо.

Рівняння, що виражає рівні ряду динаміки як деяку функцію часу , називається трендом.

Суть аналітичного вирівнювання динамічних рядів полягає в тому, що фактичні рівні ряду змінюють рядом рівнів, які змінюються плавними рівнями, обчисленими на основі певної кривої, вибраної в припущенні, що вона найточніше відображає загальну тенденцію явища.

Вирівнювання динамічних рядів способом найменших квадратів, як і вирівнювання за допомогою інших прийомів, має здійснюватися в межах одноякісних періодів. Якщо в динамічному ряді є якісно специфічні періоди, то виявляти тенденцію доцільно в межах кожного з них.

Залежно від вихідних даних для вирівнювання рядів динаміки можна вибрати різні типи кривих або пряму лінію. Аналіз динаміки соціально – економічних явищ свідчить, що їх зміна супроводжується абсолютними приростами, які постійно зростають і зменшуються, постійним темпами зростання і приросту, прискорення або уповільнення, тобто їх вирівнювання слід здійснювати за рівнянням прямої лінії, параболи другого порядку або показникової кривої.

Вирівнювати динамічні ряди за рівнянням прямої лінії доцільно тоді, коли для емпіричного ряду характерні більш або менш постійні ланцюгові абсолютні прирости, тобто оді, коли рівні ряду змінюються приблизно в арифметичній прогресії. Стосовно рядів динаміки аналітичне вирівнювання прямої лінії має такий вигляд:

де - вирівняні значення рівнів динамічного ряду; - час, тобто порядкові номери періодів; і - параметри рівняння шуканої прямої; - початок відліку (економічного змісту не має), - коефіцієнт регресії або пропорційності, який показує середній щорічний приріст (зниження) явища, які вивчають (тангенс кута нахилу прямої лінії до осі абсцис).

Параметри і шуканої прямої, що задовольняють вимозі способу найменших квадратів, знаходять, розв’язуючи таку систему рівнянь:

де - число рівнів динаміки.

Техніка утворення системи рівнянь така. Перше рівняння отримують множенням усіх членів вихідного рівняння на коефіцієнт при (на одиницю) і підсумовування знайдених добутків. Щоб мати друге рівняння, всі члени вихідного рівняння слід помножити на коефіцієнт при (на ) і знайдені добутки підсумувати. Аналогічно будують систему нормальних рівнянь і для інших кривих (параболи другого порядку, гіперболи тощо).

Розрахунок параметрів рівняння ( і ) можна значно спростити, якщо відлік часу ( ) здійснювати так, щоб сума показників часу дорівнювала нулю . Цього досягають так. Рівень, що перебуває в середині ряду динаміки приймають за умовний початок відліку, або нульове значення. Для того, щоб сума показників часу дорівнювала нулю, умовні позначення потрібно додавати так: а) при непарному числі рівнів ряду динаміки, щоб одержати 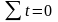рівень, який перебуває в середині ряду, прирівнюють до нуля, а рівні, розташовані вище його, позначають числами із знаком мінус –1, -2, -3 і т.д., а нижче числами із знаком плюс (+1,+2,+3 і т.д.), б) при парному числі рівнів ряду динаміки рівні, що лежать вище серединного значення (воно перебуває в середині між двома середніми датами), позначають натуральними числами із знаком мінус (-1, 3, -5 і т.д.), а рівні, що лежать нижче серединного значення, - натуральними числами із знаком плюс (+1, +3, +5 і т.д.).

За умови, що , система нормальних рівнянь спрощується, набуваючи такого вигляду:

Звідки:

; .

Розв’язуючи вихідну систему нормальних рівнянь способом визначників, параметри і можна обчислити за іншими формулами:

.

При аналізі рядів динаміки доводиться стикатися з такими випадками, коли в рядах немає даних про їх рівні за певний період. Такі дані можуть бути відсутні, або всередині ряду, чи на початку, чи в кінці його.

Приблизне значення відсутніх рівнів усередині одноякісного періоду, коли невідомим є рівні, що лежать по обидві сторони невідомого, називають інтерполяцією ряду динаміки. Приблизне визначення невідомих рівнів, що лежать за його межами, тобто в майбутньому (або минулому), називають екстраполяцією ряду динаміки. Відповідно, екстраполювання може здійснюватися в бік майбутнього (перспективна екстраполяція), так і в бік минулого (ретроспективна екстраполяція). Щоб мати досить надійні результати обчислення відсутніх рівнів, інтерполяцією та екстраполяцією слід проводити в межах однорідних періодів, яким властива однакова закономірність розвитку.

Інтерполяцію та екстраполяцію можна здійснювати різним способами. Най простішим є використання середніх характеристик досліджуваного ряду динамки: середнього абсолютного приросту (при стабільних ланцюгових абсолютних приростах) і середнього коефіцієнта зростання (при стабільних темпах зростання). Однак визначення відсутніх рівнів ряду динаміки, зокрема при екстраполяції, найчастіше пов’язують з аналітичним вирівнюванням рядів способом найменших квадратів, який дає найточніші результати.

Дослідження динаміки суспільних явищ і виявлення основної тенденції їхнього розвитку в минулому створюють основу для їхніх майбутніх розмірів.

Екстраполяція відіграє важливу роль у плануванні. Вона дає змогу прогнозувати соціально-економічні явища. Прогнозування є важливим етапом планової роботи.

Прогнозування – це процес наукового виявлення можливих шляхів і результатів майбутнього розвитку соціально-економічних явищ, оцінка показників. Що характеризують ці явища для більш або менш віддаленого майбутнього. Розрізняють короткострокові прогнози (від кількох днів до одного року), середньострокові (від одного року до 5 років) і довгострокові (понад 5 років).

Застосування екстраполяції для прогнозування ґрунтується на припущенні, що характер динаміки. Тобто певна закономірність (тенденція) зміни досліджуваного явища яка спостерігається в певному періоді часу в минулому, збережеться на обмеженому відрізку в майбутньому.

На основі даних про динаміку врожайності зернових культур в окремих господарствах області за 2006 – 2020 рр. визначити:

1. Здійснити згладжування ряду динаміки, застосувавши способи укрупнення періодів і ковзну середню.

2. Здійснити вирівнювання ряду динаміки способом найменших квадратів згідно з рівнянням прямої лінії коли та та охарактеризувати параметри рівняння.

3. Здійснити прогнозування врожайності на перспективу на основі аналітичного вирівнювання ряду динаміки способом найменших квадратів на 2006 – 2020рр.

Таблиця 1. Динаміка врожайності зернових культур в господарствах за 2006 – 2020 рр.

Рік	Врожайність, ц/га	Ковзна середня
		суми по ковзних п’ятиріччях	середні по ковзні п’ятиріччях
2006	16	-	-
2007	22	-	-
2008	19	109	21,8
2009	24	123	24,6
2010	28	133	26,6
2011	30	150	30
2012	32	163	32,6
2013	36	172	34,4
2014	37	181	36,2
2015	37	189	37,8
2016	39	-	-
2017	40	-	-

Таблиця 2. Розрахункові дані для аналітичного вирівнювання динамічного ряду урожайності зернових культур за лінійним трендом

Рік	Урожайність ц
					Вирівняна урожайність, ц					Вирівняна урожайність, ц
2006	16	1	1	16	22,695		-6	36	-96	24,36986
2007	22	2	4	44	24,023		-5	25	-110	25,30822
2008	19	3	9	57	25,351		-4	16	-76	26,24658
2009	24	4	16	96	26,68		-3	9	-72	27,18493
2010	28	5	25	140	28,008		-2	4	-56	28,12329
2011	30	6	36	180	29,336		-1	1	-30	29,06164
2012	32	7	49	224	30,664		0	0	0	30
2013	36	8	64	288	31,992		1	1	36	30,93836
2014	37	9	81	333	33,321		2	4	74	31,87671
2015	37	10	100	370	34,649		3	9	111	32,81507
2016	39	11	121	429	35,977		4	16	156	33,75342
2017	40	12	144	480	37,305		5	25	200	34,69178
Разом	360	78	650	2657	360		-6	146	137	354,3699

Дані табл. 1 показують, що в господарствах проявляється тенденція до підвищення врожайності зернових.

,

Невідомі параметри 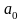і визначають способом найменших квадратів, розв’язуючи систему нормальних рівнянь:

Підсумкові дані табл. 2 перенесемо в систему рівнянь з двома невідомими параметрами:

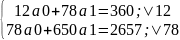
Розділивши кожне рівняння на коефіцієнти при , тобто перше – на 12, друге – на 78 матимемо:

Від другого рівняння віднімаємо перше:

1,8а1 = 4,1282

а1 = 4,1282/1,8 = 1,3282

Щоб визначити параметр , підставимо в одне з проміжних рівнянь значення параметрів :

а0+6,5*1,3282 = 30

а0 = 30 – 8,6333 = 21,3667

Отже, рівняння прямої, яке характеризує динаміку урожайності зернових в господарстві матиме такий вигляд:

Yt = 21,3667+1,3282t

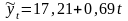
Це означає, що у 2005 р., тобто році який передує досліджуваному періоду, вирівняна урожайність зернових становила 21,3667 ц, початкова швидкість підвищення врожайності – 1,3282 ц.

12a0 = 360

a0 = 360/12 = 30

146a1 = 137

a1 = 137/146 = 0,938356

Отже, рівняння прямої, яке характеризує динаміку урожайності зернових в господарстві матиме такий вигляд:

Yt= 30+0,938356t

Це означає, що у 2005 р., тобто році який передує досліджуваному періоду, вирівняна урожайність зернових становила 30 ц, початкова швидкість підвищення врожайності – 0,94 ц.