НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ БІОРЕСУРСІВ І ПРИРОДОКОРИСТУВАННЯ УКРАЇНИ

Кафедра економетрики

Практичне заняття 9

«Побудова економетричної моделі на основі системи одночасних структурних рівнянь»

Виконав студент 3 курсу 1 групи

Економічного факультету

Касяненко Максим Андрійович

Київ - 2023

Практична робота 9. Побудова економетричної моделі на основі системи одночасних структурних рівнянь

Завдання. На основі вихідних даних наведених у прикріпленому файлі (табл. 1-10), виконати такі дії:

1) нехай необхідно побудувати економетричну модельна основі системи одночасових структурних рівнянь 

Y1t=a12X1t + a13X2t+ u1t

Y2t=b21Y1t+a21X1t+a23X3t + a24X4t+u2t

Y1t- фондомісткість, гр.од., Y2t-продуктивність праці, гр.од.-ендогенні змінні;

X1t - коефіцієнт плинності, % X2t - рівень втрат робочого часу, % X3t-середній стаж, років , X4t - заробітна плата, гр.од.-екзогенні змінні.

2) визначити ідентифікованість кожного рівняння;

3) які методи доцільно використовувати для оцінки параметрів кожного рівняння.

Варіант 9

Таблиця 9

Місяць	Продуктив ність праці, гр.од.	Заробіт на плата, гр.од.	Фондомісткість, гр. од.	Коефіцієнт плинності, %	Рівень втрат робочо го часу, %	Серед ній стаж, років
1-й	64	225	30	12,0	15,0	8,0
2-й	65	230	35	11,5	14,3	8,5
3-й	62	210	33	11,0	12,0	7,0
4-й	63	230	34	10,0	12,8	9,0
5-й	66	250	36	9,0	13,0	10,0
6-й	67	250	38	8,0	12,5	11,0
7-й	69	255	40	7,5	11,0	9,5
8-й	64	235	41	7,2	11,5	12,0
9-й	72	240	45	7,0	10,0	10,0
10-й	73	242	45	4,5	9,0	14,0
11-й	74	245	46	4,0	8,0	12,5
12-й	76	246	48	3,7	7,5	12,0
13-й	77	250	47	3,6	6,5	10,0
14-й	82	255	50	3,0	6,0	11,0
15-й	79	251	49	3,1	6,2	12,0
16-й	84	260	51	3,2	5,8	15,0
17-й	85	265	50	3,5	5,5	15,5
18-й	87	266	53	3,0	5,0	14,5
19-й	85	260	55	3,0	4,5	14,0
20-й	89	265	56	2,0	4,7	15,0
21-й	90	270	57	3,0	5,0	15,0
22-й	91	270	58	4,0	5,1	16,5
23-й	90	271	58	4,0	4,8	15,7
24-й	92	275	60	5,0	5,2	15,8

Розв’язання

Запишемо умову ідентифікованості структурних рівнянь:

,

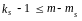де — кількість ендогенних змінних, які входять в -те рівняння;

–– кількість екзогенних змінних, які входять в -те рівняння;

— загальна кількість екзогенних змінних.

Для першого рівняння:

k_s = 1; m_s = 2; m = 4

Звідси k_s – 1 ≤m – m_s 1 -1 ˂ 4 – 2 0 ˂ 2, тобто рівняння системи є надідентифікованим.

Для другого рівняння:

k_s = 2; m_s = 3; m = 4

Звідси k_s –1≤m – m_s 2 -1 = 4 –3 1=1 тобто друге рівняння системи є точно ідентифікованим.

Зважаючи на те, що перше рівняння моделі є надідентифікованим, для оцінки його параметрів можна використати метод 2МНК.

Друге рівняння моделі є точно ідентифікованими, тому для оцінки параметрів цих рівнянь можна використати як метод 2МНК, так і НМНК. Обидва методи дають однакові оцінки параметрів моделі.