7.4. Метод золотого сечения

В основу метода положено разбиение отрезка неопределенности [a;b] в соотношении золотого сечения, такого, что отношение длины его большей части ко всей длине отрезка равно отношению длины его меньшей части к длине его большей части:

l

l₂ l₁

Положим l =1, тогда l₂² = 1 - l₂ , а l₂² + l₂ -1= 0, откуда

где k₁, k₂ - коэффициенты золотого сечения.

В методе золотого сечения каждая точка (х₁ и х₂)осуществляет золотое сечение отрезка.

или

Геометрическая интерпретация метода золотого сечения приведена на рис. 7.4-1.

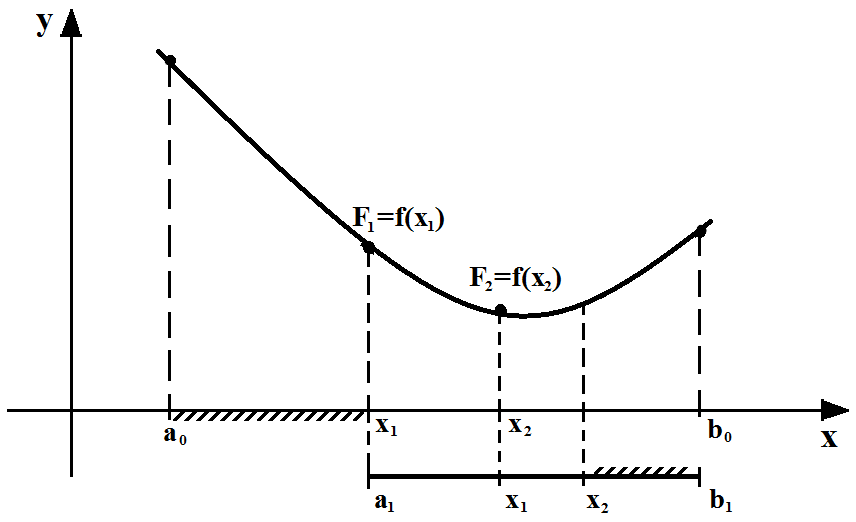
Рис. 7.4-1.

Нетрудно проверить, что точка х1 осуществляет золотое сечение не только отрезка [a;b], но и отрезка [a;х₂]. Точно так же точка х₂осуществляет золотое сечение не только отрезка [a;b], но и отрезка [х₁;b]. Это приводит к тому, что значение целевой функции на каждой итерации (кроме первой) вычисляется один раз.

После каждой итерации длина отрезка неопределенности сокращается в 1.618 раза. Длина конечного отрезка неопределенности D_n = 0.618ⁿD₀, где D₀= (b-a) – начальная длина отрезка.

Условие окончания процесса итераций Dn e. Отсюда можно найти количество итераций, необходимое для достижения точки минимума:

Отсюда поэтому, логарифмируя, получим

Пример 7.4-1. Пусть минимум функции f(x) = x³ – x + e^-x отделен на отрезке [0;1]. Определить количества итераций и конечные длины отрезков неопределенности, необходимые для достижения заданных точностей e=0.1 и e=0.01.

Таблица 7.4-1

N	a	b	x1	x2	f(x1)	f(x2)	Dn
1	0	1	0.38196	0.61803	0.35628	0.15704	0.61803
2	0.38196	1	0.61803	0.76393	0.15704	0.14772	0.382
3	0.61803	1	0.76393	0.85410	0.14772	0.19462	0.236
4	0.61803	0.85410	0.70820	0.76393	0.13953	0.14772	0.146
5	0.61803	0.76393	0.67376	0.70820	0.14188	0.13953	0.090

При e = 0.1 x*=0.718847, f(x*)=0.139925.

При e = 0.01 x*=0.704139, f(x*)=0.139516.

7.5. Метод средней точки

Алгоритм метода средней точки основан на сокращении длины текущего отрезка неопределенности [a;b], путем отбрасывания его части, не содержащей точки минимума. Как известно, для того чтобы на отрезке [a;b] существовал минимум, необходимо, чтобы первая производная на нем была неубывающей. Выбирается пробная точка, принадлежащая отрезку (как правило, середина отрезка c=(a+b)/2), и если , то в следствии унимодальности функции точка минимума не может лежать левее точки с, а если , то не может лежать правее точки с.

Пусть на отрезке [a;b] отделен единственный минимум функции f(x). Требуется определить значение точки минимума с заданной точностью .

Рассмотрим алгоритм поиска минимума по шагам:

1. Положим i=0, a_i=a, b_i=b причем , а .

2. Вычислим и .

3. Если , то поиск закончен и следует перейти к шагу 4.

4. Если , то положить a_i+1=с, b_i+1=b_i, i=i+1 и перейти к шагу 2.

Если , то положить b_i+1=с, a_i+1=a_i, i=i+1 и перейти к шагу 2.

5. Вычислить и .

Поскольку на каждой итерации отрезок унимодальности сокращается в два раза, то очевидно, что после некоторой n-й итерации длина отрезка [a;b] вычисляется как . Однако этот метод имеет существенный недостаток - вычисление производной от целевой функции.

Пример 7.5-1. Выполнить две итерации по нахождению минимума функции методом средней точки, если минимум отделен на отрезке [1;5].

1-я итерация:

1. a₀=1, b₀=5, , и .

2. 

3. , следовательно, a₁=a₀=1; b₁=c=3.

2-я итерация:

2. 

3. , следовательно, a₂=a₁=1; b₂=c=2.