3.4. Сплайн – интерполяция

В последние годы интенсивно развивается новый раздел современной вычислительной математики – теория сплайнов. Сплайны позволяют эффективно решать задачи обработки экспериментальных зависимостей между параметрами, имеющими достаточно сложную структуру.

Рассмотренные выше методы локальной интерполяции, по существу, являются простейшими сплайнами первой степени (для линейной интерполяции) и второй степени (для квадратичной интерполяции). Наиболее широкое практическое применение, в силу их простоты, нашли кубические сплайны.

Сплайн – это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.

Пусть интерполируемая функция f(x)задана своими значениями y_i, в узлах х_i, (i = 0, 1,..., n). Кубический сплайн на каждом из частичных отрезков [х_i-1;х_i] представляется в виде:

(3.4-1)

где — четверка неизвестных коэффициентов, вычисляемых численными методами [6].

Тема 4. Аппроксимация функций

4.1. Постановка задачи аппроксимации

Замена таблично заданной функции f(x) интерполяционными многочленами на практике не всегда рациональна. Так, например, если для получения интерполирующего полинома требуется использовать100 узлов, то его степень будет равна 99 (на единицу меньше числа узлов). Или значения функции в узлах получены со значительной погрешностью, то добиваться выполнения основного условия интерполяции - совпадения значений функции и интерполяционного многочлена в узлах интерполяции - теряет смысл. В таких случаях принято решать задачу не интерполяции, а аппроксимации функции.

Задача аппроксимации (приближения) функции заключается в замене некоторой функции y=f(x) другой функцией g(x, a₀, a₁, ..., a_n) таким образом, чтобы отклонение g(x, a₀, a₁, ..., a_n) от f(x) удовлетворяло в некоторой области (на множестве Х) определённому условию.

Подбор эмпирических формул состоит из двух этапов – выбора вида формулы и определения содержащихся в ней коэффициентов.

Если неизвестен вид аппроксимирующей зависимости, то в качестве эмпирической формулы обычно выбирают один из известных видов функций: алгебраический многочлен, показательную, логарифмическую или другую функцию в зависимости от свойств аппроксимируемой функции. Поскольку аппроксимирующая функция, полученная эмпирическим путем, в ходе последующих исследований, как правило, подвергается преобразованиям, то стараются выбирать наиболее простую формулу, удовлетворяющую требованиям точности. Часто в качестве эмпирической формулы выбирают зависимость, описываемую алгебраическим многочленом.

Наиболее распространен способ выбора функции в виде многочлена:

,

где φ(x,a₀,a₁,...,a_n)=a₀φ₀(x)+a₁φ₁(x)+...+a_mφ_m(x), аφ₀(x), φ₁(x),...,φ_m(x) – базисные функции (m-степень аппроксимирующего полинома).

На рис. 4.1-1 показана аппроксимация таблично заданной функции алгебраическим многочленом 1-й и 2-й степени.

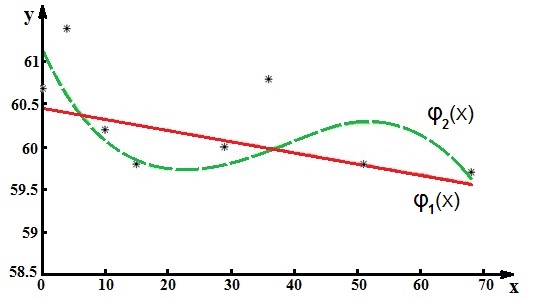
Рис. 4.1-1.

Задача построения аппроксимирующей функции – нахождение коэффициентов полинома (a₀,a₁,...,a_n).

Один из возможных базисов – степенной: φ₀(x)=1, φ₁(x)=х, ..., φ_m(x)=х^m.

Обычно степень аппроксимирующего полинома m<<n, a^T=(a₀,a₁,...,a_m) – вектор коэффициентов. Отклонения между опытными данными и значениями эмпирической функции

e_i = φ(x_i, a₀, a₁, ..., a_m)–y_i, i=0,1,2,...,n.

Методы определения коэффициентов выбранной эмпирической функции различаются критерием минимизации отклонений. Одним из наиболее распространенных методов аппроксимации функции является метод наименьших квадратов.