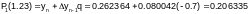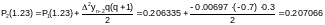3.3.3. Вторая интерполяционная формула Ньютона

Вторая формула Ньютона обладает аналогичными свойствами относительно левой части таблицы. Для ее построения используют многочлен вида:

P_n(x)=a₀+a₁(x-x_n)+a₂(x-x_n)(x-x_n-1)+…+a_n(x-x_n)(x-x_n-1)…(x-x₁), (3.3-8)

где а_i (i =0, 1, 2, …, n) – коэффициенты, не зависящие от узлов интерполяции.

Для определения коэффициентов а_i будем в (3.3-8) поочередно подставлять узлы интерполяции. При х = x_n P_n(x_n)=y_n, следовательно, a₀ = y_n.

При х = x_n-1 имеем P_n(x_n-1) = y_n-1 =a₀+a₁(x_n-1-x_n)=y_n+a₁(x_n-1-x_n), откуда

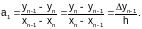
Продолжая подстановку, получим выражение для всех коэффициентов многочлена (3.3-8) и запишем вторую интерполяционную формулу Ньютона:

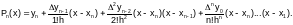(3.3-9)

_{Введя обозначение:}

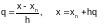
Подставив х в (3.3-8), получаем формулу Ньютона для интерполяции назад:

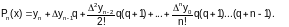(3.3-10)

Воспользуемся этой формулой для вычисления значения функции, заданной табл. 3.3-1, в точке х = 1.7.

Точка х=1.7 расположена в конце таблицы. В качестве узлов интерполяции выберем: х₃=1.8, х₂=1.6 и х₁=1.4:

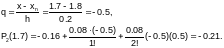
Погрешности интерполяционных формул Ньютона определяются соотношением:

• для первой формулы Ньютона:

(3.3-11)

• для второй формулы Ньютона:

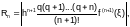(3.3-12)

где 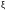- некоторое промежуточное значение между узлами интерполяции.

На практике, если интерполируемая функция y =f(x) задана таблично, полагая, что Dⁿ⁺¹ постоянны, а h – достаточно мало, используют приближенные равенства:

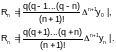(3.3-13)

Пример 3.3-1.Вычислить c использованием 1-й и 2-й формул Ньютона значение функции, заданной таблицей равноотстоящих узлов, в точке х=1.23.

Таблица 3.3-1

x	1.0	1.1	1.2	1.3	1.4
y	0.000000	0.095310	0.182322	0.262364	0.336472

Используем 1-ю формулу Ньютона. Выберем х₀=1.2; х₁=1.3; х₂=1.4.

Построим таблицу конечных разностей:

Таблица 3.3-2

x	y	Dy	D2y
1.2 1.3 1.4	0.182322 0.262354 0.336472	0.080042 0.074108	-0.005934

Тогда:

Практическая погрешность оценивается соотношением:

e₁ = |Р₂(х)-Р₁(х)|=|0.206958-0.206335|=0.000623.

Решим ту же задачу с помощью 2-й формулы Ньютона. Пусть х_n=1.3; х_n-1=1.2; х_n-2=1.1.

Таблица конечных разностей имеет вид:

Таблица 3.3-3

x	y	Dy	D2y
1.1 1.2 1.3	0.095310 0.182322 0.262364	0.087012 0.080042	-0.006970

_Тогда: