Расчет показателей вариации
|
Процент брака,
% ( |
Варианта ( |
Выполненный объем работ, тыс.
деталей ( |
|
|
|
|
0,5–1,0 |
0,75 |
100 |
75 |
1,37 |
137,00 |
|
1,0–1,5 |
1,25 |
120 |
150 |
0,45 |
53,94 |
|
1,5–2,0 |
1,75 |
200 |
350 |
0,03 |
5,81 |
|
2,0–2,5 |
2,25 |
300 |
675 |
0,11 |
32,58 |
|
2,5–3,0 |
2,75 |
160 |
440 |
0,69 |
110,10 |
|
Итого |
|
880 |
1690 |
|
339,43 |
)
)
)
Для расчета среднего процента брака по предприятиям используем формулу средней взвешенной арифметической:
%.
Дисперсия
.
Среднеквадратическое отклонение
%.
Коэффициент вариации
или
32,35%
Таким образом, исследуемая совокупность является однородной, т.к. коэффициент вариации составляет 32,35%. В среднем по исследуемой совокупности варианты отличаются от средней арифметической на 0,6210%.
В статистике наряду с показателями
вариации количественного признака
определяются показатели вариации
альтернативного признака. Альтернативными
являются признаки, которыми обладают
одни единицы изучаемой совокупности и
не обладают другие. Например, продукция
стандартная или нестандартная. Обозначая
наличие признака 1, а отсутствие – 0 и
долю вариантов, обладающих данным
признаком –
,
а долю вариантов, не обладающих им –
и замечая, что
,
получим сначала среднюю:
,
а затем дисперсию альтернативного признака:
Среднее квадратическое отклонение альтернативного признака вычисляется по формуле:
.
Пример. Из 1000 проверенных деталей 3 детали оказались бракованными. Рассчитать показатели вариации.
Доля (частость) бракованных деталей составит:
.
Дисперсия равна:
.
Среднее квадратическое отклонение равно
.
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами, например уровень заработной платы от тарифного разряда рабочих. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсий: общей, межгрупповой и групповой.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих вариацию:
,
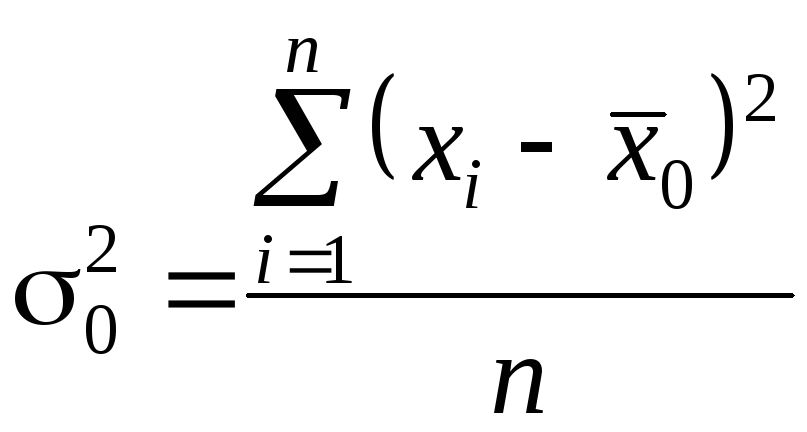где
– общая средняя для всей изучаемой
совокупности,
– численность изучаемой совокупности.
Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она рассчитывается по формуле:
,
где
– средняя поi-ой
группе;
– численность поi-ой
группе.
Внутригрупповая дисперсия отражает случайную вариацию, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки:
.
Средняя из внутригрупповых дисперсий:
.
Общая дисперсия равна сумме из средней внутригрупповой и межгрупповой дисперсий:
.
Данное соотношение называют правилом сложения дисперсий. Это правило сложения дисперсий имеет большую практическую значимость, так как позволяет выявить зависимость результатов от определяющих факторов соотношением межгрупповой и общей дисперсии (коэффициент детерминации):
.
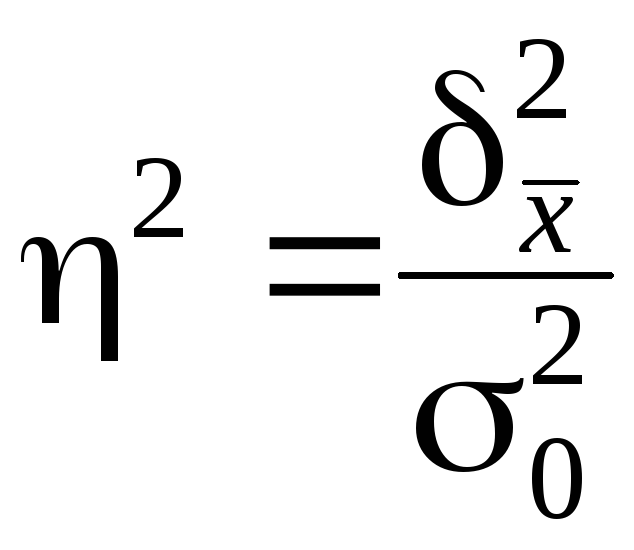Пример. Имеются следующие данные о результатах обследования рабочих предприятия по размеру месячной заработной платы (табл. 6.5).
Т а б л и ц а 6.5
|
Группы рабочих по возрасту, лет |
Число рабочих |
Дисперсия заработной платы |
|
До 20 |
100 |
300 |
|
20 – 30 |
120 |
400 |
|
30 и старше |
150 |
500 |
Общая дисперсия заработной платы в обследованной совокупности рабочих составила 450.
Определить, в какой степени вариация заработной платы рабочих предприятия зависит от возраста.
Средняя внутригрупповая дисперсия характеризует случайную вариацию под влиянием неучтенных факторов:
=
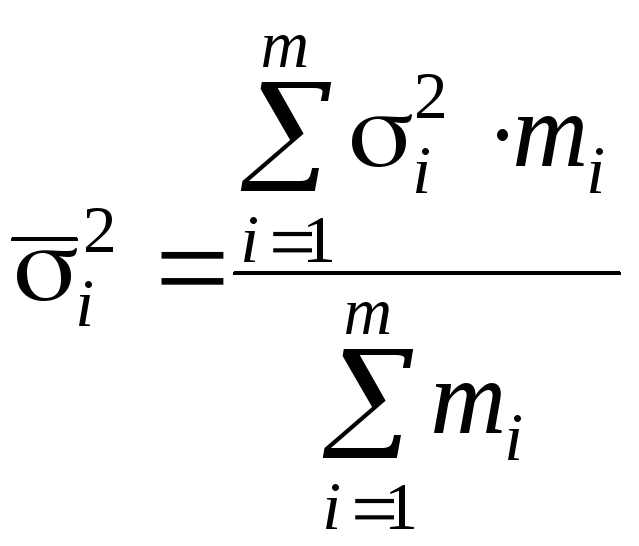Межгрупповая дисперсия отражает систематическую вариацию под влиянием фактора, положенного в основу группировки (возраста рабочих).
Межгрупповая дисперсия определяется по правилу сложения дисперсий:
=
450 – 413,5 = 36,5.
Отсюда соотношение дисперсий
=
36,5: 450 = 0,08, или 8,0%.
Полученный результат показывает, что возраст на варьирование заработной платы рабочих предприятия не оказывает существенного влияния.