Определение темпов роста перевозок грузов

Порядковый номер года, i	Годы	Объем перевозок, млн. т	Темпы роста, %		Средний темп роста,
			цепные	базисные
1	1991	43	-	-	1,058
2	1992	49	113,95	113,95
3	1993	44	89,80	102,33
4	1994	46	104,55	106,98
5	1995	50	108,70	116,28
6	1996	55	110,00	127,91
7	1997	59	107,27	137,21
8	1998	62	105,08	144,19
9	1999	66	106,45	153,49
10	2000	71	107,58	165,12
11	2001	74	104,23	172,09
12	2002	82	110,81	190,70
13	2003	89	108,54	206,98
14	2004	91	102,25	211,63
15	2005	95	104,40	220,93
16	2006	101
17	2007	106
18	2008	113
19	2009	119
20	2010	126

2.2. Прогнозирование грузовых перевозок на основе экстраполяции тренда

2.2.1. Аналитическое выравнивание временного ряда

При аналитическом выравнивании временного ряда теоретические (расчетные) значения ряда определяют исходя из предположения об их зависимости от времени, т.е. .

Основная задача состоит в выборе наилучшей формы тренда, выражающей сущность изучаемого процесса, в расчете неизвестных параметров уравнения тренда.

Тренд – это основная тенденция развития явления во времени, некоторое общее направление развития.

На рис. 1 приведено аналитическое выравнивание временного ряда по уравнению прямой.

Для аналитического выравнивания временного ряда могут использоваться разнообразные формы тренда, поэтому самостоятельной задачей является определение вида функциональной зависимости , наилучшим образом описывающей исходный временной ряд. Существуют специальные способы определения наилучшей формы тренда. В курсовой работе используется так называемый критериальный способ, т.е. наилучшая форма тренда определяется на основе системы статистических критериев.

Рис. 1. Выравнивание временного ряда по уравнению прямой

В качестве уравнений тренда в курсовой работе использованы:

а) уравнение прямой: ;

б) уравнение параболы ;

в) уравнение показательной функции.

Параметры а, b, с определяются методом наименьших квадратов.

При выравнивании по прямой, для нахождения параметров a и b используется система нормальных уравнений, имеющая вид:

Нахождение параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого временного ряда была равна нулю:

.

При нечетном числе уровней ряда динамики для получения уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (нулевое значение). Даты времени, стоящие выше этого уровня, будут обозначаться натуральными числами со знаком минус (–1, –2, –3 и т.д.), а ниже – натуральными числами со знаком плюс (+1, +2, +3 и т.д.).

В этом случае будет равна нулю, и система нормальных уравнений будет преобразована следующим образом:

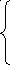
Откуда,

; .

Расчеты, необходимые для нахождения параметров прямой при выравнивании фактических уровней временного ряда сводятся в табл. 2.

Используя итоги граф 4, 5 и 6 определяются параметры уравнения прямой a и b и рассчитываются выравненные уровни ряда – графа 7.

В графе 8 определяется ошибка ε – отклонение фактических уровней временного ряда от теоретических (точек на тренде) по следующей формуле:

.

Итоговые значения граф 9 и 10 будут использованы при расчете статистических критериев.

Необходимо изобразить на графике фактические и выравненные по уравнению прямой уровни ряда (см. в качестве примера рис. 1).

Параметры a, b и c уравнения параболы 2-го порядка определяются по формулам (при = 0):

;

; .

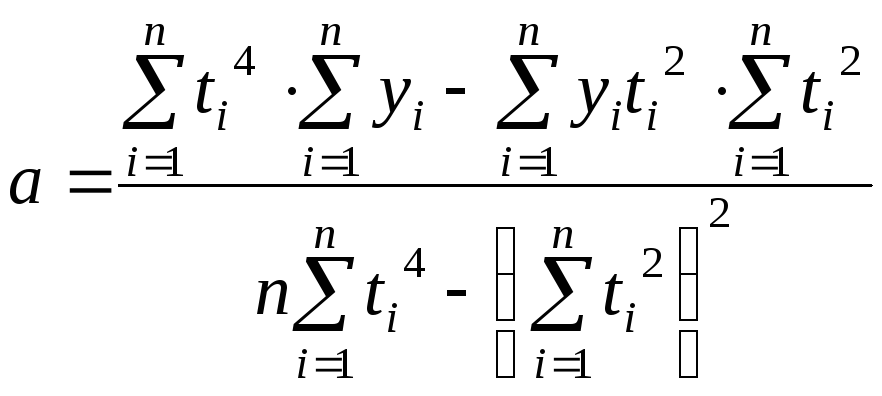Рис.4 Фактические и выравненные (теоретические) по уравнению прямой уровни ряда объемов перевозок (млн. т.)

Расчеты, необходимые для нахождения параметров параболы при выравнивании фактических уровней временного ряда, сводятся в табл. 3.

Используя итоги граф 4, 5, 6, 7 и 8, необходимо определить параметры уравнения параболы a, b и с и рассчитать выравненные уровни ряда – графа 9. Далее изобразить на графике фактические и выравненные по уравнению параболы уровни ряда.