Применение excel при решении математических и физических задач. Оптимизация данных

Для решения всевозможных математических, вычислительных и физических задач EXCELрасполагает, во-первых: большим набором встроенных математических и тригонометрических функций, во-вторых: набором инструментов для поиска решения и развитым аппаратом численного анализа данных. Встроенные функции доступны черезмастер функций, инструменты через менюСервис. Далее приведены методы решения некоторых математических и физических задач

Табулирование функции одной переменной и построение её графика.

Табулирование функции – это вычисление значений функции на заданном отрезке значений аргумента. Т. е. X[Xn,Xn+Dx,Xn+2Dx,…Xk] (Dx-шаг приращения аргумента) и задана формула для вычисленияF(X). ПолучитьNзначений функции, где. ВEXCELэта задача выполняется легко, применяя автозаполнение. Задайте значенияXn,XkиDx.

Т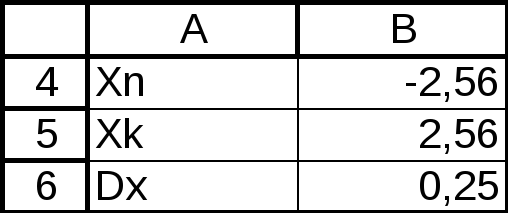аблица значений аргумента и функции

Вячейку А8 записывается формулаXn(В4), в А9 :X(А8)+Dx(В6), далееавтозаполнениеячеек, копируемая ячейка - А9. Аналогично в ячейку В8 записывается формула для вычисления функции, а далее выполняетсяавтозаполнение.Получаем таблицу значений аргумента и функции. Ссылка на ячейку В6 имеет абсолютный адрес, т. к. при копировании он не должен изменяться (приращениеDxостаётся без изменений).

Построение графика функции

Запустите мастер диаграмм. На первом шаге выбираем вид диаграммы – непрерывный график. На втором указываем диапазон значений функции( в нашем примере В8:В28). Перейдите на вкладку Ряди в окнеПодписи оси Xукажите диапазон А8:А28. В окнеИмяУкажите ячейку В7. Нажмите кнопкуДалее. На третьем шаге укажите параметры диаграммы: На вкладкеЗаголовки: В окнеНазвание диаграммынаберитеГрафик функции SinX +CosX,в окнеОсь Хнаберите Х, в окнеОсь Y-F(X). Нажмите кнопку Далее. На четвёртом шаге укажите, что диаграмму строить на имеющемся листе.

Аппроксимация функций

Значения функции, полученные методом табулирования не отражают истинное поведение функции на заданном отрезке. Это так называемый табличный метод задания функции. В этом случае нет информации о значениях функции между точками XиX+Dx. Для более точного описания процесса(физического, химического и т.д.) применяют аппроксимацию или интерполяцию функции.Excelрасполагает средствами, позволяющими прогнозировать процессы.

Аналитическая функция называется трендоми может иметь разный вид и разный уровень сложности в зависимости от желаемой точности представления.

С помощью средств Excelможно получить линии тренда и соответствующие им уравнения. Самой простой является линейная аппроксимирующая функцияAx+B, но при этом погрешность аппроксимации бывает очень большой. Можно выбрать экспоненциальное приближениеA e ^Bx. , но наиболее точным является полиномиальное приближениеAxⁿ+Bx^n-1+Cx^n-2+…+Z и чем выше степень полинома, тем меньше погрешность аппроксимации.

Чтобы получить линии тренда, щёлкните на графике функции правой кнопкой мыши. В появившемся контекстном меню выберите пункт Добавить линию тренда, который предъявляет окноЛиния тренда. Здесь можно выбрать вид уравнения аппроксимации и его степень. Если во вкладке Параметры установить флагПоказывать уравнение на диаграмме, то на графике мы увидим не только линию тренда, но и его уравнение. Здесь же можно визуально оценить поведение анализируемого процесса в будущем/прошлом, если установитьПрогноз вперёд/назадна заданное число единиц независимого аргументаX.

Построим линии тренда для нашего примера.

На график добавлены три линии тренда :линейная , логарифмическая и полиномиальная. Достоверность аппроксимации характеризуется коэффициентом корреляцииR. Принято считать, что приR<0,3 наблюдается слабая связь, приR=1 –полная функциональная связь. Из графика видно, что полиномиальное приближение наиболее достоверно. Чтобы показать коэффициент достоверности на графике, установите соответствующий флажок на вкладкеПараметрыпри выполнении опцииДобавить линии тренда

Для получения коэффициентов линейной регрессии в EXCELесть встроенная функция ЛИНЕЙН(<известноеY>;<известноеX>). Напомним вид уравнения линейной регрессииAx+B. Коэффициент А вычисляется по формуле ИНДЕКС(ЛИНЕЙН(<массив значений функции>;<массив значений аргумента>);1), аB= ИНДЕКС(ЛИНЕЙН(<массив значений функции>;<массив значений аргумента>);2).Функция ЛГРФПРИБЛ() возвращает коэффициенты логарифмического приближения АВ^х. Применение формулы аналогично .

Для нашего примера

.Для сравнения , какие из них более точные, подсчитаем среднее отклонение и дисперсию отклонения.

Врежиме значений

Видим, что коэффициенты, полученные с использованием функции ЛИНЕЙН() устанавливают более точную функциональную связь.