Konspekt_lektsy_po_inzhenernoy_grafike

90º к линиям связи.

На рис. 1.33 представлен рисунок пирамиды SABCDE, грани которой по отношению к плоскостям проекций занимают разные положения: ABCD – горизонтальная грань; SAE – фронтальная грань; SED – профильная грань; SAB – фронтально-проецирующая грань; SCD – профильно-проецирующая грань; SBC – грань общего положения. Пирамида SABCDЕ не содержит лишь горизонтально-проецирующую грань. Такая плоскость, заданная прямоугольником, показана на рис. 1. 34.

Особенностью плоскостей особого положения есть то, что кроме представленных на черт. 1.32 способов задания на чертеже, они могут быть представлены лишь одной линией – следом-проекцией с пометкой плоскости – прописной греческой буквы и индекса плоскости проекций, на которой они изображены.

Следует отметить важное свойство плоскостей особого положения. Все

точки, линии или плоские фигуры, расположенные в плоскости особого положения, проецируются на след-проекцию этой плоскости (собира-

тельное свойство).

23

Продолжение табл. 2

В таблице 2 приведены плоскости особого и общего положения, по форме подобные изображенным на рис. 1.33 и рис. 1.34.

◊ Как называются представленные на рисунке плоскости?

24

вращения, называется меридианом. Фронтальный меридиан называют

26

прямой или кривой, но всегда стремятся к тому, чтобы эта линия была наиболее простоя (прямая, окружность).

Рассмотрим построение ряда точек на поверхностях. На всех чертежах заданы фронтальные проекции точек, которые лежат на видимой части поверхности. Если точка лежит на линии, которая задает поверхность, построение ее сводится к нахождению этой линии на другой проекции и фиксации линией связи отсутствующей проекции точки (рис. 1.35, а точка К).

На поверхностях вращения эта задача немного отличается, так как крайняя очерковая линия на одной проекции не является таковой на другой (рис. 1.36, точка К). В особенности это характерно для сферы и тора, где на главном виде очерковой линией служит главный меридиан, а на виде сверху

– экватор (для тора еще и горло) (рис. 1.38, 1.39, точки К и L).

Среди представленных поверхностей лишь призматические и цилиндрические поверхности при определенных условиях могут быть проецирую-

щими. В таком случае, любая точка, которая лежит на их боковой поверхности, проецируется на след-проекцию (рис. 1.35, б, рис. 1.37, точка Н).

На рис. 1.35, а для построения точки G на виде сверху взята произвольная прямая линия.

На конической поверхности (рис. 1.36) для построения горизонтальной проекции точки М проведена образующая 1S, а для точки N – окружность, которая расположена горизонтально.

На сфере (рис. 1.38) для построения точек использованы окружности: одна из семейства, расположенных параллельно экватору (точка М), а вторая

– меридиану (точка N).

На торе (рис. 1.39) существует семейство окружностей, параллельных его экватору. С помощью одной из них построена точка N.

◊Как получают поверхности вращения?

◊Как построить точку, которая принадлежит поверхности?

◊Постройте отсутствующие проекции точек К и L, которые принадлежат, соответственно, граням АВFD и ВСFЕ. Постройте проекции ломаной

27

28

◊Как строится линия сечения поверхности плоскостью?

◊Какие линии могут быть получены при пересечении цилиндрической, конической и сферической поверхностей плоскостями?

29

РАЗДЕЛ 2 ЧЕРТЕЖИ МОДЕЛЕЙ

В результате изучения раздела студент должен уметь представлять в пространстве и изображать на чертежах геометрические тела и их соединения, а так же наносить необходимые размеры.

2.1 Геометрические тела

Геометрическим телом называют часть пространства ограниченного совокупностью поверхностей и плоскостей. Необходимым условием существования геометрического тела является отсутствие разрывов между образующими это тело элементами. Считается, что геометрические тела заполнены некоторым материалом, поэтому, при условных рассечениях их принято штриховать, как штрихуют металл – тонкими сплошными линиями с наклоном влево или вправо под углом 45к горизонту.

Среди геометрических тел есть многогранники, ограниченные только плоскими многоугольниками, а так же большое количество других видов тел, поверхность которых включают как поверхности, так и плоскости в разных соединениях. Имеются поверхности, которые без каких-нибудь дополнений относятся к геометрическим телам, так как они ограничивают некоторый объем пространства. Самые известные – сфера, тор, эллипсоид вращения и т.п.

Типичными представителями многогранников, в основе которых лежат пирамидальные и призматические поверхности, являются пирамиды и призмы.

Пирамида – многогранник, в основании которого лежит многоугольник, а боковые грани – треугольники с общей вершиной.

Призма – многогранник, у которого основания – два одинаковых и взаимно параллельных многоугольника, а боковые грани – параллелограммы. Если ребра призмы располагаются перпендикулярные плоскостям основания, то ее называют прямой, если нет, то – наклонной.

Плоскости, которые создают многогранник, пересекаясь между собой, дают ребра и вершины многогранника. Совокупность ребер и вершин называют сеткой многогранника. Изображение многогранника на чертеже сводится к изображению его сетки.

Геометрические тела, которые включают поверхности, изображаются на чертеже крайними (очерковыми) линиями. Если это поверхность вращения, то на ее изображениях обязательно должны присутствовать проекции осей вращения.

30

Прямые круговые цилиндр и конус получают из соответствующих поверхностей вращения с привлечением плоскостей, перпендикулярных осям вращения. Эти плоскости носят название оснований. Цилиндр имеет два основания, а конус – одно основание и вершину. Усеченный конус имеет два

основания.

Для пояснения формы отдельных элементов детали на производственных чертежах широко используются сечения. Сечением называют изобра-

жение фигуры, получаемой при мысленном рассечении предмета одной или несколькими плоскостями.

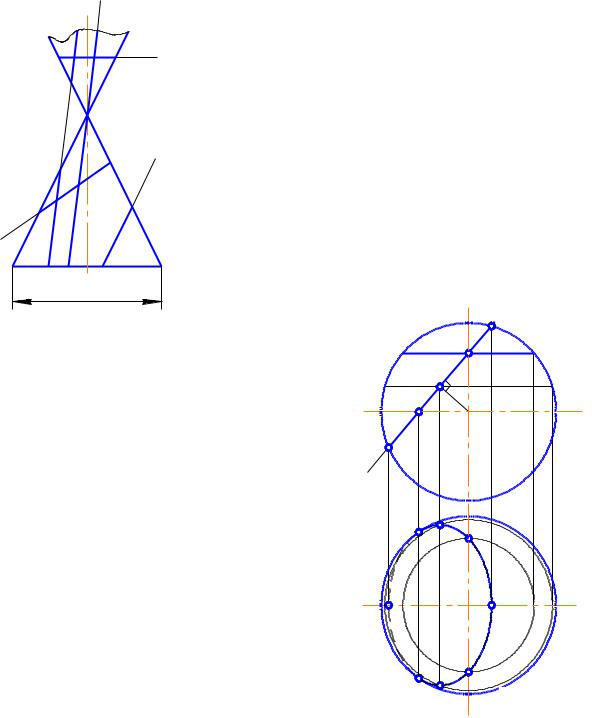
При построении сечений геометрических тел плоскостями получают замкнутую плоскую фигуру. На рис. 2.1 показано построение линии сечения прямого кругового конуса с фронтальным основанием горизонтальнопроецирующей плоскостью. Попутно введем обозначение расположения сле- дов-проекций секущей плоскости, принятое на производственных чертежах. Это два штриха разомкнутой линии и стрелки, расположенные перпендикулярно этим штрихам, указывающие направление взгляда при проецировании. Обозначают секущую плоскость, а также полученное сечение, прописными буквами русского алфавита. Независимо от расположения секущей плоскости эти буквы всегда располагают горизонтально.

Сечение в данном случае представляет плоскую замкнутую фигуру, ограниченную частью эллипса и отрезком прямой. Он построен с помощью опорных точек, которые принадлежат секущей плоскости, поверхности конуса и плоскости его основания. Для удобства построений взята точка 2. Она не

31

принадлежит сечению, но определяет величину большой оси эллипса. Малая ось (3, 4) располагается посередине большой оси под углом 90º к ней. Измерение высотных координат для построения точек на сечении проводилось от горизонтальной оси симметрии фронтальной проекции конуса.

Сечение может быть повернутым относительно расположения секущей плоскости. Повернуть его можно на угол меньший 90º, так чтобы ось располагалась горизонтально. Обозначение сечения при этом сопровождается особым значком (см. рис. 2.1).

2.2 Выбор изображений на чертеже

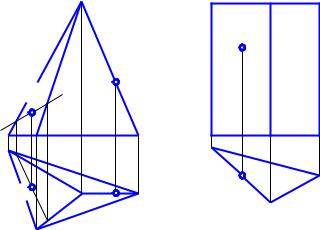
Используя аппарат проектирования, можно назначить любые направления взгляда на предмет и получить в общем случае неограниченное количество его изображений. Какие из этих изображений необходимы для создания чертежа? Каким их количеством надо ограничится? Решение этих вопросов представляет серьезную проблему. Сущность ее рассмотрим на примере. На рис. 2.2 приведены два варианта изображений многогранника. По этим изображениям можно однозначно установить его форму – пирамида, в основании которой лежит правильный треугольник. Есть возможность нанести размеры высоты и диаметра окружности, описанной вокруг основания. Этих размеров достаточно для построения изображений пирамиды и варианты можно считать равноценными. Студенты, при обсуждении темы, часто отдают предпочтение чертежу (рис. 2.2, б), мотивируя тем, что изображения на нем содержат большее количество линий. Очевидно, здесь без внимания остается главный вопрос: для чего предназначены чертежи?

32